פונקציית הערך השלם

מתוך ויקיפדיה, האנציקלופדיה החופשית

הגרף של פונקציית הערך השלם

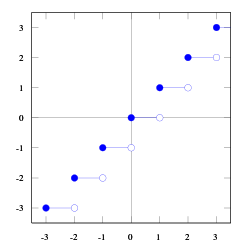
במתמטיקה, פונקציית הערך השלם (נקראת גם פונקציית רצפה) היא פונקציה המחזירה לכל מספר ממשי x את המספר השלם הגדול ביותר שקטן או שווה ל-x. פונקציה זו מסומנת $\lfloor x \rfloor$ או (x)‏floor (בספרים ישנים נפוץ הסימון $\ [x]$ ). דוגמאות: $\lfloor 2.7 \rfloor = 2$ , $\lfloor -2.1 \rfloor = -3$ , $\lfloor -2 \rfloor = -2$ .

[עריכה] תכונות

לכל x ממשי הפונקציה מקיימת:

$\lfloor x \rfloor \le x < \lfloor x \rfloor +1$

כאשר השוויון באגף שמאל מתקיים אם ורק אם x שלם.

הפונקציה היא אידמפוטנטית: $\lfloor \lfloor x \rfloor \rfloor = \lfloor x \rfloor$
לכל x ממשי ולכל n שלם מתקיים:

$\lfloor x + n \rfloor = \lfloor x \rfloor + n$

עיגול למספר השלם הקרוב ביותר ל-x ניתן על ידי הנוסחה $\lfloor x + 0.5 \rfloor$ .
אם m ו-n זרים זה לזה, אזי מתקיים:

$\sum_{i=1}^{n-1} \lfloor im / n \rfloor = (m - 1) (n - 1) / 2$

[עריכה] פונקציית תקרה

הגרף של פונקציית תקרה

פונקציית התקרה מחזירה לכל מספר ממשי x את המספר השלם הקטן ביותר שגדול או שווה ל-x. הפונקציה מסומנת $\lceil x \rceil$ או (x)‏ceiling. דוגמאות: $\lceil 2.7 \rceil = 3$ , $\lceil -2.1 \rceil = -2$ , $\lceil -2 \rceil = -2$ .