קיבול
קיבול הוא תכונה פיזיקלית המתארת את היכולת של גוף (לרוב שניים) לאגור מטען חשמלי. הקיבול, , מוגדר כיחס בין המטען האגור בגוף, , לבין הפרש הפוטנציאל עליו, :
במערכת היחידות הבינלאומית, קיבול נמדד ביחידת המידה פאראד, על שמו של מייקל פארדיי, ומסומלת באות . זוהי יחידת מידה גדולה יחסית והיא מציינת גוף הטעון ב-1 קולון ליחידת הפרש פוטנציאלים של 1 וולט.[1] השגת קיבול גבוה היא אתגר המצריך לרב הגדלה של נפח הגוף כי הקיבול תלוי בפרמטרים הגאומטריים של הקבל, ובתכונות החומרים המרכיבים אותו, אך לא במטען שהוא מכיל.
קבל[עריכת קוד מקור | עריכה]
 ערך מורחב – קבל
ערך מורחב – קבל

קבל הוא רכיב חשמלי בעל יכולת לאגור מטען חשמלי ולפרוק אותו. קבל בנוי משני מוליכים המופרדים על ידי מבודד. כאשר הקבל "טעון", על שני ההדקים שלו יש מטען השווה בגודלו והפוך בסימנו, כך שבין ההדקים נוצר שדה חשמלי. סך המטען על קבל הוא תמיד 0. תאורטית, כל זוג מוליכים (ואפילו מוליך יחיד) יכולים לתפקד כקבל, אך הסוגים הנפוצים ביותר הם קבל לוחות וקבל קואקסיאלי.
קיבול של מערכות פשוטות[עריכת קוד מקור | עריכה]
חישוב קיבולה של מערכת מבוסס על פתרון משוואת לפלס, כאשר , כאשר, , הפוטנציאל על פני השטח של מוליכים טעונים קבוע. פתרון זה טריביאלי עבור מקרים בעלי סימטריה גבוהה, אך אין בהכרח פתרון בעזרת פונקציות יסודיות במקרים מסובכים יותר.
| סוג | קיבול | הערות |
|---|---|---|
| קבל לוחות | ||
| קבל קואקסיאלי | 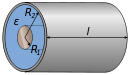
| |
| זוג כבלים מקבילים | 
| |
| כבל מקביל ללוח | : רדיוס הכבל : מרחק, : אורך הכבל | |
| ספרות קונצנטריות | 
| |
| זוג ספרות בעלות רדיוס זהה | : רדיוס : מרחק, = : קבוע אוילר | |
| ספרה ולוח | : רדיוס : מרחק, | |
| ספרה | : רדיוס | |
| דיסק עגול | : רדיוס | |
| כבל דק באורך סופי | : רדיוס הכבל : אורך |
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- קיבול, באתר אנציקלופדיה בריטניקה (באנגלית)
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ הגדרת פאראד במילון Collins






























![{\displaystyle {\frac {2\pi \varepsilon l}{\Lambda }}\left\{1+{\frac {1}{\Lambda }}\left(1-\ln 2\right)+{\frac {1}{\Lambda ^{2}}}\left[1+\left(1-\ln 2\right)^{2}-{\frac {\pi ^{2}}{12}}\right]+O\left({\frac {1}{\Lambda ^{3}}}\right)\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8d4d56c633ce773c15c52403b1f8c185a95bbbbc)
