לוגיקת זמן

לוגיקת זמן, או לוגיקה טמפורלית (באנגלית: Temporal Logic) היא הרחבה של הלוגיקה הקלאסית המאפשרת ביטויים הקשורים בזמן. לוגיקת זמן היא חלק מהלוגיקה המודלית.

לוגיקת זמן מאפשרת לנו לעסוק בקו זמן, ועל כן מאפשרת לנו לנסח מתמטית משפטים כמו "אני תמיד רעב", "לבסוף אהיה רעב", או "אהיה רעב עד שאוכל משהו". קו הזמן מתחלק לשני סוגים אפשריים: קו זמן לינארי, שמוגבל לקו זמן אפשרי אחד (כמו בדוגמאות לעיל), וקו זמן מסתעף (Branching logic) שמאפשר לעבוד במספר קוי זמן חלופיים במקביל. בצורה כזו אנו מניחים מראש סביבה לא צפויה שמספר דברים שונים יכולים להתרחש בה. בסביבה כזו נוכל לנסח את המשפטים: "יש אפשרות שאשאר רעב לנצח" או "יש אפשרות שלבסוף לא אהיה רעב". במידה ואנו לא יודעים אם אי פעם אוכל - שני המשפטים הם בחזקת נכונים.

אמיר פנואלי זכה בשנת 1996 בפרס טיורינג על הכנסת לוגיקת הזמן אל מדעי המחשב. כיום נעשה שימוש נרחב בלוגיקת זמן באימות תוכנה כדי להוכיח מתמטית נכונות של מערכת מחשב, זאת להבדיל מתהליך בדיקת תוכנה על ידי בודקי תוכנה אנושיים.

אופרטורים של לוגיקת זמן

לוגיקת זמן מכילה שני סוגי אופרטורים: אופרטורים לוגיים ואופרטורים מודליים. האופרטורים הלוגיים הם פעולות בוליאניות רגילות ($\neg,\or,\and,\rightarrow$). האופרטורים המודליים שמתשמשים בהם בלוגיקת זמן מוגדרים כך:

טקסטואלי	סימול	הגדרה	הסבר	תרשים
אופרטורים בינארים
$\phi$ U $\psi$	$\phi ~\mathcal{U}~ \psi$	$\begin{matrix}(B\,\mathcal{U}\,C)(\phi)= \\ (\exists i:C(\phi_i)\land(\forall j<i:B(\phi_j)))\end{matrix}$	$\phi$ מתקיים עד ש- $\psi$ מתקיים: $\psi$ מתקיים בנקודת הזמן הנוכחית או בנקודת זמן עתידית, ועד נקודת זמן זו $\phi$ חייב להתקיים. מנקודת הזמן בה $\psi$ מתקיים, $\phi$ כבר לא חייב להתקיים.
$\phi$ R $\psi$	$\phi ~\mathcal{R}~ \psi$	$\begin{matrix}(B\,\mathcal{R}\,C)(\phi)= \\ (\forall i:C(\phi_i)\lor(\exists j<i:B(\phi_j)))\end{matrix}$	$\phi$ משחרר את $\psi$ : $\psi$ מתקיים עד נקודת הזמן הראשונה בה $\phi$ מתקיים (ואחרי זה $\psi$ יכול להתקיים או לא להתקיים), או ש- $\psi$ מתקיים לנצח אם $\phi$ לא מתקיים לעולם.
אופרטורים אונריים
N $\phi$	$\circ \phi$	$\mathcal{N}B(\phi_i)=B(\phi_{i+1})$	$\phi$ מתקיים בנקודת הזמן הבאה.
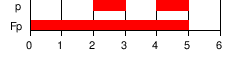
F $\phi$	$\Diamond \phi$	$\mathcal{F}B(\phi)=(true\,\mathcal{U}\,B)(\phi)$	לבסוף: לבסוף $\phi$ מתקיים. כלומר בהכרח קיימת נקודה עתידית שבה $\phi$ מתקיים.
G $\phi$	$\Box \phi$	$\mathcal{G}B(\phi)=\neg\mathcal{F}\neg B(\phi)$	תמיד: $\phi$ תמיד מתקיים.
A $\phi$		$\begin{matrix}(\mathcal{A}B)(\psi)= \\ (\forall \phi:\phi_0=\psi\to B(\phi))\end{matrix}$	$\phi$ מתקיים תמיד בכל נקודות הזמן בכל המסלולים שמתחילים בנקודת זמן זו.
E $\phi$		$\begin{matrix}(\mathcal{E}B)(\psi)= \\ (\exists \phi:\phi_0=\psi\land B(\phi))\end{matrix}$	קיים לפחות מסלול אחד מנקודת זמן זו שבו $\phi$ מתקיים.

סימולים אלטרנטיביים:

• אופרטור R מוחלף לעתים על ידי הסימון V.
• אופרטור W משמעו U חלש ושקול ל- $f U g \or G f$. כלומר $\phi ~\mathcal{W}~ \psi$ משמעו $\phi$ מתקיים עד ש- $\psi$ מתקיים, או ש- $\phi$ ממשיך להתקיים לעולם.

אופרטורים אונריים מוגדרים היטב כאשר (B($\phi$ מוגדר היטב. אופרטורים בינארים מוגדרים היטב כאשר (B($\phi$ ו- (C($\phi$ מוגדרים היטב.

שקילויות

להלן מספר שקילויות בלוגיקת זמן שניתן להסיק מההגדרות שניתנו לעיל:

• $\Box\Box \phi = \Box \phi$
• $\Diamond\Diamond\phi = \Diamond\phi$
• $\phi \rightarrow \Diamond\phi$
• $\Diamond\Box\Diamond\phi = \Box\Diamond\phi$
• $\Box\Diamond\Box\phi = \Diamond\Box\phi$
• $\neg\Box\phi \rightarrow \Diamond\neg\phi$
• $\neg\Diamond\phi \rightarrow \Box\neg\phi$
• $\circ\phi \rightarrow \Diamond\phi$
• $\Diamond\psi \rightarrow \Diamond (\phi ~\mathcal{U}~ \psi)$
• $\Box\phi \or \Box\psi \rightarrow \Box(\phi\or\psi)$
• $\Box\phi \and \Box\psi = \Box(\phi\and\psi)$

ראו גם

• לוגיקה
• לוגיקה מודלית
• אימות תוכנה