מחלק מתח
באלקטרוניקה, מחלק מתח הוא מעגל חשמלי ליניארי ופשוט אשר המתח החשמלי במוצאו (המסומן Vout) הוא רק חלק מהמתח החשמלי במבואו (המסומן Vin). המונח חלוקת מתח מתייחס לאופן שבו, על-פי חוק המתחים של קירכהוף, על כל אחד מרכיבי המעגל החשמלי נופל חלק יחסי מהמתח אשר מוזן למעגל.
שימוש נפוץ במחלק מתח הוא קבלת מתח רצוי במעגל שבו קיימים מקורות מתח קבועים. הדוגמה הפשוטה ביותר למחלק מתח היא חיבור טורי של שני נגדים. נגדים משתנים רבים מכילים 3 הדקים, כאשר 2 הקיצוניות הן קבועות, והאמצעית משתנה בהתאם לכוונון הנגד ומהווה מוצא של מחלק מתח. במעגלי זרם חילופין, מחלקי מתח מתארים הנחתת אותות כתלות בתדירות שלהם.
בזרם ישר[עריכת קוד מקור | עריכה]
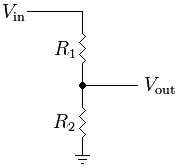
מחלק מתח פשוט מורכב משני נגדים בחיבור טורי בין מקור מתח לבין הארקה. ההתנגדות השקולה של שני הנגדים היא R1+R2. על-פי חוק אוהם, הזרם במעגל הוא:
לכן המתח על הנגד R2, שהוא מתח המוצא, יהיה:
לפיכך, מוצאו של מחלק המתח הוא פי מהמתח במבוא.
לדוגמה, כדי לקבל במוצא מחצית ממתח המבוא, יש להשתמש בשני נגדים בעלי התנגדות זהה:
בזרם חילופין[עריכת קוד מקור | עריכה]

במעגלי זרם חילופין, מתח המוצא מתחלק בין עכבות כלשהן Z1 ו-Z2 שיכולות להיות של נגדים, קבלים וסלילי השראה. במעגל כזה, הקשר בין פאזור המתח לפאזור הזרם במצב סינוסי מתמיד הוא:
אם פאזור מתח המוצא הוא:
ועל ידי הצבת פאזור הזרם:
מתקבל פאזור מתח המוצא כתלות בפאזור מתח המבוא:
פאזור מתח המוצא שווה למכפלת פאזור מתח המבוא בגודל :
הוא גודל מרוכב התלוי בתדירות מקור המתח ונקרא פונקציית התמסורת. המודול של פונקציית התמסורת הוא היחס בין משרעת מתח המוצא למשרעת מתח המבוא. מופע פונקציית התמסורת בהצגה קוטבית הוא הפרש המופע בין המבוא למוצא.
הנוסחאות המתארות מחלק זרם דומות לאלו של מחלק מתח, אך המונה מכיל את גודלה של העכבה שבין המקור למוצא (בניגוד למחלק מתח, בו המונה מכיל את העכבה שבין המוצא להארקה).
דוגמה – מסנן מעביר תדרים נמוכים[עריכת קוד מקור | עריכה]

מעגל RC הוא דוגמה למחלק מתח המורכב מנגד וקבל. כאשר מתח המוצא הוא המתח על הקבל, מעגל זה מתפקד כמסנן המעביר תדרים נמוכים. עכבת הקבל היא:
כאשר הוא הקיבול הקבל, היא היחידה המדומה, ו־ היא התדירות הזוויתית של אות הכניסה.
היחס שנוצר במחלק המתח הוא:
כלומר:
היחס בין פאזור מתח המוצא לפאזור מתח הכניסה תלוי בתדירות אות הכניסה. מאחר שתדר אות הכניסה מופיע במכנה, מתח המוצא יקטן ככל שהתדר יגדל, וזהו למעשה מסנן אשר מעביר תדרים נמוכים ומנחית תדרים גבוהים. מתח קבוע יעבור כמו שהוא למוצא, ובחיבור מקור מתח סינוסי לכניסה, מתח המוצא יהיה סינוסי בתדירות זהה אך במשרעת שתלך ותקטן ככל שהתדירות תגדל.
השפעת העומס[עריכת קוד מקור | עריכה]

המתח שבמוצא המעגל תלוי רק במרכיבי מחלק המתח, אך כאשר מחברים רכיבים נוספים כעומס על המוצא, הם למעשה מתחברים במקביל ל-Z2 ובכך נוצרת עכבה שקולה חדשה שמחוברת כולה בטור אל Z1. לפיכך, כאשר מתכננים מחלק מתח שמיועד להתחבר אליו עומס - יש להתחשב גם בהשפעת עכבת העומס על מתח המוצא.
















