פאזור (אלקטרוניקה)
פאזור (באנגלית: phasor) הוא קבוע מרוכב המייצג פונקציה סינוסואידית של הזמן בעלת משרעת ותדירות קבועה בעזרת האקספוננט המרוכב. פאזורים משמשים בהנדסת חשמל ובפיזיקה על מנת לפשט בעיות הכוללות משוואה דיפרנציאלית לפתרון משוואה אלגברית, או על מנת לפשט בעיות הכוללות חיבור פונקציות סינוסואידיות באותה התדירות לחיבור אלגברי של מספרים מרוכבים.
בחיבור פאזורי באלקטרוניקה התדר של כל הרכיבים במעגל זהה, וההבדל בין הרכיבים הוא במשרעת ובהפרש המופע מהמקור.
הגדרה[עריכת קוד מקור | עריכה]
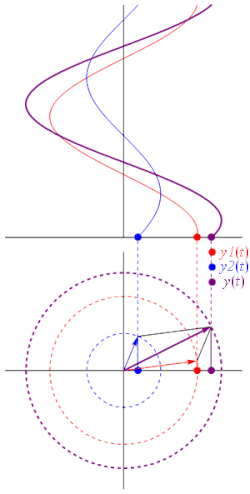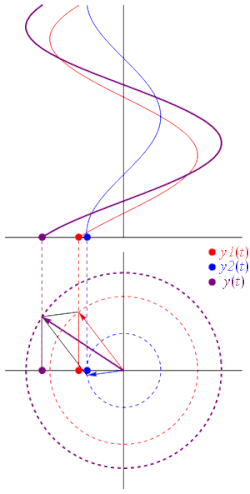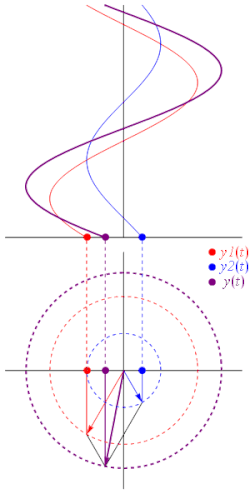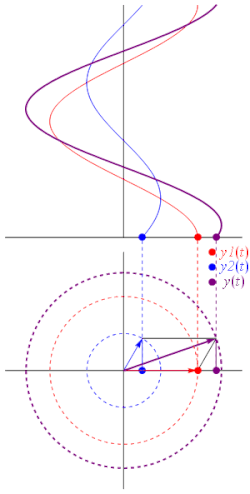
סינוסואידה (או צורת גל סינוסית) היא פונקציה מהצורה:
כאשר:
- המשרעת (השיא) של הפונקציה (מספר ממשי)
- הוא המופע ההתחלתי (לרוב נמדד ברדיאנים)
- היא התדירות הזוויתית ( כאשר היא התדירות בהרץ)
- הוא הזמן
לפי נוסחת אוילר, ניתן לכתוב באופן שקול:
כאשר היא היחידה המדומה ו- הוא החלק הממשי של המספר המרוכב .
הפאזור של מוגדר להיות המשרעת המרוכבת של , ומסומן :
הפאזור הוא קבוע מרוכב שמכיל בתוכו את המשרעת ואת המופע של הסינוסואידה, ולעיתים משתמשים בסימון המפושט של גודל וזווית:
כאשר A הוא גודל הפאזור ו- הזווית מהציר האופקי בהצגה קוטבית של המספר במישור המרוכב. בהנדסת חשמל, המופע מצוין בדרך כלל במעלות במקום ברדיאנים, והגודל ניתן לעיתים על ידי שורש ממוצע הריבועים (ממוצע RMS) במקום על ידי המשרעת.
היתרון בשימוש בפאזורים הוא הקלות הרבה שבה פעולות האריתמטיקה נעשות על מספרים מרוכבים ביחס לפונקציות טריגונומטריות. בהנחה שהתדירות של מספר פונקציות זהה, קל יותר לבצע את פעולות החשבון על הפאזורים ורק לאחר מכן להכפיל באקספוננט המרוכב התלוי בזמן ולקחת את החלק הממשי של התוצאה.
תנאים לשימוש בפאזורים[עריכת קוד מקור | עריכה]
כדי שאפשר יהיה להמיר נתוני מעגל חשמלי לפאזורים, על המעגל לקיים את התנאים להלן:
- יציבות אסימפטוטית – לאחר זמן רב בו המערכת פועלת היא מגיעה למצב יציב. כלומר, הפתרון ההומוגני של המשוואה הדיפרנציאלית של המעגל שואף ל-0 ונשאר רק הפתרון הפרטי שלה.
- הכניסה של מקור המעגל היא פונקציה סינוסואידית (כלומר, צירוף ליניארי של פונקציות מסוג סינוס וקוסינוס).
- המערכת היא ליניארית וקבועה בזמן (LTI) – מכיוון שבמערכות LTI האקספוננט המרוכב הוא פונקציה עצמית של המערכת, משמע שהתדר שנכנס למערכת הוא אותו התדר שיוצא מהמערכת. החיבור הפאזורי מתבסס על העובדה שהתדר של כל תגובות המערכת הוא אותו תדר.
חשבון פאזורי[עריכת קוד מקור | עריכה]
כאשר סינוסואידה מיוצגת על ידי פאזור, משוואות דיפרנציאליות הופכות למשוואות אלגבריות. תוצאה זו נובעת מהעובדה שהאקספוננט המרוכב במקרה זה הוא פונקציה עצמית של אופרטור הנגזרת עבור הערך העצמי :
כלומר רק המשרעת המרוכבת משתנה על ידי הגזירה. לעומת זאת, גזירת הפונקציה המקורית משנה גם את המשרעת וגם את המופע:
לכן הנגזרת לפי זמן של סינוסואידה הופכת – בייצוג פאזורי – להכפלה בתדירות הזוויתית וביחידה המדומה. באופן דומה, אינטגרציה של פאזור לפי הזמן שקולה לחלוקה באותה תדירות מדומה.
לדוגמה, המשוואה הדיפרנציאלית הבאה מתארת את המתח על הקבל במעגל RC:
כאשר מקור המתח במעגל הוא סינוסואידי (כמו בזרם חילופין):
המשוואה הדיפרנציאלית הופכת בייצוג פאזורי:
כאשר
פתרון המשוואה עבור פאזור המתח על הקבל נותן:
על מנת למצוא את המתח עצמו הנופל על הקבל, ראשית יש לבטא את כל המספרים המרוכבים בצורה קוטבית:
כאשר
מכאן שהפתרון המתקבל הוא:
ניתוח מעגלים[עריכת קוד מקור | עריכה]
בעזרת פאזורים, השיטות לפתרון מעגלי זרם ישר (DC) יכולות לשמש גם לפתרון מעגלי זרם חילופין (AC):
כאשר נקרא עכבה חשמלית.
- במעגל AC קיים רכיב הספק חשמלי אקטיבי , שמציין את ההספק הממוצע הנצרך על ידי המעגל, ורכיב הספק ריאקטיבי , שמציין העברת הספק בין רכיבי המעגל. ניתן להגדיר את ההספק המרוכב . חוק ההספק במעגל AC המבוטא בפאזורים:
- (כאשר הוא הצמוד המרוכב של ).
- חוקי קירכהוף עובדים עם פאזורים מרוכבים.
מהנאמר לעיל ניתן ליישם את השיטות לניתוח רשת נגדים בעזרת פאזורים כדי לנתח מעגלי AC בעלי תדר יחיד הכוללים נגדים, קבלים וסלילים. מעגלים בעלי ריבוי תדרים ומעגלים עם צורות גל שונות ניתן לנתח על ידי פירוק כל צורות הגל לרכיבים בעלי צורות גל סינוסיות שלכל רכיב יש תדר, גודל ופאזה משלו, ואז ניתוח כל תדר בנפרד למציאת המתח והזרם. עם זאת שיטה זו לא עובדת להספק כי ההספק מבוסס על מכפלת המתח בזרם.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- מערכות חשמל:חשמל ומגנטיות פרק ב'. פאזורים והיגבים, מתוך אתר כותר, ספרי לימוד.





































