חוקי קירכהוף
חוקי קירכהוף למעגלים (או חוקי קירכהוף) הם צמד חוקים פיזיקליים העוסקים בזרמים ומתחים במעגלים חשמליים, בתנאי קיום שדה חשמלי משמר, בו הפוטנציאל החשמלי הסקלרי מוגדר.
החוקים תוארו לראשונה על ידי גוסטב קירכהוף בשנת 1845. חוקים אלו היו במקור חוקים ניסיוניים, אולם, שני החוקים נובעים מחוקי שימור מטען ואנרגיה וניתן לקבל אותם ממשוואות מקסוול אשר נוסחו 19 שנה מאוחר יותר ב־1864. לחוקים מקום חשוב בניתוח מעגלים חשמליים.
מקרים פרטיים של חוקים אלו הם חיבור בטור וחיבור במקביל.
חוק הזרמים[עריכת קוד מקור | עריכה]

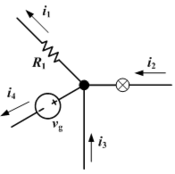
חוק הזרמים (Kirchhoff's Current Law או בקיצור KCL), נקרא גם החוק הראשון של קירכהוף או חוק הצומת.
החוק מסתמך על חוק שימור המטען – עבור כל נקודה במעגל שאין בה הצטברות של מטען, כל מטען שנכנס צריך גם לצאת. בהתאם לכך, סכום הזרמים הנכנסים לצומת חשמלי שווה לסכום הזרמים היוצאים ממנו. כלומר:
או – הסכום האלגברי של הזרמים הנכנסים לצומת ויוצאים ממנו שווה לאפס.
n מייצגת את כמות ה"ענפים" של הצומת שמהם הזרם נכנס או יוצא. לצורך החישוב, הזרמים הנכנסים לצומת מקבלים סימן חיובי והיוצאים סימן שלילי.
הוכחה לחוק הזרמים על ידי דיברגנץ[עריכת קוד מקור | עריכה]
ניתן להגיע לחוק הזרמים על ידי ביצוע פעולת הדיברגנץ על חוק אמפר המתוקן ושילוב עם חוק גאוס:
כלומר סכום הזרמים הנכנסים לנפח מסוים (כאשר אלה היוצאים הם שליליים) שווה לקצב השתנות צפיפות המטען שם. אם הצפיפות לא משתנה
() אזי סכום הזרמים הנכנסים שווה לאפס.
חוק המתחים[עריכת קוד מקור | עריכה]


חוק המתחים (Kirchhoff's voltage law או בקיצור KVL), נקרא גם החוק השני של קירכהוף.
החוק מסתמך על חוק שימור האנרגיה וטוען שסכום המתחים (הפרשי הפוטנציאלים) על פני לולאה סגורה כלשהי במעגל חייב להיות אפס (אחרת ניתן ליצור אנרגיה יש מאין). אם נקודת ההתחלה ונקודת הסיום הן אותה הנקודה לא יכול להיות הפרש פוטנציאליים בינה לבין עצמה. כלומר:
כאשר n מייצגת את מספר המתחים הנמדדים.
על פי חוק אוהם: כאשר:
- V מסמן מתח חשמלי בין שתי נקודות בגוף
- I מסמן זרם חשמלי בין שתי נקודות בגוף
- R מסמן את התנגדות הגוף העשוי מחומר אוהמי
הסימן של הזרם (חיובי או שלילי) נקבע בהתאם לכיוון הלולאה, כך שאם הזרם והלולאה באותו הכיוון הוא יהיה חיובי ואם הם בכיוונים מנוגדים הוא יהיה שלילי.
לאור זאת ניתן להגיע לניסוח נוסף לחוק המתחים: בכל לולאה סגורה במעגל, הסכום האלגברי של הכא"מים של כל המקורות שווה לסכום האלגברי של המכפלות IR.
המתח של כא"מ יחשב חיובי כאשר כיוון הלולאה הוא מההדק השלילי לחיובי.
גרסה נוספת לאותה המשוואה:
אם משתמשים בגרסה זו של המשוואה יש לזכור להפוך את כל הסימנים של IR.
הוכחה לחוק המתחים על ידי רוטור[עריכת קוד מקור | עריכה]
ניתן להגיע לחוק המתחים על ידי איפוס השינוי בשטף המגנטי בחוק פאראדיי:
משמע הרוטור של השדה שווה לאפס ולכן השדה הוא שדה משמר שאינו תלוי מסלול, ומכאן בלולאה סגורה הפרש הפוטנציאלים יהיה שווה לאפס.
ניתוח מעגל חשמלי באמצעות חוקי קירכהוף[עריכת קוד מקור | עריכה]
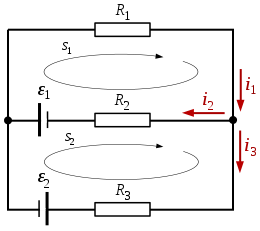
נתון מעגל חשמלי בעל שני מקורות מתח ושלושה נגדים.
בשלב הראשון מגדירים כיוון לזרמים במעגל. בשלב זה כיוון הזרמים עדיין לא ידוע, אם יש טעות הזרם הרלוונטי יצא שלילי.
על פי החוק הראשון:
בשלב השני מגדירים לולאות וקובעים עבור כל אחת מהן באופן שרירותי האם הכיוון החיובי יהיה נגד או עם כיוון השעון.
יישום החוק השני על לולאה s1 נותן:
יישום החוק השני על לולאה s2 נותן:
מכאן מתקבלת מערכת משוואות ליניאריות על ידי :
אם נתון
הפתרון הוא
ל- יש סימן שלילי, זה אומר שהכיוון של הוא הפוך מזה שהנחנו לצורכי הפתרון (כלומר, כיוונו הפוך לזה שנראה בציור).
מקרים פרטיים[עריכת קוד מקור | עריכה]
 ערך מורחב – חיבור בטור ובמקביל
ערך מורחב – חיבור בטור ובמקביל
בחיבור חשמלי בטור של שניים או יותר רכיבים חשמליים, הזרם שעובר בכל אחד מהרכיבים זהה, והמתח הכולל עליהם שווה לסכום המתחים על כל אחד מהם בנפרד.
בחיבור חשמלי במקביל של שניים או יותר רכיבים חשמליים, המתח על כל אחד מהם זהה, והזרם הכולל שעובר בהם שווה לסכום הזרמים שעובר בכל אחד מהם בנפרד.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- חוקי קירכהוף, באתר אנציקלופדיה בריטניקה (באנגלית)
| חשמל | ||
|---|---|---|
| מושגי יסוד | מטען • שדה חשמלי • אנרגיה פוטנציאלית חשמלית • פוטנציאל • מתח • כא"מ • זרם • התנגדות ומוליכות • עכבה • הספק • השראות • זרם ישר • זרם חילופין • מעגל חשמלי • תהודה • עכבה אופיינית | 
|
| רכיבים בסיסים | מקור מתח • מקור זרם • נגד • קבל • משרן • ממריסטור • שנאי • מפסק • מבדד | |
| מכשירי מדידה | מד מתח • מד זרם • מד התנגדות • אלקטרוסקופ • גלוונומטר • מד קיבול • מד השראות • רב מודד • אוסצילוסקופ • מחולל אותות | |
| אלקטרוניקה | מוליך למחצה • דיודה • טרנזיסטור • מיתוג • שפופרת ריק • טריודה • דיודה פולטת אור (לד) • מגבר שרת • מסנן תדרים • מעגל משולב • מעגל מודפס • VLSI • מיקרואלקטרוניקה | |
| זרם חזק | גנרטור חשמלי • מנוע חשמלי • תחנת כוח • מתקן חשמל דירתי • מערכת חלוקה • רשת חשמל • מערכת תלת-פאזית | |
| בטיחות בחשמל | התחשמלות • לוח חשמל • קצר חשמלי • נתיך • הארקה • ממסר פחת • מפסק אוטומטי • צבע חוטי החשמל | |
| חוקים פיזיקליים | חוק קולון • חוק גאוס • חוק אוהם • חוקי קירכהוף • חוק שימור המטען החשמלי • חוק פאראדיי | |