עצמות נפייר
עצמות נפייר הוא כינוי לעזר חישוב, שהומצא על ידי ג'ון נפייר על מנת להקל על חישוב פעולות כפל וחילוק, ומאפשר לבצען בעזרת פעולות חיבור וחיסור בלבד. כינוי נוסף לעזר חישוב זה הוא רבדולוגיה (ביוונית ραβδoς רבדוס הוא מוט והמשמעות של λóγoς היא מילה). במוטות מוטבעות או חרוטות עמודות מלוח הכפל, ובעזרתם מצטמצמת פעולות כפל לחיבור, ופעולות חילוק לחיסור. ניתן להיעזר בהם גם לחישוב שורש ריבועי. נפייר פרסם את המצאתו בעבודה שהודפסה באדינבורו שבסקוטלנד ב-1617.
נפייר נחשב לממציא הלוגריתם טבעי ולוגריתמים בכלל[1], שגם בעזרתם ניתן לבצע פעולות כפל וחילוק באמצעות חיבור וחיסור בלבד, שתי ההמצאות הללו קשורות בשמו, אך אינן קשורות זו לזו, ומבוססות על עקרונות מתמטיים שונים.
החשבונייה מורכבת מלוח התחום במסגרת. המשתמש מניח את מוטות נפייר בתוך המסגרת על מנת לבצע כפל או חילוק. הקצה השמאלי של הלוח מחולק ל-9 ריבועים הממוספרים מ-1 עד 9. מוטות נפייר מורכבים מרצועות עץ או מתכת, שעל אחת מפניהם או על שתיהן חרוטה שורה מלוח הכפל. עצמות נפייר הם מוטות בעלי חתך מרובע, שבכל אחת מארבע פניהם חרוטה עמודה כזו. אוסף של "עצמות" כאלו עשוי להיטמן באריזה נוחה לנשיאה.

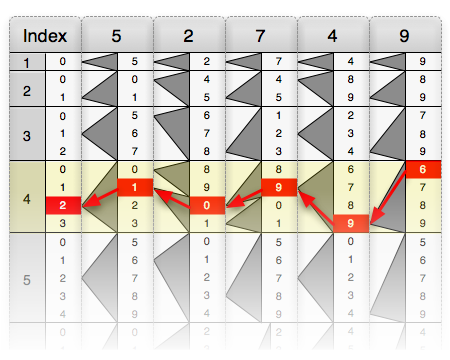
כל מוט מייצג ספרה מסוימת, ועל פניו מופיעה העמודה שמתאימה לעמודה של ספרה זו בלוח הכפל, בתשעה ריבועים, או משבצות, המייצגות את השורות בלוח. הריבועים, פרט לעליון, מחולקים לשניים על ידי קו אלכסוני, כשבמחצית אחת רשומה ספרת האחדות, ובמחצית השנייה ספרת העשרות של המכפלה המתאימה. להמחשה, בריבוע הרביעי של מוט 7, ובריבוע השביעי של מוט 4, המכפלה היא 28, ובשני ריבועים אלו מופיע 8 מתחת לאלכסון, ו-2 מעליו.
כפל[עריכת קוד מקור | עריכה]
לחישוב מכפלה, משתמשים במוטות המתאימים לספרות הנכפל, ומסדרים אותם במסגרת, כך שיופיע בשורה הראשונה. המשמעות היא שכדי לכפול מספר בן ארבע ספרות, נחוצים 40 מוטות, משום שאותה ספרה יכולה להופיע מספר פעמים בנכפל. כאשר המוטות חרותים משני צידיהם, די בעשרים מוטות לשם כך, ובדומה, די בעשר עצמות (שבכל אחת מהן ארבעה טורים) לכפל כול מספר בן ארבע ספרות. בעזרת עשרים עצמות אפשר לכפול במספר כלשהו בן 8 ספרות, ובעזרת שלושים, מספר בן 12 ספרות. בדוגמאות להלן הנכפל הוא בן שמונה ספרות או פחות, וניתן לבצען בעזרת ערכה של עשרים עצמות, או ארבעים מוטות החרותים משני צידיהם.
כאשר העצמות או המוטות המסודרים בקופסה רושמים מספר כלשהו, השורות בקופסה נותנות את המכפלה של מספר זה בספרה המתאימה לשורה. המכפלה לא רשומה ישירות בשורה, וכדי לקוראה, יש לחבר את ספרת האחדות, שרשומה בחלקו התחתון של הריבוע, עם ספרת העשרות של הספרה הקודמת, שרשומה בחלקו העליון של הריבוע במוט הקודם, ובמידת הצורך, להוסיף נשא מפעולת החיבור הקודמת. אחרי אימון קצר, המפעיל לומד "לקרוא" בקלות את המכפלה בספרה כלשהי מהשורה המתאימה בלוח. כדי לכפול במספר רב ספרתי, קוראים מהקופסה את המכפלה בכל אחת מספרות הכופל, ורושמים אותן זו מעל זו, לפי הסדר, ובהסטה המתאימה. כשכל המכפלות החלקיות רשומות, מחברים אותן לקבלת המכפלה.
חלקה השני של הפעולה זהה למעשה לחלק השני של שיטת הכפל שנלמדת בבתי ספר, כשההבדל הוא שהשיטה המקובלת דורשת לזכור את לוח הכפל - טבלה בת מאה תאים, אך עקב סימטריות הכפל והתנהגות 0 ו-1, המשמעות היא שיש לזכור 36 מכפלות "מעניינות".
- דוגמה
נחשב את מכפלת 46,785,399 ב-7. יש להניח על הלוח את המוטות שמתייחסים ל-46,785,399 כפי שניתן לראות באיור ולקרוא את התוצאה מהרצועה האופקית בשורה 7 שמספרה מופיע בצד הלוח. על מנת להפיק את המכפלה, יש לשים לב, עבור כל מקום מימין לשמאל, אילו מספרים נמצאו על ידי הוספת ספרות בחלקים האלכסוניים של הרצועה (תוך שימוש בנשא היכן שהסכום הוא 10 או יותר).

אם נתבונן באיור מימין לשמאל, ספרת האחדות היא (3) (האלכסון הראשון מכיל 3 בלבד), ספרת העשרות היא (6+3=9) (שכן האלכסון השני מכיל את הספרות 6 ו-3), ספרת המאות היא (6+1=7) וכך הלאה. יש לשים לב שבמיקום של ספרת המאות אלפים, היכן ש-5+9=14 אנו מותירים את הספרה 4 ואת הנשא 1 אנו מעבירים לחיבור הבא (נבצע דבר דומה עבור ספרת העשרה מיליון עבורה מתקיים 4+8=12).
כדי להכפיל את המספר 46,785,399 ב-96,431. כמו במקרה שהוצג לעיל נכפול את המספר 46,785,399 קודם ב-9 אחר כך ב-6, 4, 3 ו-1. לאחר מכן נמקם את המכפלות במקומות מתאימים ונסכם אותן ב"שיטת נייר ועפרון" רגילה.

בכפל שברים הכתובים בצורה עשרונית, הפעולות מתבצעות באופן זהה, ומיקום הנקודה העשרונית הוא סכום מיקומן בכופל ובנכפל: כשבנכפל שלוש ספרות אחרי הנקודה, ובכופל שתיים, במכפלה הנקודה תופיע לפני הספרה החמישית מימין, כלומר במכפלה תופענה חמש ספרות אחרי הנקודה.
חילוק[עריכת קוד מקור | עריכה]
חילוק יכול להתבצע באותו אופן. נחלק 46,785,399 ב־96,431. נניח את המוטות של המחלק (96431) על הלוח כפי שמומחש באיור שלהלן. באמצעות החשבונייה, נמצא את כל המכפלות של המחלק עם הספרות 1 עד 9 על ידי קריאת המספרים המוצגים. יש לשים לב שהמחולק בעל 8 ספרות בעוד שלמכפלות שהתקבלו על ידי כפל בספרות 1 עד 9 יש תמיד 6 ספרות (למעט המכפלה הראשונה בספרה 1). זו הסיבה שיש באופן זמני לקטום את הספרות "99" שב-46,785,399 כך שיוותר המספר 467853. כעת, יש למצוא את אחת מ־9 המכפלות הגדולה ביותר שהיא קטנה מהמחלק הקטום. במקרה זה, המכפלה היא 385,724. כפי שניתן להבחין באיור שלהלן: מאחר ש־385,724 מצוי בשורה 4 של החשבונייה, נסמן "4" כספרה השמאלית ביותר של המנה. בנוסף יש לרשום את המכפלה שנבחרה (385,724), בישור לשמאל, מתחת למחלק המקורי ואז לחסר את שני הגורמים. ההפרש המתקבל הוא 8,212,999. יש לחזור על הצעדים שלעיל: קטימת המספר ל-6 ספרות, בחירת מכפלה גדולה ביותר קטנה מהמספר הקטום, כתיבת ספרת השורה כספרה הבאה של המנה ולבסוף הפחתת המכפלה הנבחרת מההפרש שנמצא בצעד הראשון. מעקב אחר האיור יבהיר את הצעדים המתבקשים. יש לחזור על הצעדים עד אשר תוצאת ההפרש קטנה מהמחלק. המספר הנותר הוא השארית.

בדוגמה שלעיל התקבלה המנה 485 (שכן נעשה שימוש במכפלות של שורות 4,8,5) ושארית 16,364. ניתן לעצור כאן ולהשתמש בצורה השברית של התשובה .
מציאת שורש ריבועי[עריכת קוד מקור | עריכה]
מציאת השורש הריבועי עושה שימוש בעצם נוספת שנראית מעט שונה מהיתר שכן היא מכילה 3 עמודות. העמודה הראשונה בעלת 9 ריבועים 1, 4, 9, ... 64, 81, העמודה השנייה מכילה מספרים זוגיים 2 עד 18 והעמודה האחרונה מכילה מספרים מ 1 עד 9.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | √ | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0/1 | 0/2 | 0/3 | 0/4 | 0/5 | 0/6 | 0/7 | 0/8 | 0/9 | 0/1 2 1 |
| 2 | 0/2 | 0/4 | 0/6 | 0/8 | 1/0 | 1/2 | 1/4 | 1/6 | 1/8 | 0/4 4 2 |
| 3 | 0/3 | 0/6 | 0/9 | 1/2 | 1/5 | 1/8 | 2/1 | 2/4 | 2/7 | 0/9 6 3 |
| 4 | 0/4 | 0/8 | 1/2 | 1/6 | 2/0 | 2/4 | 2/8 | 3/2 | 3/6 | 1/6 8 4 |
| 5 | 0/5 | 1/0 | 1/5 | 2/0 | 2/5 | 3/0 | 3/5 | 4/0 | 4/5 | 2/5 10 5 |
| 6 | 0/6 | 1/2 | 1/8 | 2/4 | 3/0 | 3/6 | 4/2 | 4/8 | 5/4 | 3/6 12 6 |
| 7 | 0/7 | 1/4 | 2/1 | 2/8 | 3/5 | 4/2 | 4/9 | 5/6 | 6/3 | 4/9 14 7 |
| 8 | 0/8 | 1/6 | 2/4 | 3/2 | 4/0 | 4/8 | 5/6 | 6/4 | 7/2 | 6/4 16 8 |
| 9 | 0/9 | 1/8 | 2/7 | 3/6 | 4/5 | 5/4 | 6/3 | 7/2 | 8/1 | 8/1 18 9 |
נמצא כעת את השורש הריבועי של 46,785,399 בעזרת העצמות. ראשית, נקבץ את הספרות בזוגות החל מימין כך שנקבל: 99 53 78 46[2].
לאחר מכן יש לקחת את הזוג השמאלי ביותר 46. יש לבחור את הריבוע הגדול ביותר על עצם השורש הריבועי אשר עדיין קטן מ-46. זהו המספר 36 מהשורה השישית.
מאחר שהשורה השישית נבחרה, הספרה הראשונה בפתרון היא 6. קריאת העמודה השנייה מהשורה השישית על עצם השורש הריבועי גוררת הצבת 12 על הלוח. כעת יש להפחית את הערך 36 בעמודה הראשונה מ-46. לזה נצרף את הזוג הבא של הספרות שהוא המספר 78. כך תתקבל השארית 1,078. בסוף שלב זה, הלוח וחישובי הביניים יראו כך:
|
_____________
√46 78 53 99 = 6
36
--
10 78
|
כעת יש לקרוא את המספר בכל שורה (תוך התעלמות מהעמודות השנייה והשלישית בעצם השורש הריבועי). למשל, את השורה השישית יש לקרוא כך:
- 0/6 1/2 3/6 → 756
כעת יש למצוא את המספר הגדול ביותר הקטן מהשארית הנוכחית 1,078. ניתן להיווכח ש-1,024 מהשורה השמינית הוא הערך הגדול ביותר שעדיין קטן מ-1,078.
|
_____________
√46 78 53 99 = 68
36
--
10 78
10 24
-----
54
|
כמו קודם, יש לצרף 8 כדי לקבל את הספרה הבאה של השורש הריבועי, ולהחסיר את הערך 1,024 של השורה השמינית מהשארית הנוכחית 1,078 כדי לקבל 54. יש לקרוא את העמודה השנייה של השורה השמינית, 16, ולמקם מספר על הלוח על פי ההנחיות הבאות. המספר הנוכחי על הלוח הוא 12. יש להוסיף לו את הספרה הראשונה של 16 ולצרף את הספרה השנייה של 16 לתוצאה. לכן יש למקם על הלוח: 12 + 1 = 13 → צרף 6 → 136
הלוח וחישובי הביניים נראים כעת כך.
|
_____________
√46 78 53 99 = 68
36
--
10 78
10 24
-----
54 53
|
כעת שוב, יש למצוא שורה עם הערך הגדול ביותר שעדיין קטן מהשארית 5,453. הפעם, זוהי השורה השלישית המכילה את הערך 4,089.
|
_____________
√46 78 53 99 = 683
36
--
10 78
10 24
-----
54 53
40 89
-----
13 64
|
הספרה הבאה של השורש הריבועי היא 3. יש לחזור על אותם צעדים כמו קודם ולחסר 4,089 מהשארית הנוכחית 5,453 על מנת לקבל 1,364 כשארית הבאה. כאשר מסדרים מחדש את הלוח, יש לשים לב שהעמודה השנייה של השורש הריבועי היא 6, ספרה בודדת. לכן יש לצרף 6 למספר הנוכחי 136 שמצוי על גבי הלוח. 136 → צירוף 6 → 1,366 כך מתקבל המספר 1,366.
|
_____________
√46 78 53 99 = 683
36
--
10 78
10 24
-----
54 53
40 89
-----
13 64 99
|
יש לחזור על הפעולות פעם נוספת. הערך המקסימלי על הלוח כעת אשר קטן מהשארית הנוכחית של 136,499 הוא 123,021 מהשורה התשיעית.
הלכה למעשה, לרוב אין צורך למצוא את הערך של כל שורה על מנת למצוא תשובה. ניתן לנחש באיזו שורה תהיה התשובה על ידי הסתכלות במספר שנמצא על העצמות הראשונות בלוח והשוואתו עם הספרות הראשונות של התוצאה. אולם בדיאגרמות אלה, מוצגים הערכים של כל השורות למען הבהירות. כדבר שבשיגרה, נצרף 9 לתוצאה ונפחית 123,021 מהשארית הנוכחית.
|
_____________
√46 78 53 99 = 6839
36
--
10 78
10 24
-----
54 53
40 89
-----
13 64 99
12 30 21
--------
1 34 78
|
כעת השתמשנו בכל הספרות של המספר שלנו, אך עדיין קיימת שארית. המשמעות היא שקיבלנו את החלק השלם של השורש אך עדיין יש חלק שברי. יש להבחין בכך שאם באמת קיבלנו את החלק השלם של השורש, התוצא הנוכחית בריבוע (6,8392 = 46,771,921) חייבת להיות הריבוע הגדול ביותר שעדיין קטן מהמספר 46,785,399.
הרעיון הזה משמש לאחר מכן להבנה כיצד פועלת השיטה, אך לעת עתה נמשיך לייצר ספרות נוספות של השורש.
כעת נחבר שני אפסים לשארית כדי לקבל שארית חדשה של 1,347,800. העמודה השנייה בשורה התשיעית של עצם הריבוע מכילה את הערך 18 והמספר הנוכחי על הלוח הוא 1,366. לכן נחשב : 1,366 + 1 → 1,367 → הוסף 8 → 13,678 ונציב 13,678 על גבי הלוח. הלוח וחישובי הביניים כעת נראים כך :
|
_____________
√46 78 53 99 = 6839.
36
--
10 78
10 24
-----
54 53
40 89
-----
13 64 99
12 30 21
--------
1 34 78 00
|
השורה התשיעית מכילה 1,231,101 וזהו הערך הגבוה ביותר שעדיין קטן מהשארית ולכן הספרה הראשונה של החלק השברי של השורש היא 9.
|
_____________
√46 78 53 99 = 6839.9
36
--
10 78
10 24
-----
54 53
40 89
-----
13 64 99
12 30 21
--------
1 34 78 00
1 23 11 01
----------
11 66 99
|
יש לחסר את הערך של השורה התשיעית מהשארית ולרפד באפסים כדי לקבל שארית חדשה שערכה 11,669,900. העמודה השנייה בשורה התשיעית מכילה 18 עם הערך 13,678 על גבי הלוח לכן יש לחשב:
- 13,678 + 1 → 13,679 → הוסף 8 → 136,798
ולהציב 136,798 על גבי הלוח.
|
_____________
√46 78 53 99 = 6839.9
36
--
10 78
10 24
-----
54 53
40 89
-----
13 64 99
12 30 21
--------
1 34 78 00
1 23 11 01
----------
11 66 99 00
|
ניתן להמשיך בצעדים אלה על מנת למצוא מספר ספרות כרצוננו. יש לעצור כאשר הושג הדיוק הרצוי או לחלופין כאשר השארית היא אפס ואז המשמעות היא שהשגנו את השורש הריבועי המדויק. כדי למצוא שורש של מספר שאינו שלם, למשל 54,782.917. הכול זהה, למעט העובדה שיש להתחיל על ידי קיבוץ כל הספרות משמאל ומימין לנקודה העשרונית בזוגות. כלומר יש לקבץ את 54,782.917 כך: 7 91. 82 47 5, ואז יש למצוא את השורש הריבועי מתוך זוגות אלה.
שינויים[עריכת קוד מקור | עריכה]
במהלך המאה ה-19, עצמות נפייר עברו שינוי על מנת שיהיו קלים לקריאה. המוטות החלו להיבנות בזווית של 65° כך שהמשולשים שאותם היה צורך לחבר היו מיושרים אנכית. במקרה זה, בכל ריבוע במוט, ספרת האחדות ממוקמת מימין וספרת העשרות (או ספרת האפס) ממוקמת משמאל. המוטות נבנו כך שהקווים האנכיים והאופקיים היו גלויים יותר מקו המפגש של המוטות. כך שני הרכיבים של כל ספרה בתוצאה היו קריאים יותר. ניתן להיווכח באיור עד כמה ברור ש: 987654321 כפול 5 = 4938271605.
מוטות ז'נאי-לוקאס[עריכת קוד מקור | עריכה]

ב-1891 פיתח מהנדס רכבות צרפתי, אנרי ז'נאי (Henri Genaille), שכלול של עצמות נפייר, המבוסס על מאמר של אדואר לוקאס, ומכונה מוטות ז'נאי-לוקאס, או מוטות ז'נאי. בעזרת המוטות נחסך הצורך ב"פענוח" העצמות על ידי חיבור ספרת היחידות לעשרות והוספת הנשא. המוטות בנויים באופן שכל ספרה בהם מעבירה את הנשא הנכון, כלומר ספרת העשרות שלה, לספרה הבאה.
תיאור[עריכת קוד מקור | עריכה]
כמו עצמות נפייר, כל מוט מתאים לספרה מסוימת. המוט בנוי מכותרת, הספרה עצמה, ותחתה תשע משבצות, שמתאימות למכפלת הספרה בספרות 1 עד 9.
בצידה הימני של כל משבצת רשומות ספרות, אחת תחת השנייה, ובצידה השמאלי חץ או שני חיצים, המצביעים על אחת הספרות במוט הבא. החץ מייצג את ספרת העשרות של המשבצת, ומחליף את הספרה השמאלית בעצמות נפייר.
הספרה העליונה במשבצת היא ספרת האחדות של המכפלה המתאימה של המוט בשורה. הספרות הבאות הן הספרות העוקבות, תוצאת החיבור עם ספרת העשרות מהמוט הקודם.
למשל, במוט "2", בשורה 8, המכפלה היא 16. לכן הספרה העליונה במשבצת זו היא 6: ספרת האחדות של 16. הספרות הבאות מוסיפות את ספרת העשרות מהמוט הקודם - לכל היותר 7, משום שזה הנשא המרבי כשכופלים ב-8. לכן במשבצת זו 8 ספרות. העליונה היא 6, והבאות הן 7, 8, 9, 0, 1, 2, ו-3.
ספרת העשרות של 16 היא 1, ולכן החץ, או המשולש, מצביע על הספרה השנייה במוט הבא. בספרה החמישית במשבצת נרשם 0, ויש להעביר למוט הבא "עוד עשר". זה נעשה על ידי פיצול המשולשים: מול הספרה 0, והספרות הבאות, נפתח משולש חדש, שמצביע לספרה השלישית במקום לשנייה במוט הבא.
שימוש[עריכת קוד מקור | עריכה]
הצעד הראשון בשימוש במוטות הוא כמו בעצמות נפייר: מסדרים את המוטות בתיבה כך שהשורה העליונה תרשום את הנכפל.
כמו במוטות נפייר, וכמו בכפל לפי לוח הכפל, מוצאים את המכפלה בכל אחת מספרות הכופל, ורושמים את המכפלות אחת מעל השנייה בהסטה הנכונה, ומחברים. החילוק מתבצע באותו אופן, כשההבדל בין שתי המערכות הוא הפשטות במציאת המכפלה בכל ספרה רצויה.
מציאת המכפלה בספרה מסוימת היא כדלקמן: מסתכלים על המוט הימני בשורה זו. הספרה העליונה שרשומה במשבצת היא ספרת האחדות של המכפלה. המשולש מצביע לספרת העשרות של המכפלה, במוט הבא, שמצביע לספרת המאות במוט שאחריו, וכן הלאה. ממשיכים בהכוונת המשולשים עד לספרה העליונה, שרשומה במוט האינדקס, לקבלת המכפלה כולה.
דוגמה[עריכת קוד מקור | עריכה]
בדוגמה הנכפל הוא 52749, ובתחילת הפעולה סודרו את המוטות המתאימים בלוח, כך שהנכפל רשום בשורה העליונה. משמאל למוטות הספרות נמצא מוט האינדקס. ספרת הכופל המודגמת היא 4, ולמען הבהירות, הוסתרו השורות מתחת 5, ושורה 4 הודגשה.
ספרת האחדות של המכפלה היא הספרה העליונה במוט הימני - 6. ספרת העשרות של המכפלה היא 3, והמשולש "מעביר" אותה למוט הבא בהצבעה על הספרה הרביעית, לקבלת ספרת העשרות, 9. ממשיכים בהכוונת המשולשים עד למוט האינדקס, וקבלת המכפלה כולה - 210996.
רושמים את המכפלה, ממשיכים לחשב באותו אופן את המכפלות בשאר ספרות הכופל, ומסכמים.
חישוב בעזרת המוטות הוא קל ונוח יותר מעצמות נפייר, והשימוש בהם התפשט במהירות, אך היה קצר ימים: הם הומצאו בשלהי המאה ה-19, והתפשטות השימוש במכונות חישוב שמה קץ לשימוש בהם, יחד עם השימוש בעצמות נפייר.
חשבונייה העושה שימוש בכרטיסים[עריכת קוד מקור | עריכה]
בנוסף לחשבוניית ה"עצמות" שתוארה לעיל, נפייר גם בנה חשבוניית כרטיסים. חשבוניות אלו מקובצות בהתקן שמצוי במוזיאון הארכאולוגיה הלאומי של ספרד. ההתקן הוא קופסה מהודרת עשויה עץ משובץ בעצם. באזור העליון ההתקן מכיל חשבוניית "עצמות" ובחלק התחתון מצויה חשבוניית הכרטיסים. החשבונייה האחרונה מכילה 300 כרטיסים ב-30 מגירות. 100 כרטיסים מוטבעים במספרים. ה-200 הנותרים מאפשרים למשתמש לראות רק מספרים מסוימים. על ידי סידור הכרטיסים ניתן לבצע הכפלות אפילו למספרים באורך 100 ספרות עם מספרים בני 200 ספרות.
בנוסף, דלתות הקופסה מכילות את החזקות הראשונות של הספרות, המקדמים של מקדמי החזקות הראשונות של הבינום של ניוטון ואת הנתונים המספריים של הפאון הרגולרי.
לא ברור מי היה יוצר הקופסה ואם היא ממקור ספרדי או שהגיעה ממקום אחר. סביר שבמקור היא השתייכה לאקדמיה הספרדית למתמטיקה או שהייתה מתנה מהנסיך מוויילס. הדבר היחיד שוודאי הוא שהקופסה נשמרה בארמון. משם היא הועברה לספריה הלאומית של ספרד ומאוחר יותר למוזיאון הארכאולוגיה הלאומי שם היא שמורה עד היום.
בשנת 1876, הממשלה הספרדית שלחה את ההתקן לתערוכה של התקנים מדעיים, שנערכה בקנסינגטון, שם עוררה הקופסה תשומת לב רבה.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- יישום JAVA של עצמות נפייר עבור שיטות נומריות שונות
- סריקת PDF של "רבדולוגיה"
- אודות עצמות נפייר
- יישום JAVA מקוון הממחיש את פעולת ההתקן
- מידע אודות מוטות נפייר (הקישור אינו פעיל) קישור ארכיון
- Gyrobot, קבצים למדפסת תלת מימד לערכת עצמות נפייר Napier's Bones (Manual Calculator), באתר Thingiverse.com, 2021
- עצמות נפייר, באתר MathWorld (באנגלית)
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ בסיס הלוגריתם הטבעי, שבדרך כלל נקרא e, מכונה גם "קבוע נפייר", על שמו
- ^ מספר כמו 85,399 יקובץ כך: 99 53 8, ולכן חשוב להתחיל מימין