פונקציה על

בערך זה |
במתמטיקה, פונקציה מקבוצה לקבוצה היא על אם כל איבר בקבוצה מתקבל כערך של הפונקציה. באופן פורמלי, פונקציה היא על , אם לכל איבר בטווח () של הפונקציה מתאים לפחות איבר אחד בתחום () שלה. במילים אחרות: התמונה של שווה לטווח שלה. בסימון מתמטי: לכל קיים כך ש-. במקרה זה לעיתים מסמנים: כדי לציין ש- היא על.
קיומה של התכונה תלוי בטווח עליו מוגדרת הפונקציה: כך למשל, הפונקציה המתאימה לכל אדם את אמו היא על אם הטווח הוא קבוצת הנשים שיש להן ילדים, אבל לא על אם הטווח שלה מוגדר כקבוצת כל הנשים (כי יש נשים שאין להן ילדים). מסיבה זו, מקובל לציין שפונקציה היא על קבוצה מסוימת (שפירושו: אם קבוצה זו תילקח כטווח הפונקציה, יתקיימו הדרישות לפונקציה על).
דוגמאות ודוגמאות נגד[עריכת קוד מקור | עריכה]
- הפונקציה המתאימה לכל מצביע בבחירות 2006 את המפלגה שעבורה הצביע היא על קבוצת המפלגות שהתמודדו בבחירות אלה, כי לכל מפלגה הצביע לפחות אדם אחד (לא היו מפלגות שזכו לאפס קולות).
- תהי הפונקציה המוגדרת לפי הנוסחה לכל x ממשי. פונקציה זו היא "על", משום שלכל , .
- לעומת זאת, הפונקציה המוגדרת להיות אינה על, כיוון שבעבור , למשל, לא קיים מקור ממשי המקיים את המשוואה .
- תהי (פונקציה מקבוצת הממשיים לקבוצת הממשיים האי שליליים) המוגדרת באותה צורה, אזי היא על, כיוון שלכל ממשי אי שלילי קיים המקור .
-
דוגמה לפונקציה על – לכל האיברים יש מקור בתחום
-
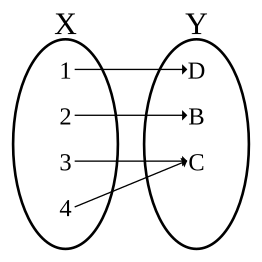
דוגמה לפונקציה שאינה על – לאיבר C שבטווח, אין מקור בתחום
תכונות[עריכת קוד מקור | עריכה]
עבור קבוצות סופיות, אם קיימת פונקציה מקבוצה לקבוצה שהיא על, אזי מספר האיברים ב- קטן או שווה למספר האיברים ב-. אם קיימת בין הקבוצות פונקציה שהיא חד-חד ערכית, אזי מספר האיברים ב- קטן או שווה למספר האיברים ב- ואם קיימת בין הקבוצות פונקציה שהיא חד-חד ערכית ועל, אזי מספר האיברים ב- שווה למספר האיברים ב-.
על הבסיס הזה בנה גאורג קנטור שיטה להשוות קבוצות אינסופיות, המהוות נושא מרכזי בתורת הקבוצות. קנטור הציג את המושג עוצמה כך ששתי קבוצות שיש ביניהן פונקציה שהיא חד-חד ערכית ועל הן שוות עוצמה.
משפטים מתורת הקבוצות[עריכת קוד מקור | עריכה]
- אם על, אז עוצמת גדולה או שווה לעוצמת (). משפט זה דורש שימוש באקסיומת הבחירה.
- אם על, אז על.
- אם ו- שתיהן על, אזי על גם היא.
אפימורפיזמים[עריכת קוד מקור | עריכה]
בתורת הקטגוריות, מורפיזם נקרא אפימורפיזם אם לכל אובייקט ולכל זוג מורפיזמים מתקיים שאם אז . בקטגוריה של קבוצות, המושגים פונקציה על ואפימורפיזם מתלכדים, אך יש קטגוריות, כגון הקטגוריה של חוגים, שבהן יש אפימורפיזמים שאינם פונקציות על.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- פונקציה על, באתר MathWorld (באנגלית)
- פונקציה על, באתר אנציקלופדיה בריטניקה (באנגלית)
- גדי אלכסנדרוביץ', תורת הקבוצות - פונקציות חד-חד-ערכיות, על והפיכות, באתר "לא מדויק", 15 במאי 2020