פעולה על סיביות
בתכנות מחשבים, פעולה על סיביוֹת (באנגלית: Bitwise operation) מופעלת על רצף סיביות אחד או יותר, כאשר הפעולה מופעלת על כל אחת מהסיביות בנפרד. זו פעולה מהירה ופרימיטיבית הנתמכת ישירות על ידי המעבד, ומשתמשים בה לצורך השוואות וחישובים.
במעבדים בעלות נמוכה, בדרך־כלל, פעולות על סיביות מהירות משמעותית מפעולות חילוק, מהירות מכפל, ולעיתים מהירות אפילו מפעולות חיבור. אף־על־פי שמעבדים כיום מבצעים חיבור וכפל במהירות הזהה לפעולות על סיביות בזכות השימוש בצינור הוראות ובחירות אחרות הקשורות בעיצוב ארכיטקטורת מעבדים, פעולות על סיביות בדרך־כלל משתמשות בפחות חשמל עקב השימוש בפחות משאבים.[1]
פעולות על סיביות[עריכת קוד מקור | עריכה]
 ערך מורחב – אלגברה בוליאנית
ערך מורחב – אלגברה בוליאנית
בהסבר הכתוב מטה, סדר הסיביות הוא כך שמיקום הסיבית בעלת הערך הנמוך ביותר נמצאת בצד ימין, וההתקדמות היא כלפי שמאל. לדוגמה, עבור הערך הבינארי 0001 (שערכו הדצימלי 1) יופיעו אפסים בכל מקום חוץ מאשר במיקום הראשון של המספר.
NOT[עריכת קוד מקור | עריכה]
הפעולה NOT על סיביות, או השלמה, היא פעולה אונארית שמבצעת שלילה לוגית עבור כל אחת מהסיביות, ומייצרת את המספר המשלים ל־1 עבור ערך בינארי נתון. סיביות שהיו 0 הופכות להיות 1, וסיביות שהיו 1 הופכות להיות 0. לדוגמה:
NOT 0111 (שערכו 7 בבסיס דצימלי) 1000 = (ערכו 8 בבסיס דצימלי)
תוצאתה של פעולת השלמה שכזו תמיד תהיה גדולה באחד מהייצוג של המספר שעליו בוצעה הפעולה בצורת המשלים ל־2. אם משתמשים בשיטת המשלים ל־2, אז:
- NOT x = -x - 1.
עבור מספרים שלמים אי־שליליים, פעולת המשלים על מספר מסוים תפעל כמעין "מראה" שתחזיר את המספר התואם לו בחצי השני של טווח המספרים האי־שלילי. לדוגמה, עבור מספרים אי־שליליים בני 8 סיביות יתקיים NOT x = 255 - x. ניתן להמחיש זאת על ידי גרף עם שני קטעים, אחד העולה מ־0 עד 255 והשני היורד מ־0 ועד 255. צורה פשוטה להמחיש רעיון זה תהיה להפוך את הצבעים של תמונה בגווני אפור (grayscale image) בה כל פיקסל מאוחסן כמספר שלם אי־שלילי.
AND[עריכת קוד מקור | עריכה]
הפעולה AND על סיביות לוקחת שני ייצוגים בינאריים של מספרים באורך זהה, ומבצעת פעולת וגם לוגית על כל זוג סיביות תואם על ידי הכפלה שלהם. זאת אומרת שאם שתי הסיביות הן 1, הסיבית שתצא היא 1 (שכן 1 × 1 = 1); אחרת, התוצאה היא 0 (שכן 1 × 0 = 0 וגם 0 × 0 = 0). לדוגמה:
0101 (שערכו 5 בבסיס דצימלי) AND 0011 (שערכו 3 בבסיס דצימלי) 0001 = (שערכו 1 בבסיס דצימלי)
ניתן להשתמש בפעולה כדי להחליט האם סיבית מסוימת דלוקה (1) או כבויה (0). לדוגמה, כדי להחליט האם הסיבית השנייה דלוקה בתוך רצף הסיביות 0011 (שערכו הדצימלי 3), ניתן להשתמש בפעולה AND על רצף סיביות שכולל 1 רק בסיבית השנייה:
0011 (שערכו 3 בבסיס דצימלי) AND 0010 (שערכו 2 בבסיס דצימלי) 0010 = (שערכו 2 בבסיס דצימלי)
מכיוון שהתוצאה 0010 אינה אפס, אנחנו יודעים שהסיבית השנייה ברצף הסיביות המקורי הייתה דלוקה. לטכניקה זו קוראים bit masking. (כאנלוגיה לשימוש של הדבקת נייר דבק, או מסיכות – masks, על החלקים שאין צורך לשנות או על אלו שאין בהם עניין. במקרה זה, עשינו masking על הסיביות שאין בהן עניין.)
ניתן להשתמש גם בפעולה AND על־מנת לכבות סיבית מסוימת ברצף הסיביות. לדוגמה, עבור הרצף 0110 (שערכו הדצימלי 6), אפשר לכבות את הסיבית השנייה על ידי ביצוע פעולת AND עם רצף הסיביות שבו יש אפס רק בסיבית השנייה:
0110 (שערכו 6 בבסיס דצימלי) AND 1101 (שערכו 13 בבסיס דצימלי) 0100 = (שערכו 4 בבסיס דצימלי)
בזכות תכונה זו, קל לבדוק את הזוגיות של מספר בינארי על ידי בדיקה של הסיבית התחתונה שלו. ניתן להשתמש ב־AND לכך כמו בדוגמה הבאה:
0110 (שערכו 6 בבסיס דצימלי) AND 0001 (שערכו 1 בבסיס דצימלי) 0000 = (שערכו 0 בבסיס דצימלי)
לכן 6 הוא מספר זוגי.
OR[עריכת קוד מקור | עריכה]
הפעולה OR על סיביות לוקחת שני ייצוגים בינאריים של מספרים באורך זהה, ומבצעת פעולת או לוגית על כל זוג סיביות תואם. התוצאה היא 0 אם שתי הסיביות הן 0, בעוד בכל מקרה אחר התוצאה היא 1. לדוגמה:
0101 (שערכו 5 בבסיס דצימלי) OR 0011 (שערכו 3 בבסיס דצימלי) 0111 = (שערכו 7 בבסיס דצימלי)
הפעולה OR יכולה לשמש כדי להדליק סיבית מסוימת ולהפוך אותה ל־1. כך, לדוגמה, ניתן להשתמש באוגר מסוים כדי לאחסן מספר, בו כל סיבית מייצגת מצב בוליאני נפרד. לפי דוגמה זו, רצף הסיביות 0010 (שערכו 2 בבסיס דצימלי) יכול לשמש כדי לאחסן מצבים של ארבעה דגלים שונים, כך שהדגלים הראשון, השלישי והרביעי מכובים, והדגל השני דלוק. ניתן לסמן את הדגל הרביעי כדלוק על ידי שימוש בפעולת OR בין ערך זה לבין רצף סיביות בו הסיבית הרביעית היא היחידה שדולקת:
0010 (שערכו 2 בבסיס דצימלי) OR 1000 (שערכו 8 בבסיס דצימלי) 1010 = (שערכו 10 בבסיס דצימלי)
טכניקה זו יעילה במיוחד לאחסון מספר ערכים בוליאניים למטרות חיסכון בזיכרון.
XOR[עריכת קוד מקור | עריכה]
הפעולה XOR על סיביות לוקחת שני ייצוגים בינאריים של מספרים באורך זהה, ומבצעת פעולת או מוציא לוגית על כל זוג סיביות תואם. התוצאה היא 1 אם רק הסיבית הראשונה היא 1 או אם רק הסיבית השנייה היא 1, אבל 0 אם שתי הסיביות הן 0 או ששתי הסיביות הן 1. בצורה זו אנחנו מבצעים השוואה בין שתי סיביות, כאשר התוצאה היא 1 אם שתי הסיביות שונות ו־0 אם שתי הסיביות זהות.
0101 (ערך 5 בבסיס דצימלי) XOR 0011 (ערך 3 בבסיס דצימלי) 0110 = (ערך 6 בבסיס דצימלי)
ניתן להשתמש בפעולת XOR כדי להפוך את מצבן של סיביות מסוימות. ניתן להפוך את המצב של סיבית מסוימת על ידי ביצוע פעולת XOR עליה עם 1. לדוגמה, בהינתן רצף הסיביות 0010 (שערכו 2 בבסיס דצימלי) ניתן להפוך את הסיבית השנייה והרביעית אם נעשה פעולת XOR עם רצף סיביות הכולל 1 במקום השני ובמקום הרביעי:
0010 (שערכו 2 בבסיס דצימלי) XOR 1010 (שערכו 10 בבסיס דצימלי) 1000 = (שערכו 8 בבסיס דצימלי)
ניתן להשתמש בטכניקה זו על מנת לשנות רצפי סיביות המייצגים רצפים של מצבים בוליאניים.
בשפת אסמבלי מתכנתים משתמשים לעיתים ב־XOR כקיצור על מנת לערוך את הערך של אוגר מסוים ל־0. תוצאת ביצוע הפעולה XOR על ערך מול עצמו תמיד תהיה אפס, ובארכיטקטורות מעבד רבות הפעולה לוקחת מספר קטן יותר של מחזורי שעון וזיכרון מאשר טעינת הערך אפס ושמירתו לתוך האוגר.
במתמטיקה[עריכת קוד מקור | עריכה]
בהנחה ש x > y, עבור כל מספר שלם אי־שלילי, ניתן להביע פעולות על סיביות באופן הבא:
כאשר הוא מספר הסיביות ב־ עבור כל .
הזזת סיביות[עריכת קוד מקור | עריכה]
הזזת סיביות נחשבת לעיתים כפעולה על סיביות, מכיוון שהיא מטפלת בערך כסדרה של סיביות ולא ככמות מספרית. בפעולה זו הסיביות זזות שמאלה או ימינה. לאוגרים במעבד המחשב יש גודל קבוע, ולכן סיביות "יזוזו החוצה" מהאוגר בצד אחד, בזמן שסיביות אחרות "יזוזו פנימה" מהצד השני. ההבדל בין סוגים שונים של הזזת סיביות טמון בערכים של הסיביות הנכנסות פנימה.
הזזה אריתמטית[עריכת קוד מקור | עריכה]

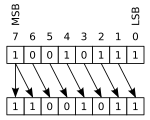
בהזזה אריתמטית, הסיביות שמוזזות החוצה לכל אחד מהצדדים אובדות. בהזזה אריתמטית לשמאל, אפסים זזים פנימה מצד ימין; ובהזזמה אריתמטית לימין, סיבית הסימן (הסיבית המשמעותית ביותר, MSB) זזה פנימה משמאל, וכך שומרת על הסימן של רצף המספר. המשפט האחרון אינו תקף לטיוטה האחרונה של תקן שפת C. אם בוצעה הזזה על ערך שלילי, התוצאה היא "תלוית מימוש", מה שאומר שאינה עקבית במעבר בין פלטפורמות.[2]
זו דוגמה להסטת מספר בן שמונה סיביות:
00010111 (שערכו +23 בבסיס דצימלי) הזזה-לשמאל = 00101110 (שערכו +46 בבסיס דצימלי)
10010111 (שערכו -105 בבסיס דצימלי) הזזה-לימין = 11001011 (שערכו -53 בבסיס דצימלי)
במקרה הראשון, הספרה השמאלית ביותר הוזזה מחוץ לאוגר, ו־0 חדש הוזז לתוך המיקום הימני ביותר. במקרה השני, הערך הימני ביותר 1 הוזז החוצה (ייתכן שלתוך דגל הנשא) ו־1 הועתק למיקום השמאלי ביותר על מנת לשמר את הסימן (אבל לא בהכרח, לפי הטיוטה האחרונה של שפת C. ראו הערה למעלה). הזזות מרובות יכולות להתבצע במכה. לדוגמה:
00010111 (שערכו +23 בבסיס דצימלי) הזזה-לשמאלה-שתי-פעמים = 01011100 (שערכו +92 בבסיס דצימלי)
הזזה אריתמטית לשמאל n פעמים זהה להכפלה ב־2n (בהינתן שלא הייתה גלישה נומרית), בזמן שהזזה אריתמטית לימין n פעמים בשיטת המשלים ל־2 זהה לחלוקה ב־2n ועיגול לעבר אינסוף שלילי. אם המספר הבינארי מטופל בצורת משלים ל־1, אז תוצאת הפעולת של הזזה ימינה היא חלוקה ב־2n ועיגול כלפי 0.
הזזה לוגית[עריכת קוד מקור | עריכה]
 |
 |
בהזזה לוגית, אפסים נכנסים במקום הסיביות שיצאו. מסיבה זו, הזזה אריתמטית והזזה לוגית לשמאל הן למעשה אותה פעולה בדיוק.
בניגוד להזזה לוגית לשמאל, בהזזה לוגית לימין סימן ה־0 נכנס לסיבית המשמעותית ביותר, במקום שתתבצע העתקה של סיבית הסימן. מסיבה זו, הזזה לוגית היא אידיאלית למספרים בינאריים אי־שליליים, בזמן שהזזה אריתמטית אידיאלית למספרים בינאריים בעלי סימן המיוצגים בשיטת המשלים ל-2.
סיבוב ללא סחיבה[עריכת קוד מקור | עריכה]
 |
 |
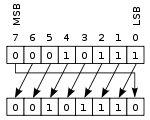
הזזה מעגלית (cyclic shift) הנקראת גם סיבוב סיביות (bitwise rotation), שימושית במספר תחומים ביניהם קומבינטוריקה, קריפטוגרפיה, תורת הקודים ועוד. והיא שימושית במיוחד כאשר רוצים לשמר את כל סיביות הערך.
הזזה מעגלית היא "סידור מחדש" של כל הכניסות ב-n-יה סדורה על ידי העתקה של כל כניסה פוזיציה אחת לשמאלה או לימינה ותכולת הכניסה האחרונה מועתקת לראשונה. בפעולה זו, הסיביות "מסתובבות" כאילו הקצה הימני והקצה השמאלי היו מחוברים במעין מעגל כמו שעון. למעשה הזזה מעגלית היא סוג של תמורה ציקלית שהיא עצמה מקרה פרטי של תמורה. בניסוח מתמטי אפשר להציג הזזה מעגלית כפונקציה על כניסות המחרוזת. למשל אם נתונה מחרוזת באורך סיביות, אם מתחילים מימין (כלומר הסיבית הכי פחות משמעותית נמצאת בפוזיציה 0):
הזזה מעגלית לשמאל היא:
- עבור כל הכניסות עד .
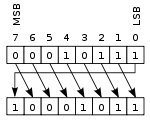
הזזה מעגלית לימין היא:
- עבור כל הכניסות עד .
חזרה על הזזה מעגלית פעמים תחזיר את מצב המחרוזת לקדמותו. במחשב ניתן לבצע הזזה מעגלית עם אופרטורי הזזה לימין ולשמאל המובנים בשפות התיכנות הנפוצות ומיוצגים בדרך כלל על ידי הסימנים ">>" ו-"<<" בהתאמה, כך:
- rotl(value, count) = (value << count) | (value >> (n - count))
- rotr(value, count) = (value >> count) | (value << (n - count))
סיבוב עם סחיבה[עריכת קוד מקור | עריכה]
 |
 |
סיבוב עם סחיבה דומה לסיבוב ללא סחיבה, אך שני הקצוות של האוגר מופרדים על ידי דגל הנשא. הסיבית שמוזזת פנימה (בצד כלשהו) היא הערך הישן של דגל הנשא, והסיבית שמוזזת החוצה (בצד השני) הופכת להיות הערך החדש של דגל הנשא.
סיבוב עם סחיבה פעם יחידה יכול לדמות הזזה לוגית או הזזה אריתמטית של מקום אחד על ידי הגדרת דגל הנשא לפני כן. לדוגמה, אם דגל הנשא מכיל 0, אז x סובב-לימין-עם-נשיאה-באחד הוא הזזה לוגית לימין, ואם דגל הנשא כולל עותק של סיבית הסימן, אז x סיבוב-לימין-עם-נשיאה-באחד הוא הזזה אריתמטית לימין. מסיבה זאת, בחלק מהמיקרו-בקרים כמו בקר PCI יש אפשרות לעשות רק סיבוב וסיבוב עם סחיבה, ואין אפשרות לעשות הזזה לוגית או אריתמטית.
סיבוב עם סחיבה שימושי במיוחד כאשר מבצעים הזזות על מספרים שגדולים יותר מגודל המילה הטבעי של המעבד, מכיוון שאם מספר גדול מאוחסן בשני אוגרים, הסיבית שמוזזת החוצה מאחד הצדדים של האוגר הראשון חייבת להיכנס בצד השני של האוגר השני. בעזרת סיבוב עם סחיבה, סיבית זו נשמרת בדגל הנשא במהלך ההזזה הראשונה, מה שמאפשר לה לזוז פנימה בהזזה השנייה בלי הכנה נוספת.
הזזה בשפות תכנות[עריכת קוד מקור | עריכה]
בשפות שנכתבו בהשראת C, פעולות ההזזה ימינה ושמאלה מיוצגות על ידי הסימנים "<<" ו־">>", בהתאמה. מספר המקומות שיש להזיז את הערך ניתן כאופרנד השני לפעולות ההזזה. לדוגמה:
x = y << 2;
עושה השמה לתוך x של התוצאה של הזזת y שתי סיביות לשמאל, שזהה להכפלתו ב־4.
תוצאת ההזזה יכולה להיות התנהגות תלוית הגדרה או כזו שאינה מוגדרת, כך שהשימוש בפעולה זו מתבצע בזהירות. התוצאה של הזזה מספר פעמים הגדול מגודל המילה בלתי מוגדרת ב־C וב־C++. הזזה לימין של ערך שלילי תלויה במימוש ונהוג שלא לעשותה;[3] התוצאה של הזזה לשמאל המתבצעת על מספר עם סימן גם היא לא מוגדרת במידה והתוצאה לא יכולה להיות מיוצגת כאותו טיפוס.[4] ב־C# הזזה לימין היא אריתמטית כשהאופרנד הראשון הוא int או long. אם האופרנד הראשון הוא uint או ulong, פעולת ההזזה ימינה היא הזזה לוגית.[5]
ראו גם[עריכת קוד מקור | עריכה]
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ "CMicrotek Low-power Design Blog". CMicrotek. נבדק ב-12 באוגוסט 2015.
{{cite web}}: (עזרה) - ^ Garcia, Blandine (2011). INTERNATIONAL STANDARD ISO/IEC 9899:201x (PDF) (201x ed.). ISO/IEC. p. 95. נבדק ב-7 בספטמבר 2015.
{{cite book}}: (עזרה) - ^ "INT13-C. Use bitwise operators only on unsigned operands". CERT: Secure Coding Standards. Software Engineering Institute, Carnegie Mellon University. נבדק ב-7 בספטמבר 2015.
{{cite web}}: (עזרה) - ^ JTC1/SC22/WG14 N843 "C programming language", section 6.5.7
- ^ "Operator (C# Reference)". Microsoft. נבדק ב-14 ביולי 2013.
{{cite web}}: (עזרה)

![{\displaystyle {\text{NOT }}x=\sum _{n=0}^{b}2^{n}\left[\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}+1\right){\bmod {2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d8b9a5eccb191c766402b2fc5380ebbc8426c80)

![{\displaystyle x{\text{ OR }}y=\sum _{n=0}^{b}2^{n}\left[\left[\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)+\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right)+\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right){\bmod {2}}\right]{\bmod {2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2fa2ae14fbfc48c9389875bec76a5a8c89d395e)
![{\displaystyle x{\text{ XOR }}y=\sum _{n=0}^{b}2^{n}\left[\left[\left(\left\lfloor {\frac {x}{2^{n}}}\right\rfloor {\bmod {2}}\right)+\left(\left\lfloor {\frac {y}{2^{n}}}\right\rfloor {\bmod {2}}\right)\right]{\bmod {2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a393e5bd48b7839dcfbfeef139b54dd98ea1f08b)







