במתמטיקה , טור מתכנס הוא הוא סכום של איברי סדרת מספרים .
בסדרה
{
a
1
,
a
2
,
a
3
,
…
}
{\displaystyle \left\{a_{1},\ a_{2},\ a_{3},\dots \right\}}
סכום החלקי ה-n-י -
S
n
{\displaystyle S_{n}}
S
n
=
∑
k
=
1
n
a
k
{\displaystyle S_{n}=\sum _{k=1}^{n}a_{k}}
טור הוא מוגדר כטור מתכנס אם סדרת הסכומים החלקיים שלו
{
S
1
,
S
2
,
S
3
,
…
}
{\displaystyle \left\{S_{1},\ S_{2},\ S_{3},\dots \right\}}
בשפה פורמלית, סדרה היא מתכנסת אם קיים גבול -
ℓ
{\displaystyle \ell }
ε
>
0
{\displaystyle \varepsilon >0}
שלם גדול
N
{\displaystyle N}
n
≥
N
{\displaystyle n\geq \ N}
|
S
n
−
ℓ
|
≤
ε
{\displaystyle \left|S_{n}-\ell \right\vert \leq \ \varepsilon }
כל טור שאינו מתכנס נקרא טור מתבדר .
טורים מתבדרים:
המספרים ההופכיים למספרים הטבעיים :
1
1
+
1
2
+
1
3
+
1
4
+
1
5
+
1
6
+
⋯
→
∞
.
{\displaystyle {1 \over 1}+{1 \over 2}+{1 \over 3}+{1 \over 4}+{1 \over 5}+{1 \over 6}+\cdots \rightarrow \infty .}
המספרים ההופכיים למספרים הראשוניים:
1
2
+
1
3
+
1
5
+
1
7
+
1
11
+
1
13
+
⋯
→
∞
.
{\displaystyle {1 \over 2}+{1 \over 3}+{1 \over 5}+{1 \over 7}+{1 \over 11}+{1 \over 13}+\cdots \rightarrow \infty .}
טורים מתכנסים:
חיבור וחיסור לסירוגין של המספרים ההופכיים למספרים הטבעיים:
1
1
−
1
2
+
1
3
−
1
4
+
1
5
⋯
=
ln
(
2
)
{\displaystyle {1 \over 1}-{1 \over 2}+{1 \over 3}-{1 \over 4}+{1 \over 5}\cdots =\ln(2)}
חיבור וחיסור לסירוגין של ההופכיים לאי-זוגיים (נוסחת לייבניץ לפאי):
1
1
−
1
3
+
1
5
−
1
7
+
1
9
−
1
11
+
⋯
=
π
4
.
{\displaystyle {1 \over 1}-{1 \over 3}+{1 \over 5}-{1 \over 7}+{1 \over 9}-{1 \over 11}+\cdots ={\pi \over 4}.}
המספרים ההופכיים למספרים המשולשיים :
1
1
+
1
3
+
1
6
+
1
10
+
1
15
+
1
21
+
⋯
=
2.
{\displaystyle {1 \over 1}+{1 \over 3}+{1 \over 6}+{1 \over 10}+{1 \over 15}+{1 \over 21}+\cdots =2.}
המספרים ההופכיים לעצרות :
1
1
+
1
1
+
1
2
+
1
6
+
1
24
+
1
120
+
⋯
=
e
.
{\displaystyle {\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{6}}+{\frac {1}{24}}+{\frac {1}{120}}+\cdots =e.}
ההופכיים למספרים הריבועיים (בעיית בזל ):
1
1
+
1
4
+
1
9
+
1
16
+
1
25
+
1
36
+
⋯
=
π
2
6
.
{\displaystyle {1 \over 1}+{1 \over 4}+{1 \over 9}+{1 \over 16}+{1 \over 25}+{1 \over 36}+\cdots ={\pi ^{2} \over 6}.}
ההופכיים לחזקות של 2:
1
1
+
1
2
+
1
4
+
1
8
+
1
16
+
1
32
+
⋯
=
2.
{\displaystyle {1 \over 1}+{1 \over 2}+{1 \over 4}+{1 \over 8}+{1 \over 16}+{1 \over 32}+\cdots =2.}
חיבור וחיסור באופן שווה (פעם חיסור, פעם חיבור) של ההופכיים לחזקות של 2:
1
1
−
1
2
+
1
4
−
1
8
+
1
16
−
1
32
+
⋯
=
2
3
.
{\displaystyle {1 \over 1}-{1 \over 2}+{1 \over 4}-{1 \over 8}+{1 \over 16}-{1 \over 32}+\cdots ={2 \over 3}.}
ההופכיים למספרי פיבונאצ'י :
1
1
+
1
1
+
1
2
+
1
3
+
1
5
+
1
8
+
⋯
=
ψ
.
{\displaystyle {\frac {1}{1}}+{\frac {1}{1}}+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{8}}+\cdots =\psi .}
מבחני התכנסות לטורים אם הטור הכחול,
Σ
b
n
{\displaystyle \Sigma b_{n}}
Σ
a
n
{\displaystyle \Sigma a_{n}}
יש מספר שיטות כדי לקבוע האם טור הוא טור מתכנס.
מבחן ההשוואה - האיברים של הסדרה
{
a
n
}
{\displaystyle \left\{a_{n}\right\}}
{
b
n
}
{\displaystyle \left\{b_{n}\right\}}
אם כל איבר בסדרה מקיים את הנוסחה
0
≤
a
n
≤
b
n
{\displaystyle 0\leq \ a_{n}\leq \ b_{n}}
∑
n
=
1
∞
b
n
{\displaystyle \sum _{n=1}^{\infty }b_{n}}
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
מבחן המנה . נניח שלכל איבר בסדרה,
a
n
>
0
{\displaystyle a_{n}>0}
r כך ש-
lim
n
→
∞
|
a
n
+
1
a
n
|
=
r
.
{\displaystyle \lim _{n\to \infty }\left|{\frac {a_{n+1}}{a_{n}}}\right|=r.}
אם 1>r , הסדרה מתכנסת. אם 1>r , הסדרה מתבדרת, אם 1=r , המבחן לא נותן מידע על התכנסות הסדרה.
מבחן השורש . נניח שאיברי הסדרה אי שליליים. נגדיר r כ:
r
=
lim sup
n
→
∞
a
n
n
{\displaystyle r=\limsup _{n\rightarrow \infty }{\sqrt[{n}]{a_{n}}}}
כאשר "lim sup" הוא החסם העליון . אם 1>r , הסדרה מתכנסת. אם 1>r , הסדרה מתבדרת, אם 1=r , המבחן לא נותן מידע על התכנסות הסדרה.
מבחן המנה ומבחן השורש מבוססים על השוואה לסדרה גיאומטרית, ולכן עובדים במקרים דומים. למעשה, אם מבחן המנה עובד, גם מבחן השורש עובד, אך לא להפך. לכן מבחן השורש חזק יותר ממבחן המנה, אבל הגבול קשה יותר לחישוב לרוב.
מבחן האינטגרל . הטור יכול להיות מושווה לאינטגרל . נניח ש-
f
(
n
)
=
a
n
{\displaystyle f(n)=a_{n}}
יורדת . אם
∫
1
∞
f
(
x
)
d
x
=
lim
t
→
∞
∫
1
t
f
(
x
)
d
x
<
∞
,
{\displaystyle \int _{1}^{\infty }f(x)\,dx=\lim _{t\to \infty }\int _{1}^{t}f(x)\,dx<\infty ,}
הטור מתכנס. אם האינטגרל מתבדר, גם הטור מתבדר.
מבחן ההשוואה הגבולית . אם
{
a
n
}
,
{
b
n
}
>
0
{\displaystyle \left\{a_{n}\right\},\left\{b_{n}\right\}>0}
lim
n
→
∞
a
n
b
n
{\displaystyle \lim _{n\to \infty }{\frac {a_{n}}{b_{n}}}}
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
אם ורק אם
∑
n
=
1
∞
b
n
{\displaystyle \sum _{n=1}^{\infty }b_{n}}
מבחן לייבניץ . המבחן אומר שלכל טור מהצורה
∑
n
=
1
∞
a
n
(
−
1
)
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}(-1)^{n}}
{
a
n
}
{\displaystyle \left\{a_{n}\right\}}
מבחן העיבוי של קושי . אם
{
a
n
}
{\displaystyle \left\{a_{n}\right\}}
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
∑
k
=
1
∞
2
k
a
2
k
{\displaystyle \sum _{k=1}^{\infty }2^{k}a_{2^{k}}}
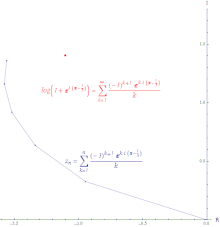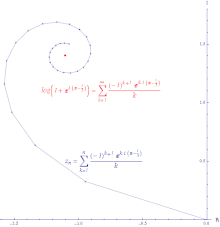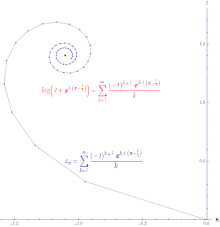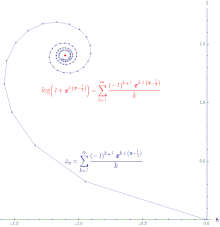
איור של התכנסות בתנאי שלטור החזקות של (log(z +1 מסביב ל-0 מוערכת ב- לכל סדרה
{
a
1
,
a
2
,
a
3
,
…
}
{\displaystyle \left\{a_{1},\ a_{2},\ a_{3},\dots \right\}}
a
n
≤
|
a
n
|
{\displaystyle a_{n}\leq \ \left|a_{n}\right\vert }
∑
n
=
1
∞
a
n
≤
∑
n
=
1
∞
|
a
n
|
.
{\displaystyle \sum _{n=1}^{\infty }a_{n}\leq \ \sum _{n=1}^{\infty }\left|a_{n}\right\vert .}
זה אומר שאם
∑
n
=
1
∞
|
a
n
|
{\displaystyle \sum _{n=1}^{\infty }\left|a_{n}\right\vert }
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
אם הטור
∑
n
=
1
∞
|
a
n
|
{\displaystyle \sum _{n=1}^{\infty }\left|a_{n}\right\vert }
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
אקספוננט מתכנס בהחלט בכל מקום.
אם הטור
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
∑
n
=
1
∞
|
a
n
|
{\displaystyle \sum _{n=1}^{\infty }\left|a_{n}\right\vert }
∑
n
=
1
∞
a
n
{\displaystyle \sum _{n=1}^{\infty }a_{n}}
משפט רימן אומר שאם טור מתכנס בתנאי אפשרי לסדר מחדש את האיברים של הטור כך שהטור יתכנס לכל סכום, או אפילו יתבדר.
[[קטגוריה:משפטים באנליזה]]
[[קטגוריה:תורת הטורים]]
 ערך מורחב – מבחני התכנסות לטורים
ערך מורחב – מבחני התכנסות לטורים





























![{\displaystyle r=\limsup _{n\rightarrow \infty }{\sqrt[{n}]{a_{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/787d1367e582bb131f4cdfb407def75a8655424c)








