חזקה (מתמטיקה)

בערך זה |
במתמטיקה, חֶזְקָה (או העלאה בחזקה) היא פעולה, המתבצעת בין שני מספרים: ה"בסיס" וה"מעריך". חזקה מסמנים בסימון כאשר a הוא הבסיס ו-b המעריך. בצורתה הבסיסית ביותר, שבה הבסיס הוא מספר ממשי והמעריך הוא מספר טבעי, חזקה מהווה קיצור של פעולת הכפל; כלומר - a בחזקת b היא המכפלה של b גורמים השווים כולם לבסיס: .
את הצורה הבסיסית הזו של חזקה ניתן להכליל למערכות מספרים רחבות יותר, ואף למבנים מתמטיים שבהם האיברים כלל אינם מספרים. על בסיס פעולת החזקה מגדירים פונקציות מתמטיות שמשמשות תדיר את כל תחומי המדעים.
טרמינולוגיה וסימון[עריכת קוד מקור | עריכה]

כאמור, את פעולת החזקה כאשר a הבסיס ו-b המעריך מסמנים ב-ab. סימון זה הוכנס לשימוש על ידי רנה דקארט ב-1637.[1] קדמו לו דרכים אחרות לרישום חזקה, החל מאוקלידס.[2] כאשר לא ניתן להשתמש בסימון המקובל, למשל במכונת כתיבה או בשפות תכנות מסוימות, נהוג הסימון a^b.[3] בשפות תכנות אחרות משמש הסימון a**b.[4]
הפעולה נקראת העלאה בחזקה (כגון "a בחזקת b" או "a מועלה בחזקת b"). כאשר המעריך הוא מספר טבעי בין 3 ל-10 (כולל) נהוג לקצר ולקרוא "a ב-n-ית", כאשר n הוא שם המספר הסודר. למשל "8 בשלישית", "2 ברביעית" ו"4 בעשירית" משמעם 83, 24 ו-410, בהתאמה. מקרה מיוחד הוא כאשר המעריך הוא 2, אז נהוג לקרוא לחזקה "a בריבוע", משום ששטח ריבוע שווה לאורך צלעו בחזקת 2. למשל "5 בריבוע" משמעו 52. התוצאה של העלאת מספר שלם בחזקה שנייה נקראת מספר ריבועי, או פשוט "ריבוע". תוצאת העלאת מספר שלם בחזקה שלישית נקראת לפעמים מספר מעוקב. המילה "חזקה" משמשת גם לציון תוצאת הפעולה.
מבחינת סדר פעולות חשבון, נהוג כי החזקה קודמת לארבע פעולות החשבון, וכי יש לחשב את המעריך לפני ביצוע פעולת החזקה:
- ,
- ,
- , וכדומה.
חזקה טבעית[עריכת קוד מקור | עריכה]
המופע הפשוט ביותר של חזקה הוא חזקה בעלת מעריך טבעי, כגון , כאשר המעריך מציין כמה פעמים יש לכפול את מספר הבסיס בעצמו. חזקה כזו אפשר להגדיר באמצעות נוסחת נסיגה: , ולכל מגדירים .
דוגמאות[עריכת קוד מקור | עריכה]
חוקי החזקות[עריכת קוד מקור | עריכה]
מהגדרה זו ניתן להסיק מספר מאפיינים בסיסיים של חזקות, הנקראים חוקי חזקות:[5]
| החוק | דוגמה |
|---|---|
דוגמאות לשימוש[עריכת קוד מקור | עריכה]
- האגדה מספרת שכאשר המלך הציע לממציא השחמט לקבוע את הגמול שיינתן לו תמורת המצאתו, אמר הממציא: "אדוני המלך, יינתן לי גרגר חיטה אחד במשבצת הראשונה של לוח השחמט, שני גרגרים במשבצת השנייה, ארבעה גרגרים במשבצת השלישית, וכך הלאה – בכל משבצת יינתן לי מספר גרגרים כפול מאשר בקודמתה". ציווה המלך על עבדיו לקיים את הבקשה, אך מהר מאוד גילה שבכל אסמי הממלכה אין מספיק חיטה. כמה גרגרים נדרש המלך לשים במשבצת האחרונה, היא המשבצת ה-64?
תשובה: ניתן לראות מתיאור משאלתו של הממציא, שבמשבצת ה- יש להניח גרגרים,[6] ולכן במשבצת ה- יש להניח גרגרים. במקום להשתמש במחשבון כדי לחשב מספר זה, ניתן להעריך את סדר הגודל של המספר אם נזכור כי , ניעזר בקירוב למספר זה: , שעמו קל יותר לחשב ידנית, ונשער את גודלו של המספר באמצעות חישוב על גב מעטפה.
בהתאם לחוקי החזקות, שהם יותר מאשר כפול , כלומר מספר בן 19 ספרות. התוצאה המדויקת היא 9,223,372,036,854,775,808. - אליס ובוב רוצים ליצור ביניהם ערוץ מאובטח להעברת מידע, כך שאיש מלבדם לא יוכל לקלוט את המידע העובר בו. לשם כך עליהם להחליט על מפתח סודי משותף שבעזרתו יוכלו להצפין ולקרוא את המידע שהם משתפים. אם אליס ובוב לא יכולים להיפגש, ההחלטה על המפתח הסודי חייבת להתקבל בערוץ קשר פומבי החשוף לכל. כדי להתגבר על בעיה זו פותח פרוטוקול דיפי-הלמן[7] שעושה שימוש בחוקי חזקות כדי לקבוע מפתח משותף סודי על גבי ערוץ פומבי. נוהל הפרוטוקול עובד כך:
אליס בוחרת מספר ובוב בוחר מספר . הם מחליטים יחדיו באופן פומבי וחשוף לכולם על קבועים ו- (שצריכים לעמוד בכמה דרישות טכניות). אליס מפרסמת את , שהוא השארית המתקבלת מחלוקת ב- (ראו חשבון מודולרי), ובוב מפרסם את . כעת אליס ובוב מנצלים חוק חזקה כדי להסכים על מפתח משותף. המפתח יהיה . בוב מסוגל לחשב את כי הוא יודע את ואת ולכן , ובאופן דומה אליס מסוגלת לחשב אותו כי . אף אחד אחר אינו מסוגל לגלות את , כי באופן פומבי פורסמו רק , וכאשר מספר גדול מאוד, קשה להסיק מתוכם את בלי לדעת את או את (ראו בעיית הלוגריתם הדיסקרטי).

חזקה שלמה[עריכת קוד מקור | עריכה]
הצעד הראשון בהכללת החזקה לקבוצה רחבה יותר של מספרים היא הרחבתה למעריכים שלמים (שאינם בהכרח חיוביים). הרחבה מוצלחת של החזקה צריכה להמשיך ולעמוד בחוקי החזקות התקפים לטבעיים. בפרט:
וכן:
לכן נוח להגדיר חזקת אפס כשווה ל-1 תמיד (ראו מכפלה ריקה) וחזקה שלילית בתור ההופכי לחזקה החיובית הנגדית. יוצא מן הכלל הוא הביטוי אפס בחזקת אפס שלרוב אינו מוגדר, או מוגדר כשווה ל-1.[8] בנוסף, חזקות שליליות של 0 אינן מוגדרות, כי לא ניתן לחלק באפס.
דוגמאות[עריכת קוד מקור | עריכה]
חזקה רציונלית[עריכת קוד מקור | עריכה]
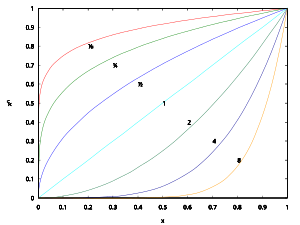
לכל n שלם (שונה מאפס), ולכל מספר ממשי חיובי a, קיים פתרון חיובי יחיד למשוואה . פתרון זה נקרא השורש ה-n-י של a, וסימונו .
בעזרת מושג השורש ניתן להרחיב את הגדרת החזקה גם למעריכים רציונליים כלשהם (ובסיס חיובי). תחילה מגדירים הרחבה למעריכים שהם שבר יסודי: יהי n מספר שלם ו-a מספר חיובי. נצפה כי יהיה מספר חיובי. כמו כן לפי חוקי חזקות מתקיים:
כלומר הוא השורש ה-n-י, ולכן:
.
בהתבסס על תוצאה זו ובעזרת חוקי חזקות נוכל להרחיב את ההגדרה לכל מעריך רציונלי (n שונה מאפס):
התוצאה אינה תלויה בבחירת ההצגה של השבר, משום ש-, ולכן הפעולה מוגדרת היטב. כל חוקי החזקות בשלמים נשמרים גם עבור מעריכים רציונליים.
במסגרת המספרים הממשיים, הוצאת שורש אינה מוגדרת היטב למספרים שליליים, ולכן גם חזקה רציונלית אינה מוגדרת לבסיס שלילי. אם הבסיס הוא 0, החזקה מוגדרת רק כשהמעריך חיובי, וערכה 0.
דוגמאות[עריכת קוד מקור | עריכה]
- אדם מפקיד בבנק 10 שקלים בריבית של 6% לשנה. כעבור שנה יהיו בחשבונו שקלים.
אם ישאיר סכום זה בחשבונו שנה נוספת, יצטבר בחשבון בסוף השנה השנייה סכום של שקלים.
בסוף השנה ה- יהיו בחשבונו שקלים.
עד כה המעריך היה שלם, אבל פיקדון בבנק ניתן למשוך במהלך השנה. מה יהיה הסכום שיצטבר לאחר שלוש שנים ושלושה חודשים (3.25 שנים)? הנוסחה הבסיסית לחישוב הריבית תקפה גם למעריך שאינו שלם, שהוא מספר רציונלי - בחשבון יצטבר סכום של שקלים.
חזקה ממשית[עריכת קוד מקור | עריכה]
ישנן שתי דרכים מקובלות ושקולות להגדרת חזקה עם מעריך ממשי.
דרך אחת היא להסתמך על החזקות הרציונליות שכבר הוגדרו. תכונה רצויה של פעולת החזקה היא שמירה על רציפות. מצופה שאם לכל חזקה נערוך סדרת חישובים מהצורה כש-x הולך ומתקרב ל-r, התוצאות שנקבל ילכו ויתקרבו לערך של . מסתבר כי דרישה זו מספיקה כדי להגדיר חזקה עם מעריך ממשי. מהבנייה של שדה המספרים הממשיים ידוע כי לכל מספר ממשי r קיימת סדרה של מספרים רציונליים המתכנסת ל-r. לכן לכל a אי-שלילי החזקה נתונה על ידי גבול הסדרה:
או באופן שקול כגבול של פונקציה:[9]
המעריכים בשני הגבולות רציונליים ולכן החזקה בהם מוגדרת היטב. גם הגדרה זו אינה תלויה בנציגים והתוצאה זהה לכל סדרה המכנסת ל-r. הגדרה זו גם מספקת דרך נומרית לחישוב על ידי קירובים הולכים ומשתפרים. לדוגמה ניתן לחשב את בכל רמת דיוק רצויה בזכות סדרת הקירובים:.
דרך שנייה היא בעזרת פונקציית האקספוננט . זוהי פונקציה בסיסית ביותר שניתן להגדירה בדרכים רבות ומגוונות, ללא הגדרה קודמת של חזקה ממשית. לדוגמה, (טור טיילור). מגדירים את הקבוע e בתור הערך (יש עוד דרכים רבות להגדיר את e). פונקציית האקספוננט מקיימת את הזהות:
בזכות זהות זו, שלמעשה היא צורת כתיב שונה של אחד מחוקי החזקות המוכרים, קל להוכיח כי פונקציית האקספוננט מתלכדת עם החזקות הרציונליות של e (למשל ). לכן ניתן להכליל את החזקות של e לכל מעריך ממשי על ידי ההגדרה:
פונקציית האקספוננט היא פונקציה רציפה ולכן הגדרה זו שקולה להגדרה הראשונה באמצעות גבול של סדרת חזקות רציונליות. כדי להרחיב את ההגדרה של חזקות של e להגדרה המתאימה לכל בסיס חיובי יש להגדיר את פונקציית הלוגריתם הטבעי . גם זו פונקציה בסיסית, שניתן להגדירה כפונקציה ההפוכה לאקספוננט (או בדרכים רבות נוספות, ואף לנקוט בגישה הפוכה: להגדיר קודם את הלוגריתם הטבעי ולאחריו את האקספוננט כפונקציה ההפוכה לו). כלומר אם , אז (הלוגריתם הטבעי מוגדר למספרים חיוביים בלבד). לפי הגדרה זו הלוגריתם הטבעי מקיים את הזהות . באמצעות זהות זאת וחוקי חזקות ניתן להגדיר לכל a חיובי חזקה ממשית:
ונותר רק המקרה בו הבסיס הוא 0 (שלא מוגדר לו לוגריתם טבעי). במקרה זה כל החזקות החיוביות שוות לאפס (והמקרה האי-חיובי אינו מוגדר).
דוגמאות[עריכת קוד מקור | עריכה]
חזקה מרוכבת[עריכת קוד מקור | עריכה]
- הערה: להבנת פרק זה דרושה היכרות עם מספרים מרוכבים.
שדה המספרים המרוכבים, שנבנה מתוך שדה המספרים הממשיים, יורש ממנו רבות מתכונותיו המועילות (כמו עצם היותו שדה) ומוסיף עליהן תכונות מועילות נוספות (כגון היותו סגור אלגברית). טבעי לנסות להכליל את ההגדרה המוצלחת של החזקה הממשית גם לחזקה מרוכבת. הכללה שכזאת ניתן לעשות בכמה כיוונים.
בסיס מרוכב ומעריך שלם[עריכת קוד מקור | עריכה]
כפל וחילוק מוגדרים היטב בין מספרים מרוכבים ולכן הכללת חזקה שלמה למספרים מרוכבים נעשית ללא קושי וללא שינוי בהגדרות.
דוגמאות[עריכת קוד מקור | עריכה]
- (שורש יחידה מסדר 3)
בסיס חיובי ומעריך מרוכב[עריכת קוד מקור | עריכה]
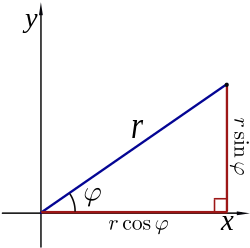
הגדרת העלאת מספר ממשי חיובי בחזקה ממשית התאפשרה לנו בזכות פונקציית האקספוננט. לפונקציית האקספוננט הכללה טבעית לכל מספר מרוכב. כיוון שזיהינו את האקספוננט הממשי עם הפונקציה , טבעי להמשיך במדיניות זו ולהגדיר חזקה מרוכבת של e בעזרת האקספוננט המרוכב. בצורה זו מתקבלת נוסחת אוילר: לכל x ממשי מתקיים,
כאשר מציין קוסינוס, מציין סינוס, ו- מציין את היחידה המדומה.
למען הנוחות נהוג גם להשתמש בקיצור . נוסחת אוילר עם הקיצור היא:
נוסחה זו מגדירה חזקה של e במספר מדומה. בעזרת חוקי החזקות ניתן להרחיב את ההגדרה לכל חזקה מרוכבת של e:
מנוסחה זו נובעת ההצגה הקוטבית של מספרים מרוכבים: אם z הוא מספר מרוכב שבמישור המרוכב מרחקו מאפס הוא r והזווית ברדיאנים בין הישר הממשי (ציר ה-x) לישר המחבר בין המספר לאפס היא θ (תטא), אז: . הצגה נוחה זו מאפשרת חישוב מכפלות וחזקות שלמות של מספרים מרוכבים (למשל באמצעות משפט דה-מואבר) ללא שימוש בבינום של ניוטון.
מכאן הדרך להגדרת חזקה מרוכבת של מספר ממשי חיובי a פשוטה, ונעשית בצורה דומה להגדרת החזקה הממשית:
כרצוי, הצבת חזקה ממשית בנוסחה (y=0) תתן את התוצאה הצפויה לחזקה ממשית.
באופן אנלוגי ניתן להגדיר חזקה של מספר ממשי כאשר המעריך הוא קווטרניון.
דוגמאות[עריכת קוד מקור | עריכה]
בסיס מרוכב ומעריך מרוכב[עריכת קוד מקור | עריכה]
מנקודת מבט שטחית נראה כי הנוסחה המגדירה חזקת מספר חיובי במספר מרוכב יאה לכל מקרה של מספר מרוכב בחזקת מספר מרוכב. אולם גישה זו נתקלת בבעיה מהותית. ההגדרה מסתמכת על קיומה של פונקציית הלוגריתם הטבעי ln גם במקרה המרוכב (שבמקרה המרוכב מסומנת log). אולם הגדרה אחידה ומוסכמת לפונקציה זו אינה קיימת. במקרה הממשי חיובי הפונקציה מוגדרת בקלות, כי לכל מספר חיובי y קיים x אחד ויחיד המקיים , ולכן ניתן להגדיר . כלומר הפונקציה היא חד-חד-ערכית ועל הממשיים החיוביים ולכן גם הפיכה. אך תכונה זו אינה נשמרת במספרים המרוכבים, וזאת משום המחזוריות של הפונקציות הטריגונומטריות הבסיסיות (להן יש מחזור של ). כתוצאה מכך האקספוננט המרוכב מחזורי בעצמו, עם מחזור של : לכל k שלם,
משמעות הדבר היא שלכל z מרוכב קיימים אינסוף מספרים מרוכבים x כך שמתקיים (למעט המקרה z=0, אז לא קיים אפילו x יחיד המקיים זאת); ההפרש בין כל שני ערכים כאלה הוא כפולה שלמה של . משום כך ניתן להגדיר את באינסוף דרכים שונות, כשלאף אחת מהן אין עדיפות. המסקנה היא שהלוגריתם הטבעי המרוכב הוא פונקציה רב-ערכית ושבכל הגדרה חד-ערכית של הלוגריתם הטבעי המרוכב יש ממד שרירותי שישפיע על תוצאותיה של החזקה המרוכבת. גרוע מזה, אם משנים בהדרגה את הערך של z לאורך מסילה המקיפה את הראשית במישור המרוכב כך שהשינוי ב-x רציף, אין חוזרים לאותו ערך. יש שתי גישות להתמודד עם קושי זה.
גישה אחת היא להתייחס לחזקה כפעולה שתוצאתה היא קבוצה של ערכים במקום ערך בודד. במקרה כזה התוצאה היא קבוצת כל הערכים שמתקבלים כתוצאת החזקה לכל בחירה אפשרית להגדרת הלוגריתם הטבעי המרוכב של המעריך. במקרה שהמעריך שלם, לכל אינסוף הערכים השונים של הלוגריתם של z כל תוצאות החזקה יתלכדו והתוצאה תהיה יחידה ושווה לערך המצופה מחזקה שלמה של מספר מרוכב. כאשר המעריך הוא מספר רציונלי (שבר מצומצם) אינסוף תוצאות יתלכדו ותתקבל קבוצה סופית של m ערכים, שהם הפתרונות למשוואה הפולינומית (z הבסיס, x הנעלם). כאשר המעריך אי-רציונלי הקבוצה תמנה אינסוף ערכים. החסרון הוא שבגישה זו תוצאת החזקה אינה מספר, אלא קבוצה (לעיתים אינסופית) של מספרים.
גישה שנייה היא לבחור "ענף", קטע בו הלוגריתם הטבעי המרוכב יהיה חד-ערכי. הענף הסטנדרטי הוא המגבלה (החלק המדומה של הלוגריתם מוגבל לתחום המצוין). במקרה הזה מתקבל למשל כי . לעומת זאת אם נבחר את הענף נקבל ולכן . החסרון בגישה הוא שבחירת הענף שרירותית והחזקה מפסיקה להיות רציפה (בקצות הענף).
דוגמאות[עריכת קוד מקור | עריכה]
- נחשב את :
- בגישת קבוצת הערכים: רציונלי ולכן קבוצת הערכים היא קבוצת פתרונות המשוואה , משוואה ריבועית שפתרונותיה הם ו-.
- בגישת הענף: נבחר את הענף הסטנדרטי. במקרה הזה ונקבל: .
- נחשב את :[10]
- בגישת קבוצת הערכים: לכל k שלם, (המקדם השלילי של k נועד לשם הנוחות, כיוון ש-k פרמטר שלם התוצאה לא תושפע). לכן ערכי הלוגריתם של i הם מהצורה: . לכן:
- , לכל k שלם.
- בגישת הענף: נבחר את הענף הסטנדרטי. במקרה הזה . כלומר k=0, ונקבל: .
- בגישת קבוצת הערכים: לכל k שלם, (המקדם השלילי של k נועד לשם הנוחות, כיוון ש-k פרמטר שלם התוצאה לא תושפע). לכן ערכי הלוגריתם של i הם מהצורה: . לכן:
מגדל חזקות[עריכת קוד מקור | עריכה]
ביטוי מהצורה (מעלים n מספרים אחד בחזקת השני) נקרא "מגדל חזקות"[11] (סדר החישוב הוא מהחזקה העליונה לתחתונה. כלומר, תחילה מחשבים את הביטוי , לאחר מכן, מחשבים את הביטוי , וכן הלאה). כאשר איברי מגדל חזקות זהים כולם, כלומר מספר a מועלה בחזקת עצמו n פעמים (מספר טבעי) קוראים לפעולה טטרציה (Tetration) ומסמנים אותה , או בסימון החץ של קנות' .[12] טטרציה היא חזקה מקוצרת כפי שחזקה היא כפל מקוצר. לדוגמה: .
כשם שניתן להגדיר סכום אינסופי ומכפלה אינסופית, ניתן להגדיר גם מגדל חזקות אינסופי. טטרציה אינסופית מוגדרת כגבול: , כאשר הגבול קיים. נסמן את הגבול ב-x. מתקיים: . כלומר הגבול (אם הוא קיים) הוא פתרון של המשוואה . אוילר הוכיח כי הגבול מתכנס בתחום (החסם העליון נובע מהשוויון שיצוין בהמשך).
דוגמאות[עריכת קוד מקור | עריכה]
- הוא פתרון של המשוואה , כלומר 2 או 4. במקרה הזה:
תכונות אלגבריות[עריכת קוד מקור | עריכה]
בניגוד לחיבור וכפל, המוגדרים לכל זוג ערכים, החזקה אינה מוגדרת אפילו בין כל שני מספרים ממשיים. מלבד זאת, לחזקה אין את רוב התכונות הבסיסיות השימושיות האופייניות לפעולות בינאריות מוכרות. לכן חזקה אינה הבסיס לאף מבנה אלגברי טיפוסי.
- חזקה אינה קיבוצית: לא תמיד . אפילו הדרישה החלשה יותר אינה מתקיימת (למשל ). מקובל כי כאשר לא מוסיפים סוגריים מבצעים קודם את החזקה העליונה: .
- חזקה אינה חילופית: בדרך כלל (למשל ).
- לחזקה אין איבר יחידה, אולם 1 הוא איבר יחידה ימני () ואין איבר יחידה שמאלי.
- כלל הצמצום הימני מתקיים לבסיסים אי-שליליים: אם a,b אי-שליליים, c שונה מ-0 ומתקיים אז (מעלים את שני האגפים בחזקת ההופכי של c). הכלל אינו מתקיים כשאין הגבלת סימן על הבסיס: .
- כלל הצמצום השמאלי מתקיים (במספרים ממשיים, כאשר החזקה מוגדרת) לכל בסיס שונה מ--1,0,1: אם אז .
- חזקה דיסטריבוטיבית משמאל מעל כפל לפי חוקי חזקות. היא אינה דיסטריבוטיבית מימין מעל כפל.
- תכונת הספיגה: 0 ו-1 סופגים ערכים משמאל: תמיד מתקיים ותמיד מתקיים (כאשר הביטוי מוגדר, ולמעט אפס בחזקת אפס).
הכללות[עריכת קוד מקור | עריכה]
חשבון אינפיניטסימלי[עריכת קוד מקור | עריכה]
חזקה בין סדרות וחזקה בין פונקציות ממשיות מוגדרת בקלות בעזרת החזקה בין מספרים ממשיים. לכל סדרה אי שלילית וסדרה ( חיובי כאשר ) קיימת סדרה . חזקה שומרת על התכנסות: אם אז מתקיים .
חזקה בין פונקציות ממשיות מוגדרת לכל x בו שתי הפונקציות מוגדרות והבסיס אי-שלילי (במקרה והבסיס הוא אפס, על המעריך להיות חיובי). חזקה בין פונקציות שומרת על רציפות של f ו-g בנקודה, אבל לא בהכרח שומרת על רציפות במידה שווה בקטע. לדוגמה ו- הן רציפות במידה שווה בכל הישר ואילו אינה כזו. אם פונקציית הבסיס ופונקציית המעריך גזירות, אז גם תוצאת החזקה גזירה ומתקיים (לפי כלל השרשרת וכלל לייבניץ):
תורת הקבוצות[עריכת קוד מקור | עריכה]
קבוצות ועוצמות[עריכת קוד מקור | עריכה]
בתורת הקבוצות הקבוצה מוגדרת כקבוצת כל הפונקציות מהקבוצה B אל הקבוצה A. בהתאם, אם ו- הן עוצמות, אז מגדירים: . תוצאת פעולת החזקה בין שתי עוצמות אינה תלויה בקבוצות הנציגות A ו-B שנבחרו לשם הצגת העוצמה. אם נבחן את הפעולה ביחס לעוצמות סופיות נקבל כי חזקה בין עוצמות מתלכדת עם חזקה בין מספרים טבעיים (כולל אפס). התלכדות זו מבטאת תוצאה קומבינטורית חשובה: לכל שני מספרים טבעיים n, m מספר הסדרות עם n איברים המורכבות ממספרים בין 1 ל-m (כולל הקצוות וחזרות מותרות) הוא (ובשפת הקבוצות: מספר הפונקציות מקבוצה מעוצמה n לקבוצה מעוצמה m הוא mn). למשל מספר הקודים בני שלוש ספרות המורכבים מהספרות 1–5 הוא 53=125. הגדרה זו מכסה גם את המקרה . לפיה תוצאת הפעולה שווה למספר הפונקציות מהקבוצה הריקה לעצמה. יש בדיוק פונקציה אחת כזאת (הפונקציה הריקה), ולכן התוצאה היא 1.
הגדרת החזקה בין עוצמות מאפשרת להתייחס גם לחזקות בין גדלים אינסופיים. לפי משפט קנטור לכל עוצמה מתקיים (הקבוצה , שהיא קבוצת כל הפונקציות המציינות של A, שקולה לקבוצת החזקה של A). זוהי תוצאה טריוויאלית לחזקות סופיות, אולם היא מבחינת חידוש מהפכני לחזקות אינסופיות, ומשמעותה שלכל עוצמה אינסופית יש עוצמה אינסופית גדולה ממנה. בפרט, ניתן להראות כי (2 בחזקת אָלֶף אֶפֶס שווה לעוצמת הרצף).
חוקי חזקות תקפים גם לחזקות של עוצמות, זאת מלבד החוקים המערבים חילוק, כיוון שפעולה זו אינה מוגדרת לעוצמות. כפל עוצמות מוגדר (הכפל באגף הימני הוא מכפלה קרטזית). כיוון שהקבוצה (הפונקציות מקבוצת המספרים מ-1 ל-n ל-A) שקולה לקבוצה (המכפלה הקרטזית של A עם עצמה n פעמים), מתקיים כי חזקת עוצמות היא כפל עוצמות מקוצר, בהתאם לתכונה המוכרת של חזקה. לכן מקובל הסימון לסימון המכפלה הקרטזית של A בעצמה n פעמים - היא קבוצת ה-n-יות הסדורות של איברי A (לדוגמה המרחב האוקלידי ה-n ממדי שמסומן מורכב ממכפלה של n עותקים של הישר הממשי ).
סודרים[עריכת קוד מקור | עריכה]
ניסיון להגדיר חזקה בין מספרים סודרים באופן אנלוגי לחזקה בין עוצמות נכשל בשל קיומם של סודרים רבים מאותה עוצמה. עם זאת, ניתן להגדיר חזקה בין סודרים על ידי הכללת החזקה בין מספרים טבעיים. ראשית מגדירים חיבור וכפל סודרים בדומה להגדרתם במערכת פאנו ובהתבסס על הסדר הטוב המוגדר בין הסודרים על ידי הכלה. חיבור בסודר עוקב מוגדר בדיוק כמו במספרים טבעיים ובנוסף מגדירים המטפל בסודר גבולי (סופרמום של קבוצת סודרים חסומה תמיד קיים כי בשל הסדר הטוב תמיד ישנו סודר מינימלי מבין כל החסמים). כפל מוגדר כשם שהוא מוגדר בטבעיים בתוספת (בניגוד לאינטואציה, חיבור וכפל סודרים אינם חילופיים). באופן דומה, חזקה בין סודרים מוגדרת באופן רקורסיבי על פי שלוש אקסיומות:
איזומורפי לקבוצת הפונקציות שיש להן תומך סופי, אשר מוגדר עליהן הסדר הלקסיקוגרפי כסדר טוב.
הכלל והכלל תקפים גם לחזקת סודרים, אך הכלל לא תמיד מתקיים.
אף על פי שחזקת עוצמות וחזקת סודרים מהווים שניהם הכללה לחזקת טבעיים (שניהם מתנהגים ככפל מקוצר כאשר המעריך טבעי), יש ביניהם שוני מהותי. למשל אף על פי שהסודר שווה לעוצמה , חזקת סודרים מקיימת בעוד שחזקת עוצמות מקיימת
אלגברה מופשטת[עריכת קוד מקור | עריכה]
אלגברה מופשטת עוסקת במבנים אלגבריים, שרובם מהווים הכללה או הפשטה של המספרים המוכרים עם פעולת הכפל. חזקה במעריך טבעי היא כתיב מקוצר לכפל, ולכן ניתן להגדירה גם בקבוצות אחרות בהן יש פעולה הדומה לכפל. לכל קבוצה עם פעולה בינארית מגדירים חזקה טבעית בדיוק כשם שהיא מוגדרת לכפל:
יש עניין בחזקה טבעית בעיקר כשהחזקות קיבוציות, כלומר, כל הדרכים להכפיל איבר x בעצמו n פעמים נותנות אותה תוצאה. תכונה זו מובטחת בכל חבורה למחצה, משום שהכפל קיבוצי, אבל היא אפשרית גם במקרים אחרים (ראו אלגברה עם חזקה אסוציאטיבית). במקרים כאלה מתקיימים מספר חוקי חזקות מוכרים:
כאשר לחבורה למחצה יש גם איבר יחידה (שנסמן ב-e) היא נקראת מונואיד וניתן להגדיר חזקת אפס בדומה להגדרה של 1 (איבר היחידה הכפלי) כתוצאה של חזקת אפס:
אם גם לכל איבר יש איבר הופכי (המסומן ) המבנה נקרא חבורה ואז ניתן להכליל גם לחזקות שלמות. כפי שבמספרים חזקה שלילית הוגדרה כהופכי של חזקה חיובית, כך נעשה בחבורה:
בפרט, הגדרה זו מצדיקה את הסימון לאיבר הופכי.
כאשר בנוסף לכל הפעולה של החבורה גם חילופית, החבורה נקראת חבורה אבלית ומתקיים הכלל המוכר:
בכל חבורה של מספרים עם כפל רגיל החזקה במובן המופשט שלה היא החזקה השלמה המוכרת. אולם החזקה המופשטת יכולה ללבוש צורות רבות נוספות. למשל בחבורה , שהיא קבוצת המספרים השלמים עם פעולת החיבור הרגילה ביניהם, החזקה המופשטת של החבורה היא פעולת הכפל המוכרת בין מספרים שלמים. זאת משום שכפל הוא חיבור מקוצר כשם שחזקה היא כפל מקוצר.
בתורת החבורות משמש לעיתים הסימון כאשר g ו-h איברים בחבורה כסימון לפעולת ההצמדה . יש דמיון מסוים בין הצמדה לבין חזקה, למשל מתקיימים הכללים:
אולם מעבר לכך אין לפעולות הרבה במשותף.
חישוב חזקות[עריכת קוד מקור | עריכה]
במקרים מסוימים יש צורך בחישוב חזקות עם מעריך טבעי גדול. דרך נאיבית לעשות זאת היא להכפיל בבסיס שוב ושוב. כלומר, אם המעריך הוא n, אז מבצעים n-1 פעולות כפל, בזמן ריצה שהוא מעריכי ביחס לאורך המעריך (מספר הספרות של n). שיטה זו אינה יעילה מספיק כאשר החישוב כולל מעריך בן עשרות או מאות ספרות, כפי שנדרש לעיתים באלגוריתמים קריפטוגרפיים.
באמצעות אלגוריתם פשוט ניתן לקצר את זמן החישוב משמעותית. כדי לחשב את נחשב את סדרת הערכים: (כל איבר הוא הריבוע של קודמו). נעצור כאשר נקבל את הערך הגדול ביותר בסדרה שאינו גדול מ- (כלומר האיבר האחרון הוא ). כל איבר התקבל מהאיבר הקודם בסדרה כפול עצמו, ולכן ביצענו (כאשר מסמן את פונקציית הרצפה) פעולות כפל בלבד כדי לחשב את הערכים בסדרה. לפי ההצגה של n בבסיס בינארי נכתוב את n כסכום של חזקות שונות של 2. כעת, לפי חוקי חזקות נוכל לחשב את כמכפלה של ערכים שונים בסדרה שבנינו. כיוון שבסדרה יש לכל היותר איברים, החישוב ידרוש פחות מ- פעולות כפל נוספות. בסך הכול, התהליך מתבצע בזמן ריצה פולינומי ביחס לאורך המעריך (כתלות בפעולת הכפל, שמתבצעת לכל היותר בזמן ריצה ריבועי). זהו קיצוץ משמעותי בזמן החישוב. כך למשל, אם n הוא מספר בן מאה ספרות עשרוניות, יידרשו כמה מאות פעולות כפל בלבד (במקום כגוגול פעולות בהכפלה חוזרת של הבסיס) לשם החישוב.
בתור דוגמה נחשב את . ראשית נחשב את איברי הסדרה:
| מספר המכפלות שחושבו | האיבר בסדרה |
|---|---|
| 0 | |
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 |
כעת נבחין כי ולכן:
- .
באופן זה חישבנו את בעזרת שבע פעולות כפל בלבד. חמש פעולות כדי לחשב את איברי הסדרה ושתי מכפלות נוספות כדי להגיע לתוצאה הסופית. על אף שמדובר במעריך קטן למדי, זה עדיין משמעותית פחות מ-36 פעולות כפל להן נדרשים בחישוב ישיר. אלגוריתמים סבוכים יותר מסוגלים לחשב אף במספר קטן יותר של פעולות, אך לא במידה משמעותית.
המהירות של שיטה זו תלויה במספר האחדות בייצוג הבינארי של המעריך. לכן כאשר בוחרים את המעריך ורוצים שהחזקה תהיה מהירה, בוחרים מספר עם מעט אחדות ביצוג הבינארי. למשל, באלגוריתם RSA נהוג לבחור e=65537 (שזה 10000000000000001 ביצוג בינארי)
שיטה זו פועלת לא רק למספרים, אלא לכל מקרה של חזקה מופשטת (עם חזקות קיבוציות). שימוש מעניין באלגוריתם הוא לחישוב מספרי פיבונאצ'י גדולים באמצעות חישוב חזקה של מטריצה (כקיצור של כפל מטריצות). הנוסחה הישירה לאיברי הסדרה מספקת את הזהות:
הפעלת האלגוריתם על המטריצה הפשוטה כבסיס, תחשב ביעילות כל שלשה של מספרי פיבונאצ'י סמוכים, גם כאשר האינדקס שלהם גדול מאוד.
פעולות הפוכות[עריכת קוד מקור | עריכה]
לא בכל הישר הממשי מתקיימים כללי הצמצום לגבי חזקה, ולכן אין לחזקה פעולה הפוכה מוגדרת היטב. בכל זאת, שימושי להגדיר לחזקה שתי פעולות שהפוכות לה תחת מגבלות מסוימות.
- שורש: שורש מסומן כאשר a אי-שלילי ו-b שונה מאפס, ותוצאת הפעולה היא המספר האי-שלילי היחיד x המקיים . מהגדרת החזקה הרציונלית נובע כי . פעולה זו מתאימה לתוצאת חזקה ומעריך כלשהו בסיס תואם (תחת תנאים המבטיחים כי קיים יחיד כזה).
- לוגריתם: לוגריתם מסומן כאשר b חיובי שונה מ-1 ו-a חיובי, ותוצאת הפעולה היא המספר הממשי היחיד x המקיים . פעולה זו מתאימה לתוצאת חזקה ובסיס כלשהו מעריך תואם (תחת תנאים המבטיחים כי קיים יחיד כזה).
הסיבה לכך שיש שתי פעולות הפוכות ולא אחת כמו בחיבור (חיסור) וכפל (חילוק) היא שחזקה אינה חילופית ואין סימטריה בין המעריך לבסיס (ככלל, לא ניתן להחליף ביניהם בלי לשנות את התוצאה). לכן נדרשות שתי פעולות נפרדות למציאת כל אחד.
פונקציות מבוססות חזקה[עריכת קוד מקור | עריכה]

פונקציות מבוססות חזקה הן פונקציות אלמנטריות בעלות מקום מרכזי באנליזה מתמטית.
- הפונקציה כאשר קבוע (ממשי או מרוכב). לפונקציה זו שני מקרים פרטיים חשובים:
- טבעי. אז הפונקציה נקראת מונום (חד-איבר). מצירופים ליניאריים של מונומים מתקבלים כל הפולינומים.
- כאשר n טבעי. אז הפונקציה נקראת השורש ה-n-י והיא מחזירה את השורש ה-n של x. הפונקציה מוגדרת למספרים אי-שליליים בלבד.
- הפונקציה כאשר קבוע אי-שלילי. פונקציה כזו נקראת פונקציה מעריכית.
מצירופים אריתמטיים והרכבת פונקציות ניתן לקבל מפונקציות אלו ואחרות עוד פונקציות רבות מבוססות חזקה. למשל .
עצרת מעריכית היא פעולה מבוססת חזקה שדומה לעצרת (המבוססת על כפל). שתי הפונקציות מוגדרות ברקורסיה זהה, רק שבמקרה של עצרת מעריכית חזקה מחליפה את הכפל.
משפטים ובעיות קשורות[עריכת קוד מקור | עריכה]
- חוקי חזקות נותנים מענה פשוט לחישוב החזקה של מכפלה: . נשאלת השאלה האם יש דרך אנלוגית לחישוב החזקה של סכום: . מענה לשאלה ניתן על ידי הבינום של ניוטון. אם a, b מספרים ממשיים ו-n מספר טבעי מתקיים:
- ( מסמן סכום ו- הוא מקדם בינומי)
- ניתן (באמצעות פיתוח טיילור) להכליל את נוסחת הבינום לכל r מרוכב:
- , כאשר
- לכל r לא טבעי זהו סכום אינסופי מתכנס. כאשר r טבעי, החל מהמקום ה-r+1 כל המקדמים מתאפסים ומתקבל הסכום הסופי המוכר.
- השערת קטלן, עוסקת בקיומם של מספרם עוקבים שהם חזקות.
- וריאציה של בעיית שטיינר שואלת מתי מתקיים השוויון (a ו-b חיוביים) מלבד המקרה הטריוויאלי בו a=b. אם נקח את השורש ה-ab של שני האגפים נקבל את השוויון השקול . מחקירת הפונקציה עולה כי הפונקציה מקבלת את הערך 1 בנקודה x=1, היא עולה לכל x קטן מ-e, כאשר x=e היא מקבלת מקסימום, היא יורדת לכל x גדול מ-e ושואפת ל-1 באינסוף. לכן לפי משפט ערך הביניים לכל a חיובי גדול מ-1 וקטן מ-e קיים בן זוג b גדול מ-e (ולהפך) כך ש-. לקבוע e עצמו אין בן זוג. המקרה היחיד בו בני הזוג שלמים הוא המקרה .
- הבעיה השביעית מתוך 23 הבעיות של הילברט שואלת האם לכל a אלגברי (ששונה מ-0 ו-1) ולכל b אלגברי אי-רציונלי מתקיים שהמספר טרנסצנדנטי. ב-1934 נתנה תשובה חיובית הנקראת משפט גלפונד-שניידר.
- בעיית וארינג שואלת האם לכל מספר טבעי k קיים מספר טבעי n כך שכל מספר טבעי ניתן להציג כסכום של לכל היותר n מספרים בחזקת k. הילברט הוכיח בשנת 1909 כי התשובה חיובית ובכך גרם להתפתחות מחקר ענף סביב מציאת n כתלות ב-k ופתרון שאלות נוספות בעלות אופי דומה. מקרה פרטי הוא משפט ארבעת הריבועים של לגראנז' הקובע כי כל מספר טבעי ניתן להציג כסכום של לכל היותר ארבעה ריבועים. התשובה לשאלה אילו מספרים ניתן להציג כסכום של שני ריבועים ידועה גם היא במדויק.
- קיימים אינסוף מספרים טבעיים a, b ו-c כך שמתקיים , אלו נקראים שלשות פיתגוריות. המשפט האחרון של פרמה קובע כי תופעה זו ייחודית, וכי לכל לא קיימת שלשה של מספרים טבעיים a, b ו-c כך שמתקיים . את המשפט הוכיח אנדרו ויילס בשנת 1995, למעלה מ-350 שנה לאחר שפרמה טען לנכונות המשפט ללא הוכחה. אוילר שיער השערה בעלת אופי דומה: לכל לא קיימת קבוצה של n מספרים כך שסכום החזקות ה-n-יות של כל המספרים מלבד האחרון שבהם, שווה לחזקה ה-n-ית של האחרון. ההשערה התבררה כשגויה כפי שניתן לראות מהדוגמה הנגדית: .
- שורש יחידה מסדר n (מספר טבעי) הוא מספר מרוכב z (או באופן כללי יותר, איבר שדה) כך שמתקיים . מבין המספרים הממשיים 1 ו--1 הם שורשי היחידה היחידים. אולם מבין המספרים המרוכבים ישנם n שורשי יחידה מסדר n. לשורשי היחידה תכונה מיוחדת שהחזקות השלמות שלהם מחזוריות באורך n. כלומר לכל k שלם (נובע מחוקי חזקות). למשל ל--1 מחזור באורך 2 ( שווה 1 כאשר k זוגי ו--1 כאשר k אי זוגי) המנוצל רבות להצגת סימנים מתחלפים (כמו בטורי לייבניץ). דוגמה אחרת היא שורש היחידה שלו מחזור באורך 4:
- על בסיס עובדה זו (ופיתוח טור מקלורן של האקספוננט והפונקציות הטריגונומטריות) מוכיחים את נוסחת אוילר שבעזרתה מגדירים חזקה מרוכבת.
- אחת הבעיות העתיקות במתמטיקה היא מציאת פונקציות פשוטות המחזירות אך ורק מספרים ראשוניים. ב-1947 הוכיח ויליאם מילס כי קיים קבוע A כך שלכל n טבעי הוא ראשוני (כאשר היא פונקציית הערך השלם).
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- Laws of Exponents חוקי חזקה עם דוגמאות (באנגלית)
 חזקות (אלגברה), דף שער בספרייה הלאומית
חזקות (אלגברה), דף שער בספרייה הלאומית
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ בספרו La Géométrie, Leyde, 1637, עמוד 299: ”et aa ou pour multiplier a par soi-même; et pour le multiplier encore une fois par a, et ainsi à l’infini”. להרחבה ראו "Earliest Uses of Symbols of Operation" (באנגלית)
- ^ John J. O'Connor and Edmund F. Robertson, Etymology of some common mathematical terms, MacTutor History of Mathematics archive
- ^ בשפת Visual Basic, למשל: ^ Operator
- ^ בשפת PL/I, למשל: PL/I Language Reference, עמ' 34
- ^ Exponent Laws, באתר MathWorld (באנגלית)
- ^ לו היו מונחים במשבצת הראשונה 2 גרגירים, היינו צריכים במשבצת ה- להניח גרגירים, אך כיוון שמונח בה גרגיר אחד, ביצוע פעולת החזקה מתחיל מהמשבצת השנייה, ועל כן יש להניח גרגרים במשבצת ה-.
- ^ Whitfield Diffie and Martin E. Hellman, New Directions in Cryptography, IEEE transactions on Information Theory 22(6), 1976, pp. 644-654
- ^ sci.math FAQ: What is 0^0?
"Wolfram Alpha calculates 0^0". Wolfram Alpha LLC. - ^ Denlinger, Charles G., Elements of Real Analysis, Jones and Bartlett, 2011, pp. 278–283
- ^ דוגמה לחישוב באתר Cut The Knot (באנגלית)
- ^ Power Tower, באתר MathWorld (באנגלית)
- ^ Donald E. Knuth, "Coping With Finiteness", Science 194(4271), December 1976, pp. 1235–1242.


















































![{\displaystyle \ {\sqrt[{n}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46683380a0177fb9a3f0e7e807ebb8a6a7b41c80)


![{\displaystyle \ a^{\frac {1}{n}}={\sqrt[{n}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d581d865bb13c16803b77067d45e970564622b4)
![{\displaystyle \ a^{\frac {m}{n}}={\left(a^{\frac {1}{n}}\right)}^{m}={\sqrt[{n}]{a}}^{m}={\sqrt[{n}]{a^{m}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7facd8c87147e2d66bf3abceb3d9a1e4f6039183)
![{\displaystyle \ {\sqrt[{km}]{a^{kn}}}={\sqrt[{m}]{a^{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a8c96983d926ac59d1b24b54c0a8590017b04d1)
![{\displaystyle \ 4^{\frac {1}{2}}={\sqrt[{2}]{4}}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3eb9b01bed266831cbb7fdeeef54d3501feed0cc)
![{\displaystyle \ 8^{\frac {2}{3}}={\sqrt[{3}]{8}}^{2}=2^{2}=4}](https://wikimedia.org/api/rest_v1/media/math/render/svg/711647f65cac840759b45cc4cbe4e735bbd13765)









































































![{\displaystyle \ {\sqrt[{x}]{x}}=a}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de1ef68bebb399ff0862c111a4ebfa14c0de00a9)
![{\displaystyle \ {\frac {1}{e^{e}}}\leq a\leq {\sqrt[{e}]{e}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/197466e74e4df3644ea72452722031bcdee28138)
![{\displaystyle \ \max[{\sqrt[{x}]{x}}]={\sqrt[{e}]{e}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d79e48fad570b67bd1148de85316e5056986e719)


![{\displaystyle \ {\sqrt[{x}]{x}}={\sqrt {2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e505bce756b9cd9185309218b95ea03b013e5b1b)




















































































![{\displaystyle \ {\sqrt[{b}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/955156ec98708049b1f6b1c9fa6b769a42adbe01)

![{\displaystyle \ {\sqrt[{b}]{a}}=a^{\frac {1}{b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbdb637c19b9c3a57572d04892ae0f46346709e0)






![{\displaystyle \ x^{\frac {1}{n}}={\sqrt[{n}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43b4e7fe42477a8eb595cef7cec32003e31439d1)









![{\displaystyle \ {\sqrt[{a}]{a}}={\sqrt[{b}]{b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fefd0b3a63cb5e3e3adf6f2f8655d37ba890bf4f)
![{\displaystyle \ {\sqrt[{x}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/773323ddc639733ec52dbce86617221212d6422a)














