משתמש:YossiAbramovAFM/הישברות חוט זורם

הישברות חוט זורם הוא תהליך המאופיין באי יציבות עקב הפרעה, שהיא לא בהכרח קטנה, המובילה להיצרות החוט באזורים שונים עד לשבירה מלאה והיפרדות חוט הזורם שהיה בתחילה רציף ליחידות זורם נפרדות.

מבחינה אנרגטית ניתן להסביר את התופעה על ידי קיום אנרגיה משטחית המאופיינת על ידי מכפלת מתח הפנים ושטח הפנים בין שני הזורמים. בהתאם לחוק השני של התרמודינמיקה מערכת פיזיקלית אשר עוברת ממצב שיווי משקל אחד לשני בתהליך ללא שינוי אנטרופיה כאשר רכיבי המערכת לא משנים את נפחם תשאף למזער את האנרגיה שלה , כאשר מקור האנרגיה היחיד הינו האנרגיה המשטחית ומתח הפנים קבוע המערכת תשאף למזער את שטח הפנים בין שני הזורמים וכתוצאה מכך לשבירת חוט הזורם ליחידות זורם נפרדות.

כאשר מדובר בנפילה חופשית של זורם ברדיוס אחיד הנשבר לטיפות אחידות במרווחים קבועים התופעה נקראת אי יציבות פלטו ריילי.

חוטים העשויים מזורם ואו יחידות המסה שניתן לייצר בעזרת הישברות חוט זורם רלוונטים באפליקציות רבות בהן מעבדה על שבב , תהליכי ציפוי והדפסה.

אי יציבות זו מופיעה בתהליכים שונים בטבע בהם יצירת קורי עכביש וטבעות אוויר אותם מייצרים דולפינים ולוויתנים.

היסטוריה

בחינת תהליך יצירת טיפות מתועד לראשונה בעבודתו של לאונרדו דה וינצ'י אשר כתב:

"איך לחלקיקי המים יש אחיזה עצמית. [...] זה נראה שבתהליך בו טיפה מתנתקת מחוט הנוזל, חוט הנוזל נמתח ככל שהוא יכול ע"י המשקל של הטיפה ואחרי שהטיפה מתנתקת מחוט הנוזל , חוט הנוזל נע מעלה בתנועה המנוגדת לטבע של דברים כבדים."

לכן לאונרדו דה וינצ'י ייחס את הסיבה לכך שהטיפה נופלת לכוח הכבידה ואת המנגנון המוביל לתנועה מעלה של חוט הנוזל לקוהזיה של מולקולות המים.

המנגנון הפיזיקלי לתהליך שבירת חוט הזורם מתואר על ידי משוואת יאנג-לפלס שהוסברה לראשונה באופן איכותי על ידי תומאס יאנג בשנת 1804 ובאופן מתמטי בשנת 1805 על ידי פייר-סימון לפלס. לפי משוואת יאנג-לפלס אם נסתכל על חלק המשטח המחבר בין חוט הזורם לבין הזורם מעליו נקבל כי כאשר העקמומיות הממוצעת בחוט קעורה הלחץ הפנימי בחוט גדל וכאשר העקמומיות הממוצעת בחוט קמורה הלחץ הפנימי קטן. בשנת 1833 פליקס סבר ביצע ניסויים בעזרת סילוני נוזל ותוך שימוש בשיטה הסטרובוסקופית גילה כי תהליך השבירה של חוט נוזל הינו תהליך ספונטני. בשנת 1873 במסגרת סיכום עבודת המחקר שלו ז'וזף פלטו הראה בעזרת ניסויים וכמו כן על ידי הוכחות מתמטיות שונות כי חוט הזורם נשבר עבור כל הפרעה אינפיטיסימאלית עם אורך גל הגדול מ-$2\pi r_{0}$ כאשר $r_{0}$ הוא רדיוס החוט ולאחר מכן בשנת 1879 ו-1892 הרחיב ג'ון ריילי עבודה זו למקרים דינמיים תוך שימוש באנליזת יציבות לינארית ומצא את התדר הלא יציב הגדול ביותר עבור 2 מקרים ספציפיים: חוט נוזל ניוטוני בעל צפיפות קבועה וצמיגות זניחה אשר מסביבו ואקום וחוט נוזל ניוטוני בעל צמיגות קבועה וצפיפות זניחה אשר מסביבו ואקום.

כאשר ההפרעות במערכת הופכות לגדולות לא היה ניתן להשתמש בתיאוריה אותה פיתח ריילי ובהיעדר כלים תיאורטים נדרשו ניסויים. בשנת 1887 פיליפ לנארד חקר את האוסילציות הנשארות בטיפות לאחר ההתנתקות כאשר ישנן הפרעות גדולות והראה שניתן לאמוד את מתח הפנים בעזרת מדידת התדר. במהלך ניסוי זה הוא תיעד באמצעות צילום מהיר, שהיא כיום שיטה סטנדרטית, את תהליך ההתנתקות של טיפה. לנארד הראה כי תהליך התנתקות הטיפה מאופיין על ידי קיום צוואר ארוך ואסימטריה של חוט הנוזל המחזיק את הטיפה שהוא חד מאוד באזור הטיפה העיקרית ושטוח באזור הנחיר. תחילה החוט המשני מתנתק קרוב לטיפה העיקרית ,אך לפני שהחוט המשני מספיק לחזור חזרה לכיוון הנחיר הוא מתנתק גם בצד של הנחיר ונוצרת טיפת לוויין.

עם התפתחות עולם המחשוב התחילו להשתמש בסימולציות נומריות להבנת תהליך שבירת חוט זורם, אך פתרון משוואת נאוויה-סטוקס הכללית בזמן אינה בעיה פשוטה. בבעיות של שבירת חוט זורם החומר יכול להתנתק ולהתחבר מחדש ולכן המעקב אחרי השפה וההתמודדות עם נקודות סינגולריות הופך למאתגר עוד יותר. פעמים רבות למרות קיומן של הפרעות גדולות ניתן לפשט את משוואות נאוויה סטוקס ולקבל משוואות אותן ניתן לפתור בשיטות אסימפטוטיות הכוללות בין השאר אנליזה מרובת סקאלות ,התאמה אסימפטוטית, ושיטות פרטובציית תחום ואו באופן נומרי בעזרת שיטת אלמנטי השפה עבור גיאומטריות מורכבות כפי שעשו דומרמוט' ויו כאשר הרחיבו את השיטה הלגרנגיאנית למחצה לגופים אנכיים אקסיסימטריים בעלי שפה חופשית תוך הנחת זרימה פונציאלית ושולץ כאשר השתמש בקירוב דומה כשחקר התנהגות של מזרקה קפילרית, יאנגרן ואקריבוס כאשר חקרו את ההתנהגות של בועה בזרימת סטוקס וסטון וליל כאשר הרחיבו עבודה זו על מנת להתחשב ברלקסציה ושבירה של טיפה מוארכת. עבור מקרים בהם לא מצליחים למצוא קירוב אסימפטוטי נדרש לבצע סימולציות נומריות מלאות על ידי שיטות שיודעות להתמודד עם שפות חופשיות כמו שיטת נפח הנוזל ושיטת סט מפולס, אנליזה שכזו בוצעה על ידי פורם והתמקדה בטכנולוגיית ההדפסה "טיפה לפי דרישה" בעזרת שיטת ההפרשים הסופיים.

המנגנון הפיזיקלי

המנגנון הפיזיקלי לשבירת חוט זורם

עבור חוט זורם נייח תהליך השבירה מתחיל עם הגברה של הפרעות קטנות , תהליך זה מתואר על ידי התיאוריה הלינארית לשבירת חוט זורם. בכל זורם תמיד קיימות הפרעות קטנות והן נוצרות ממקורות רבים כמו למשל רעידות במיכל ממנו יוצא הזורם ואו חוסר אחידות בפתח ממנו יוצא הזורם. הפרעות כלליות קשות לאפיון ,אך עבור מערכות לינאריות ניתן להשתמש בהפרדת משתנים ובעזרת טור פוריה מוכלל לפרק את ההפרעה להפרעות שונות ובלתי תלויות. במקרה של חוט זורם נייח מתקבל כי מדובר בטור טור פורייה המתואר על ידי סינוסים וקוסינוסים וכך ניתן לפרק את ההפרעה לכניסות בעלות מספרי גל שונים ולבחון עבורם את הגדילה ואו הדעיכה בזמן.

ניתן להשתמש בעובדה שזורמים נעים מלחץ גבוה ללחץ נמוך על מנת לבחון את הדעיכה ואו הגדילה של אורך הגל בחוט הזורם.

נגדיר את המשטח $S$ של חוט הזורם על ידי:$S=r-(r_{0}+h)=r-(r_{0}+\epsilon sin(kz))$

כאשר $r_{0}$ הוא רדיוס החוט במצב הבסיס לפני כניסת ההפרעה , $r$ הוא רדיוס הנוכחי, $h=\epsilon sin(kz)$ היא ההפרעה ברדיוס החוט, $k$ הוא מספר הגל, $z$ הוא הציר האורכי ו-$\epsilon$ היא האמפליטודה של ההפרעה אשר הנחנו שהיא קטנה.

נסתכל על שיווי המשקל הנורמלי בממשק בין חוט הזורם לבין הזורם החיצוני לו במערכת צירים גלילית ונניח כי מתח הפנים קבוע ונקבל $\left(p_{I}-p_{E}+\left(\left(\tau _{E}-\tau _{I}\right)\cdot {\hat {n}}\right)\cdot {\hat {n}}\right)_{r=r_{0}+\epsilon sin(kz)}=\left(\sigma \nabla \cdot {\hat {n}}\right)_{r=r_{0}+\epsilon sin(kz)}$

כאשר$p_{I}$ שהוא הלחץ בחוט, $p_{E}$ שהוא הלחץ בזורם החיצוני, $\tau _{I}$ הוא מאמץ הגזירה בחוט, $\tau _{E}$ הוא מאמץ הגזירה בזורם החיצוני, $\sigma$ הוא מתח הפנים, ${\hat {n}}$ הוא הנורמל למשטח, $\nabla \cdot {\hat {n}}$ הוא פעמיים העקמומיות הממוצעת של המשטח $H$.

לשם פשטות נניח כי ההפרעות הינן אקסיסימטריות כלומר לא תלויות ב-$\phi$. כמו כן נגדיר את ההטרחה בממשק בכיוון $-{\hat {r}}$ באופן הבא: $T=p_{I}-p_{E}+{\tau _{rr}}_{E}-{\tau _{rr}}_{I}$

נחשב את הנורמל למשטח $S$ במערכת קוארדינטות גלילית בעזרת אופרטור הגרדיאנט במערכת גלילית ונקבל: ${\hat {n}}={\frac {\nabla S}{|\nabla S|}}={\frac {{\frac {\partial S}{\partial r}}{\hat {r}}+{\frac {1}{r}}{\frac {\partial S}{\partial \phi }}{\hat {\phi }}+{\frac {\partial S}{\partial z}}{\hat {z}}}{\left(\left({\frac {\partial S}{\partial r}}\right)^{2}+\left({\frac {1}{r}}{\frac {\partial S}{\partial \phi }}\right)^{2}+\left({\frac {\partial S}{\partial z}}\right)^{2}\right)^{\frac {1}{2}}}}={\frac {1{\hat {r}}-{\frac {\partial h}{\partial z}}{\hat {z}}}{\left(1+\left({\frac {\partial h}{\partial z}}\right)^{2}\right)^{\frac {1}{2}}}}\approx 1{\hat {r}}-k\epsilon cos(kz){\hat {z}}$

כאשר ${\hat {r}}$ הוא וקטור יחידה בכיוון הציר הרדיאלי ו-${\hat {z}}$ הוא וקטור יחידה ביכוון הציר האורכי.

כמו כן תוך שימוש באופרטור הדיברגנץ במערכת קוארדינטות גלילית נקבל כי:

$\left(\nabla \cdot {\hat {n}}\right)_{r=r_{0}+\epsilon sin(kz)}=\left({\frac {1}{r}}\left({\frac {\partial r{\hat {n}}_{r}}{\partial r}}\right)+{\frac {1}{r}}{\frac {\partial {\hat {n}}_{\phi }}{\partial \phi }}+{\frac {\partial {\hat {n}}_{z}}{\partial z}}\right)_{r=r_{0}+\epsilon sin(kz)}$

$=\left({\frac {1}{r\left(1+\left({\frac {\partial h}{\partial z}}\right)^{2}\right)^{\frac {1}{2}}}}-{\frac {\frac {\partial ^{2}h}{\partial z^{2}}}{\left(1+\left({\frac {\partial h}{\partial z}}\right)^{2}\right)^{\frac {1}{2}}}}+{\frac {\left({\frac {\partial h}{\partial z}}\right)^{2}{\frac {\partial ^{2}h}{\partial z^{2}}}}{\left(1+\left({\frac {\partial h}{\partial z}}\right)^{2}\right)^{\frac {3}{2}}}}\right)_{r=r_{0}+\epsilon sin(kz)}$

$={\frac {1}{\left(r_{0}+\epsilon sin(kz)\right)\left(1+\epsilon ^{2}k^{2}\left(cos(kz)\right)^{2}\right)^{\frac {1}{2}}}}+{\frac {\epsilon k^{2}sin(kz)}{\left(1+\epsilon ^{2}k^{2}\left(cos(kz)\right)^{2}\right)^{\frac {1}{2}}}}-{\frac {\left(\epsilon kcos(kz)\right)^{2}\epsilon k^{2}sin(kz)}{\left(1+\epsilon ^{2}k^{2}\left(cos(kz)\right)^{2}\right)^{\frac {3}{2}}}}$

$\approx {\frac {1}{r_{0}}}-{\frac {\epsilon sin(kz)}{r_{0}^{2}}}+\epsilon k^{2}sin(kz)+O(\epsilon ^{2})$

נציב חזרה בתוך תנאי השפה עבור המאמץ הנורמלי ונקבל:

$T={\frac {\sigma }{r_{0}}}+\sigma \left(-{\frac {\epsilon }{r_{0}^{2}}}+\epsilon k^{2}\right)sin(kz)$

נניח כי במצב זה המערכת בשיווי משקל סטטי ולכן:$T=p_{I}-p_{E}={\frac {\sigma }{r_{0}}}+\sigma \left(-{\frac {\epsilon }{r_{0}^{2}}}+\epsilon k^{2}\right)sin(kz)$

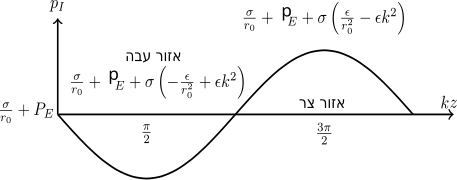
עבור $k$ מספיק קטן נצייר את הגרף עבור הלחץ בתוך החוט $p_{I}$ כאשר נניח כי הלחץ החיצוני קבוע.

רדיוסי עקמומיות בחוט זורם העובר תהליך פירוק. כחול מייצג את רדיוס העקמומיות הראשון ואדום את רדיוס העקמומיות השני במקומות הדלים והמעובים.

מהגרף מתקבל שהתנאי היחיד לשיווי משקל הינו כאשר $kr_{0}=1$.

אם מתקיים $kr_{0}<1$ הלחץ באזור הצר גדול יותר כלומר זורם יעבור לאזור העבה ומתקבלת אי יציבות.

אם מתקיים $kr_{0}>1$ הלחץ באזור הצר קטן יותר ולכן זורם יעבור לאזור הצר והזורם יחזור לשיווי משקל.

עבור מצב סטטי את תנאי השפה למאמץ נורמלי ניתן לכתוב גם באופן הבא:

$p_{I}-p_{E}={\frac {\sigma }{r_{0}}}+\sigma \left(-{\frac {\epsilon }{r_{0}^{2}}}+\epsilon k^{2}\right)sin(kz)=2\sigma H=\sigma \left({\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}\right)$ כאשר $R_{1}$ הוא רדיוס העקמומיות הראשון ו-$R_{2}$ הוא רדיוס העקמומיות השני ביחס ל-2 צירים מאונכים. רדיוסי העקמומיות מוגדרים להיות חיוביים כאשר אם נשלים את המעגל שלהם נעטוף חומר נוסף מאותו סוג. אם נגדיר את הצירים האורתוגונליים בתור הציר האורכי והציר הרדיאלי נקבל כי האזור הצר עבור אורך גל הגדול מ-$\lambda >{\frac {2\pi }{k}}=2\pi r_{0}$ יהיה עם לחץ גבוה יותר ותתקבל אי יציבות.

נסיק כי עבור הפרעות אינפיניטסימליות אקסיסימטריות אורך הגל של ההפרעה קובע את יציבות חוט הזורם ,עקב כך שעבור הפרעה אינפיניטסימלית כללית קיימים כל מספרי הגל בו זמנית מתקבל כי קירוב טוב בדר"כ לאורך הגל אשר יוביל לשבירת חוט הזורם הינו אורך הגל המוביל לתדר $\omega$ החיובי הגדול ביותר.

תהליך דומה ניתן לבצע כאשר ההפרעה הינה $\epsilon cos(kz)$ , אך כאשר מוסיפים הפרעה בציר $\phi$ וכבר לא מדובר בהפרעה אקסיסימטרית נדרשת אנליזה דינאמית מלאה ,אך לפחות עבור זורם ניוטוני בלתי דחיס התוצאה נשארת זהה ומתקבל שההפרעות אינפיניטסימליות בציר $\phi$ מייצבות את חוט הזורם.

באנליזה זו לא הנחנו על הזורם שהוא בלתי דחיס ואו ניוטוני ,אך כן השתמשנו בצורת הגליל של הממשק בין הזורמים ולכן אנליזה זו תקפה עבור ממשק גלילי בין 2 זורמים.

התנהגות לא לינארית

התיאוריה לאי יציבות לינארית שפיתח ריילי מאפשרת לתאר את חוט הזורם כאשר ההפרעות הינן קטנות ותהליך השבירה של חוט הזורם רק מתחיל , אך כאשר ההפרעות גודלות מספיק תופעות לא לינאריות משפיעות על תהליך שבירת החוט וכתוצאה מכך על כמות יחידות הנוזל שנוצרות וגודלן.

מבחינה ניסויית פליקס סבר הבחין בקיום טיפות לוויין בתחום הסילון ופיליפ לנארד הבחין בקיום טיפות לוויין בתחום הטפטוף , מכך ניתן להסיק שעבור התהליך הלא לינארי הכללי התנתקות הטיפה הינה תהליך אוניברסאלי בעלת דמיות עצמית, מבחינה תיאורטית ניתן להסביר זאת על ידי כך שבסינגולריות אין סקלת אורך אופיינית.

במקרה הפשוט ביותר ניתן לקרב את החוט כחד מימדי התלוי בציר האורכי $z$ ובזמן $t$ , במצב זה נגדיר את המשתנים חסרי המימד $z'={\frac {z-z_{0}}{L_{v}}}$ וכמו כן $t'={\frac {t_{0}-t}{t_{v}}}$ כאשר $L_{v}$ ו-$t_{v}$ הינם גדלים אופיינים לציר האורכי ולזמן בהתאמה ו-$z_{0}$ ו-$t_{0}$ מהווים את הנקודה הסינגולרית בה הטיפה מתנתקת.

עקב סימילריות נקבל שהפתרון הוא מהצורה: $r(z,t)=L_{v}|t'|^{\alpha _{1}}\phi (\xi )$ , $v(z,t)={\frac {L_{v}}{t_{v}}}|t'|^{\alpha _{2}}\psi (\xi )$ , $\xi ={\frac {z'}{t'^{\beta }}}$ כאשר $r$ מייצג את רדיוס החוט הכולל את ההפרעה , $v$ את המהירות הצירית, $\alpha _{1}$,$\alpha _{2}$,$\beta$ הינם קבועים המייצגים את המאזן בין התופעות השונות בבעיה ו-$\phi (\xi )$,$\psi (\xi )$ הן פונקציות כלשהן.

מספרים חסרי מימד

כאשר תהליך שבירת חוט הזורם נובע מאי יציבות קפילרית עבור חוט זורם סטטי הנמצא בריק, מתוך משוואת-נאוויה סטוקס יחד עם תנאי השפה הקינמטי ותנאי השפה עבור המאמץ הנורמלי בממשק בין הזורם לריק מתקבל כי ניתן לאפיין את הזורם על ידי 4 מספרים חסרי מימד בהם מספר ובר , המספר הקפילרי ומספר בונד אליהם נדרש להוסיף את מספר הגל המנורמל של ההפרעה . בחירת מספרים חסרי מימד אינה יחידה ולעיתים בספרות נוהגים להחליף את מספר ובר ואת המספר הקפילרי במספר אונסורג' ומספר ריינולדס. בהינתן מקרה מורכב יותר ניתן להשתמש במשפט פאי של בקינגהאם ואו לנרמל את המשוואות השולטות ישירות תוך בחירת סקאלות מתאימות לתיאור הבעיה. כאשר רדיוס החוט קטן מספיק מספר בונד זניח וניתן לתאר את הבעיה ללא השפעות כבידה.

עבור חוט זורם עם ערכים קטנים של המספר הקפילי ושל מספר בונד וכאשר מספר ובר הינו מסדר גודל אחד מתקבל כי האינרציה שולטת בבעיה וניתן לאפיין את התדר העצמי כפונקציה של מספר ובר ומספר הגל המנורמל של ההפרעה. עבור חוט זורם עם ערכים קטנים של מספר ובר ושל מספר בונד וכאשר המספר הקפילרי הינו מסדר גודל של אחד מתקבל כי צמיגות שולטת בבעיה ואת התדר העצמי ניתן לתאר על ידי המספר הקפילרי ומספר הגל המנורמל של ההפרעה.

מקרים פרטיים

יציבות לינארית של חוט זורם נייח בלתי צמיג בריק

בשנת 1879 פתר ריילי בקירוב מסדר ראשון את הבעיה של זורם נייח, בלתי דחיס וניוטוני בתוך ריק כאשר המספר הקפילרי $Ca<<1$ , מספר בונד $Bo<<1$ ומספר ובר הינו $We=O(1)$.

תיאור זה שקול למעשה למצב בו חוט הזורם הינו בלתי צמיג וניתן להזניח את כוחות הכבידה.

מתוך אנליזה מימדית עבור מקרה זה מתקבל כי הפתרון תלוי ב-2 מספרים חסרי מימד והם מספר ובר $We$ ומספר הגל המנורמל $x=kr_{0}$.

מספר ובר ניתן לביטוי על ידי $We={\frac {\rho v_{v}^{2}L_{v}}{\sigma }}$ כאשר האורך האופייני $L_{v}=r_{0}$ וכמו כן $v_{v}$ הינה המהירות האופיינית ולכן נרמול חסר המימד שנבחר כדי להפוך את מספר ובר ל-1 הינו $v_{v}={\sqrt {\frac {\sigma }{\rho r_{0}}}}$.

נגדיר את הקירוב האסימפטוטי:

$v_{r}={v_{r}}_{0}+\epsilon {v_{r}}_{0}+O(\epsilon ^{2})$ , $v_{z}={v_{z}}_{0}+\epsilon {v_{z}}_{0}+O(\epsilon ^{2})$ , $p=p_{0}+\epsilon p_{1}+O(\epsilon ^{2})$ ,$h=\epsilon h_{1}+O(\epsilon ^{2})$

כאשר $h$ ההפרעה בציר הרדיאלי ,$p$ הלחץ , $v_{z}$ המהירות בציר האורכי ו-$v_{r}$ המהירות בציר הרדיאלי.

נציב אותו בתוך משוואות נאוויה סטוקס ומשוואת שימור המסה במערכת קואורדינטות גלילית , וכמו כן בתנאי השפה הקינמטי לפיו המהירות הנורמלית הינה אפס ותנאי השפה עבור המאמץ נורמאלי.

כאשר לוקחים את הקירוב מסדר אפס מקבלים את פתרון הבסיס הידוע ${u_{r}}_{0}=0,{u_{z}}_{0}=0,p_{0}={\frac {\sigma }{r_{0}}}$.

לאחר מכן לוקחים את הקירוב מסדר ראשון ומתקבלת מערכת משוואות דיפנציאליות חלקית אותה פותרים על ידי הפרדת משתנים כאשר מקבלים בהתאם

לאנליזת יציבות מודאלית דעיכה או ההגברה אקספוננציאלית בזמן בהתאם לתדר $\omega$.

פתרון מערכת המשוואות מביא ליחס הנפיצה אותו מצא ריילי:

$\omega ^{2}={\frac {\sigma }{\rho r_{0}^{3}}}kr_{0}\left(1-k^{2}r_{0}^{2}\right){\frac {I_{1}(kr_{0})}{I_{0}(kr_{0})}}$

כאשר $I_{0},I_{1}$ הינן פונקציות בסל המתוקנות מהסוג הראשון מסדר אפס וסדר אחד.

$x=kr_{0}$ מספר הגל המנורמל, $k$ מספר הגל, $r_{0}$ רדיוס החוט במצב הבסיס , $\sigma$ מתח הפנים ו-$\rho$ צפיפות חוט הזורם.

הביטוי שהתקבל הינו תמיד חיובי כאשר $kr_{0}<1$ והאי יציבות המקסימאלית שלו מתקבלת ב-$kr_{0}=0.697$ שזה שקול לאורך הגל $\lambda ={\frac {2\pi }{k}}=9.01r_{0}$

יציבות לינארית של חוט זורם נייח בתוך זורם חיצוני

בשנת 1892 ג'ון ריילי הרחיב את הפתרון שמצא קודם לכן עבור זורם ניוטוני בלתי דחיס עם אינרציה זניחה ולאחר מכן בשנת 1935 טומוטיקה הרחיב פתרון זה עבור חוט זורם נייח בתוך זורם אחר כאשר 2 הזורמים הם ניוטונים ובלתי דחיסים. טומוטיקה השתמש בקירוב האסימפטוטי:

$\psi =\psi _{0}+\epsilon \psi _{1}+O(\epsilon ^{2})$ ,$p=p_{0}+\epsilon p_{1}+O(\epsilon ^{2})$ , $h=\epsilon h_{1}+O(\epsilon ^{2})$.

כאשר פונקציית הזרם של סטוקס לקואורדינטות גליליות $\psi$ מוגדרת באופן הבא:

$u_{r}={\frac {1}{r}}{\frac {\partial \psi }{\partial z}}$ , $u_{z}=-{\frac {1}{r}}{\frac {\partial \psi }{\partial r}}$ , $u=\nabla \times B$ , $B=-{\frac {\psi }{r}}{\hat {\phi }}$

עבור המקרה הדו מימדי כאשר לוקחים את הקירוב מסדר אפס מתקבל מצב הבסיס הידוע ${{u_{r}}_{I}}_{0}=0,{{u_{z}}_{I}}_{0}=0,{{u_{r}}_{E}}_{0}=0,{{u_{z}}_{E}}_{0}=0,{p_{I}}_{0}-{p_{E}}_{0}={\frac {\sigma }{r_{0}}}$

כאשר $I$ מציין את החוט (הזורם הפנימי) ו-$E$ מייצג את הזורם החיצוני.

לאחר הצבת פונקציית הזרם בתוך משוואת הערבוליות ${\frac {Dw}{Dt}}=w\cdot \nabla u+\nu \nabla ^{2}w$ כאשר ${\frac {D}{Dt}}$ הינה הנגזרת החומרית ולקיחת הקירוב מסדר ראשון מתקבלת המשוואה איתה התחיל טומוטיקה את הפתרון $\left(D-{\frac {1}{\nu }}{\frac {\partial }{\partial t}}\right)D\psi _{1}=0$ כאשר $\nu$ היא הצמיגות הקינמטית והאופרטור הדיפרנציאלי הינו$D={\frac {\partial ^{2}}{\partial r^{2}}}-{\frac {1}{r}}{\frac {\partial }{\partial r}}+{\frac {\partial ^{2}}{\partial z^{2}}}$ , את המשוואה פתר טומוטיקה עבור הזורם החיצוני ועבור הזורם הפנימי.

לאחר פתרון המשוואה הזו ושימוש בכך שבתחום הפתרון אין נקודות סינגולריות , יחד עם ארבעת תנאי השפה שהם: מהירות נומלית זהה ואי החלקה בממשק בין 2 הזורמים, שיווי משקל מאמץ נורמלי ומשיקי תוך שימוש במשוואות נאוויה סטוקס כדי לקבל את הלחצים טומוטיקה הצליח לקבל פתרון כללי עבורו חילץ את יחס הנפיצה.

${\begin{vmatrix}I_{1}(kr_{0})&I_{1}({k_{*}}_{I}r_{0})&K_{1}(kr_{0})&K_{1}({k_{*}}_{E}r_{0})\\r_{0}kI_{0}(kr_{0})&r_{0}{k_{*}}_{I}I_{0}({k_{*}}_{I}r_{0})&-r_{0}kK_{0}(kr_{0})&-r_{0}{k_{*}}_{E}K_{0}({k_{*}}_{E}r_{0})\\2{\frac {\mu _{I}}{\mu _{E}}}k^{2}I_{1}(kr_{0})&{\frac {\mu _{I}}{\mu _{E}}}\left(k^{2}+({k_{*}}_{I})^{2}\right)I_{1}({k_{*}}_{I}r_{0})&2k^{2}K_{1}(kr_{0})&\left(k^{2}+({k_{*}}_{E})^{2}\right)K_{1}({k_{*}}_{E}r_{0})\\F_{1}&F_{2}&F_{3}&F_{4}\\\end{vmatrix}}=0$

כאשר:

$F_{1}=2ik^{2}{\frac {\mu _{I}}{\mu _{E}}}I_{1}'(kr_{0})-{\frac {\rho _{I}\omega }{\mu _{E}i}}I_{0}(kr_{0})+{\frac {\sigma ik}{\mu _{E}r_{0}^{2}\omega }}\left(k^{2}r_{0}^{2}-1\right)I_{1}(kr_{0})$

$F_{2}=2ik{k_{*}}_{I}{\frac {\mu _{I}}{\mu _{E}}}I_{1}'({k_{*}}_{I}r_{0})+{\frac {\sigma ik}{\mu _{E}r_{0}^{2}\omega }}\left(k^{2}r_{0}^{2}-1\right)I_{1}({k_{*}}_{I}r_{0})$

$F_{3}={\frac {\rho _{E}\omega }{\mu _{E}i}}K_{0}(kr_{0})+2ik^{2}K_{1}'(kr_{0})$

$F_{4}=2ik{k_{*}}_{E}K_{1}'({k_{*}}_{E}r_{0})$

${k_{*}}_{E}^{2}=k^{2}+{\frac {\omega }{\nu _{E}}}$, ${k_{*}}_{I}^{2}=k^{2}+{\frac {\omega }{\nu _{I}}}$

ו-$'$ מסמן את הנגזרת הראשונה לפי הביטוי בתוך הסוגריים למשל $K_{1}'(x)={\frac {dK_{1}(x)}{dx}}$.

זורמים מאוד צמיגים

כאשר לוקחים את המקרה הכללי של חוט זורם נייח בתוך זורם חיצוני עם זורמים ניוטונים ובלתי דחיסים ומציבים בתוכו אינרציה זניחה לאחר קירוב כלל הביטויים התלויים בצפיפות סביב מספר הגל $k$ וביצוע מספר פעולות שורה ועמודה בדטרמיננטה ,משאיפים את הצפיפות לאפס ופותחים הדטרמיננטה לפי השורה הרביעית ומתקבל יחס הנפיצה אותו מצא טומוטיקה למקרה זה:

$\omega ={\frac {\sigma }{2r_{0}\mu _{E}}}\left(1-x^{2}\right)\Phi (x)$

כאשר $x=kr_{0}$ ו-$\Phi (x)$ נתון על ידי הביטוי:

$\Phi (x)={\frac {N(x)}{D(x)}}$

$N(x)=I_{1}(x)\Delta _{1}-\left(xI_{0}(x)-I_{1}(x)\right)\Delta _{2}$

$D={\frac {\mu _{I}}{\mu _{E}}}\left(xI_{0}(x)-I_{1}(x)\right)\Delta _{1}-{\frac {\mu _{I}}{\mu _{E}}}\left((x^{2}+1)I_{1}(x)-xI_{0}(x)\right)\Delta _{2}$

והמקדמים $\Delta _{1},\Delta _{2},\Delta _{3},\Delta _{4}$ נתונים על ידי:

$\Delta _{1}={\begin{vmatrix}xI_{0}(x)-I_{1}(x)&K_{1}(x)&-xK_{0}(x)-K_{1}(x)\\I_{0}(x)+xI_{1}(x)&-K_{0}(x)&-K_{0}(x)+xK_{1}(x)\\{\frac {\mu _{I}}{\mu _{E}}}xI_{0}(x)&K_{1}(x)&-xK_{0}(x)\\\end{vmatrix}}$

$\Delta _{2}={\begin{vmatrix}I_{1}(x)&K_{1}(x)&-xK_{0}(x)-K_{1}(x)\\I_{0}(x)&-K_{0}(x)&-K_{0}(x)+xK_{1}(x)\\{\frac {\mu _{I}}{\mu _{E}}}I_{1}(x)&K_{1}(x)&-xK_{0}(x)\\\end{vmatrix}}$

$\Delta _{3}={\begin{vmatrix}I_{1}(x)&xI_{0}(x)-I_{1}(x)&-xK_{0}(x)-K_{1}(x)\\I_{0}(x)&I_{0}(x)+xI_{1}(x)&-K_{0}(x)+xK_{1}(x)\\{\frac {\mu _{I}}{\mu _{E}}}I_{1}(x)&{\frac {\mu _{I}}{\mu _{E}}}xI_{0}(x)&-xK_{0}(x)\\\end{vmatrix}}$

$\Delta _{4}={\begin{vmatrix}I_{1}(x)&xI_{0}(x)-I_{1}(x)&K_{1}(x)\\I_{0}(x)&I_{0}(x)+xI_{1}(x)&-K_{0}(x)\\{\frac {\mu _{I}}{\mu _{E}}}I_{1}(x)&{\frac {\mu _{I}}{\mu _{E}}}xI_{0}(x)&K_{1}(x)\\\end{vmatrix}}$

כאשר פותרים מקרה זה עבור יחס צמיגות ספציפי מתקבלת אי יציבות עבור $kr_{0}<1$ ואי היציבות מקסימלית מתקבלת כאשר ${\frac {\mu _{I}}{\mu _{E}}}\approx 0.28$.

מספר הגל המנורמל המקסימלי במקרה זה הינו $kr_{0}=0.59$ שזה שקול לאורך הגל $\lambda ={\frac {2\pi }{k}}=10.65r_{0}$.

צמיגות החוט הרבה יותר גדולה מהצמיגות של הסביבה

עבור מקרה זה לוקחים את הפתרון עבור זורמים מאוד צמיגים , מכפילים את $N$ ואת $D$ ב-$D={\frac {\mu _{E}}{\mu _{I}}}$ ומוציאים מ-${\frac {\mu _{I}}{\mu _{E}}}$ כגורם משותף , לאחר שמשאיפים את ${\frac {\mu _{E}}{\mu _{I}}}$ לאפס מתקבל הפתרון הבא:

$\omega ={\frac {\sigma \left(x^{2}-1\right)}{2r_{0}\mu _{I}}}{\frac {1}{(x^{2}+1)-x^{2}{\frac {(I_{0}(x))^{2}}{(I_{1}(x))^{2}}}}}$

כאשר $I_{0},I_{1}$ הינן פונקציות בסל המתוקנות מהסוג הראשון מסדר אפס וסדר אחד.

$x=kr_{0}$ מספר הגל המנורמל, $k$ מספר הגל, $r_{0}$ רדיוס החוט במצב הבסיס , $\sigma$ מתח הפנים ו-$\mu _{I}$ צמיגות חוט הזורם. פתרון זה הינו הפתרון אותו מצא ריילי בשנת 1892, הביטוי שהתקבל הינו תמיד חיובי כאשר $kr_{0}<1$ ואורך הגל המוביל לאי יציבות המקסימלית יוצא $\infty$, המשמעות של פתרון זה הינה ההבנה שצמיגות גדולה מאוד אינה משנה את התדרים הלא יציבים אלא רק מאטה את קצב הגדילה של ההפרעה.

צמיגות הסביבה הרבה יותר גדולה מצמיגות החוט

עבור המקרה בו צמיגות הסביבה הרבה יותר גדולה מצמיגות החוט לוקחים את הפתרון עבור זורמים מאוד צמיגים , ומשאיפים את ${\frac {\mu _{I}}{\mu _{E}}}$ לאפס מתקבל הפתרון הבא:

$\omega ={\frac {\sigma \left(x^{2}-1\right)}{2r_{0}\mu _{E}}}{\frac {1}{(x^{2}+1)-x^{2}{\frac {(K_{0}(x))^{2}}{(K_{1}(x))^{2}}}}}$

כאשר $K_{0},K_{1}$ הינן פונקציות בסל המתוקנות מהסוג השני מסדר אפס וסדר אחד.

$x=kr_{0}$ מספר הגל המנורמל, $k$ מספר הגל, $r_{0}$ רדיוס החוט במצב הבסיס , $\sigma$ מתח הפנים ו-$\mu _{E}$ צמיגות הזורם החיצוני.

הביטוי שהתקבל הינו תמיד חיובי כאשר $kr_{0}<1$ ואורך הגל המוביל לאי יציבות המקסימלית יוצא $\infty$, המשמעות של פתרון זה הינה ההבנה שצמיגות גדולה מאוד אינה משנה את התדרים הלא יציבים אלא רק מאטה את קצב הגדילה של ההפרעה.

זורמים עם אינרציה גדולה

ברגע שמציבים צמיגות זניחה מתקבל כי המשוואה אותה נדרש לפתור הינה ${\frac {\partial }{\partial t}}D\psi _{1}=0$ בלבד.

ולכן מתוך הפתרון של טומוטיקה אשר הורכב מפתרון ל-2 המשוואות: ${\frac {\partial }{\partial t}}D\psi _{1}=0$, $\left(D-{\frac {1}{\nu }}{\frac {\partial }{\partial t}}\right)\psi _{1}=0$ נוכל לאפס את האיברים הקשורים לפתרון השני וכתוצאה מכך העמודות השנייה והרביעית בפתרון הכללי יתאפסו.

בנוסף עקב כך שהצמיגות זניחה נקבל כי תנאי השפה הרלוונטים הינם תנאי השפה הקינמטי לפיו המהירות הנורמלית בממשק זהה עבור 2 הזורמים ותנאי השפה עבור המאמץ נורמאלי.

מכך ניתן להסיק כי ניתן לאפס את השורות השנייה והשלישית מתוך הדטרמיננטה של הפתרון הכללי המייצגות את תנאי השפה עבור אי החלקה בממשק בין 2 הזורמים ותנאי השפה עבור מאמץ הגזירה.

כעת אם נפתור דטרמיננטה זו נקבל $\omega ^{2}={\frac {\sigma }{\rho _{E}r_{0}^{3}}}x\left(1-x^{2}\right){\frac {1}{{\frac {\rho _{I}}{\rho _{E}}}{\frac {I_{0}(x)}{I_{1}(x)}}+{\frac {K_{0}(x)}{K_{1}(x)}}}}$

כאשר $I_{0},I_{1}$ הן פונקציות בסל המתוקנות מהסוג הראשון מסדר אפס ומסדר אחד.

$K_{0},K_{1}$ הן פונקציות בסל המתוקנות מהסוג השני מסדר אפס ומסדר אחד.

$x=kr_{0}$ מספר הגל המנורמל, $k$ מספר הגל, $r_{0}$ רדיוס החוט במצב הבסיס , $\sigma$ מתח הפנים ,$\rho _{I}$ צפיפות חוט הזורם ו-$\rho _{E}$ צפיפות הזורם החיצוני.

הביטוי שהתקבל הינו תמיד חיובי כאשר $kr_{0}<1$ והאי יציבות המקסימאלית שלו מתקבלת ב-$kr_{0}=0.697$ (מתקבל כאשר $\rho _{I}\rightarrow \infty$) שזה שקול לאורך הגל $\lambda ={\frac {2\pi }{k}}=9.01r_{0}$.

ניתן לשים לב שניתן לקבל מהפתרון הזה מידית קירוב נוסף כאשר הצפיפות החיצונית הרבה יותר גדולה מהצפיפות הפנימית ואז מתקבל: $\omega ^{2}={\frac {\sigma }{\rho _{E}r_{0}^{3}}}kr_{0}\left(1-k^{2}r_{0}^{2}\right){\frac {K_{1}(kr_{0})}{K_{0}(kr_{0})}}$ , אי היציבות המקסימאלית במקרה זה מתקבלת עבור $kr_{0}=0.484$ שזה שקול לאורך הגל $\lambda ={\frac {2\pi }{k}}=12.98r_{0}$.

היווצרות טיפות לוויין

מים זורמים מברז כך שנוצרת טיפה אחת גדולה ומספר טיפות לוויין.

טיפות לוויין נוצרות מהיפרדות החוט המשני המחובר לטיפה מצד אחד ולשאר חוט הזורם מצדו השני. ההפרדה אינה במיקום בו העקמומיות מקסימאלית אלא מתקיימת בין ההפרעות בחוט המשני. אם בעת ההפרדה נוצרת הפרעה מתאימה אז החוט המשני יעבור התפרקויות נוספות ויווצרו מספר טיפות לוויין. יצירת טיפות לוויין הינה תופעה לא רצויה באפליקציות הדורשות דיוק ואחידות והיא תלויה בהתנהגות הדינאמית באזור חוט הזורם המשני בשלבים האחרונים לפני הניתוק.

רוטלנד וגיימסון ולאחר מכן לפרנס הראו שנפח טיפת הלוויין קטן עבור הגדלה של $x=kr_{0}$ כאשר $k$ הינו מספר הגל של ההפרעה ו-$r_{0}$ הינו רדיוס חוט הזורם. כאשר $x$ התקרב ל-0.2 עבור מים ול-0.3 עבור גליצרול התקבל שגודל טיפת הלוויין דומה לגודל הטיפה העיקרית אך כאשר $x$ מתקרב ל-0.7 המשיכו להתקבל טיפות לוויין בניגוד לתיאוריה.

דוגמאות

צמיגות הדבש גדולה מספיק ומנחיתה את קצב גדילת ההפרעות הלא יציבות כך שלא מספיקות להיווצר טיפות.

טפטוף מברז

בזמן שמים עוזבים את הברז , חוט הזורם עובר הצרה עד אשר טיפה ראשית נפרדת מהחוט, החוט המשני לא מספיק לחזור כלפי מעלה וכתוצאה מההפרעות שנוצרות מתפרק למספר טיפות לוויין קטנות.

בועות אוויר

כאשר אוויר נכנס למיכל נוזל , כמו אקווריום, חוט הזורם עובר הצרה באזורים מסויימים עד שנוצרות בועות , כאשר נושפים אוויר לתוך כוס מים נוצרות בועות באופן דומה.

ניסוי טיפת הזפת

ניסוי טיפת הזפת הינו ניסוי מפורסם המראה שקיימים חומרים מאוד צמיגים כך שביום יום הם נראים מוצקים אך למעשה הם נוזלים, הצמיגות של הזפת בניסוי כל כך גדולה שרק 9 טיפות נפלו מאז 1927.

טיפות דבש

עקב הצמיגות הגדולה של הדבש ההפרעות הלא יציבות הקיימות בשפה לא מספיקות לגדול וכתוצאה מכך מתקבלים חוטים ארוכים של דבש.

הערות שוליים

[[קטגוריה:מכניקת הזורמים]] [[קטגוריה:אי יציבות בזרימה]]