נקע (הנדסה)


נקע (אנגלית: Dislocation), בהקשר הנדסת חומרים, הוא סוג של פגם במבנה הגבישי של חומר. קיום הנקעים מהווה פתרון לבעיות שלא ניתן להן מענה על ידי המבנה הגבישי המושלם בחומר. כך למשל, מוסבר תהליך הדפורמציה הפלסטית בעזרת תנועת נקעים בתוך החומר, וכן הולכה חשמלית. תכונות אלה תלויות גם בצפיפות הנקעים בגביש הנעה בין [1]. השפעת הנקעים על אלסטיות החומר פותחה בשנת 1905 על ידי ויטו וולטרה, ותנועת הנקעים בסדר גודל האטומי הוסברה על ידי סר ג'פרי טיילור בשנת 1934.
כישלון המבנה הגבישי המושלם[עריכת קוד מקור | עריכה]
המבנה הגבישי מתאר היטב את מבנה החומר, אולם תופעות אמפיריות שונות אינן עולות בקנה אחד עם התוצאות החזויות בעזרת המודל המושלם.
אלסטיות[עריכת קוד מקור | עריכה]
על פי התורה האלסטית, חומר הנתון תחת כוח משני קצותיו יעבור עיוות, אשר נתון ביחס ישר לכוח המופעל באופן הבא
כאשר A ו-L הם שטח הפאה ואורכו של החומר, F הכוח המופעל ו-Y מודול יאנג. בעזרת נוסחה זו ניתן להסיק על הכוח הדרוש לעיוות מסוים, אולם מדידות על חומרים הניבו ערכים קטנים מאלו התאורטיים עד כי בחלק מהחומרים השוני מגיע לסדר גודל של פי . השוואה בין מדידות נבחרות לערכן התאורטי ניתן לראות בטבלה 1. במציאות, הכוח שיש להפעיל כדי לצור עיוות בחומר קטן משמעותית מהכוח התאורטי - עובדה זו ניתנת להסבר על ידי קיומם של נקעים, המאפשרים עיוות של החומר על ידי תנועתם.
| חומר | מודול יאנג Y/5
|
כוח תאורטי
|
כוח מדוד
|
יחס |
|---|---|---|---|---|
| ברזל | 4.0 | 4 | 0.03 | 0.008 |
| טיטניום | 2.2 | 3.1 | 0.03 | 0.009 |
| סיליקון | 3.2 | 1.5 | 0.07 | 0.05 |
| זכוכית | 1.4 | 4 | 0.04 | 0.01 |
אי סדר גבישי בשני ממדים[עריכת קוד מקור | עריכה]
סדר ארוך טווח של המבנה הגבישי אינו מתקיים בחומרים דו־ממדיים, כיוון שהוא מופר על ידי פלקטואציות תרמיות של האטומים. נגדיר את סטיית המיקום של כל נקודה בגביש על ידי השדה הווקטורי כך שווקטור המיקום יינתן כך .
מכאן שהאנרגיה הפוטנציאלית של גביש דו־ממדי היא
C הוא קבוע בעל ממדים של אנרגיה ליחידת שטח.
על ידי התמרת פורייה של השדה הווקטורי , האנרגיה הפוטנציאלית תינתן כך
במעבר האחרון נעשה שימוש בהתמרת פורייה של פונקציית דלתא, כאשר V הנפח הדו־ממדי של המערכת.
בעזרת האנרגיה הפוטנציאלית ניתן לחשב את השונות בסטיית המיקום, כלומר השונות של השדה הווקטורי :
המיצוע התרמי יתבצע בסכימה על כל ערכי k עם התפלגות בולצמן, והאנרגיה הפוטנציאלית שחושבה מעלה.
בעזרת ביטוי זה נוכל לחשב את השונות
במעבר האחרון נעשה שימוש בפונקציית צפיפות המצבים במרחב התנע עבור גוף דו־ממדי.
השדה הווקטורי מתאר תנודות הגדולות ממרחק כלשהו D אשר גדול מהמרחק הבין-אטומי. לכן מתקיים התנאי עבור .
מכאן שהשונות תסתכם כך
האינטגרל מתבדר עבור k קטן, בתחום בו התורה האלסטית אמורה לשרת היטב. המשמעות היא שהסדר הגבישי אינו יכול להתקיים על פני סקאלות אורך גדולות.
כתוצאה מכך רק לאזורים קטנים בחומרסדר גבישי והם נפרדים זה מזה. ההפרדה תתקיים על ידי נקעים שיפרו את הסדר הגבישי.
המבנה הגאומטרי של נקעים[עריכת קוד מקור | עריכה]
כדי להבין את הגאומטריה של נקע, נשתמש במודל התלת-ממדי של המבנה המסודר של גביש, כאשר האטומים מיוצגים בעזרת כדורים. עבור נקע המצוי בסריג הגבישי, מוגדר ווקטור בורגרס - - המייצג את הנקע, ומציין את כיוון וגודל התקדמותו בחומר. בנוסף, מוגדר ווקטור קו הנקע , המקביל לציר הנקע ומפריד בין
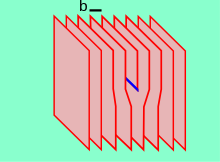
האזור של הגביש בו הסריג מושלם לבין האזור המושפע על ידי הנקע. על מנת למצוא את ווקטור בורגרס, יש להתבסס על כלל יד ימין כאשר ווקטור קו הנקע משמש כציר, ולסגור סביבו לולאה בעלת מספר קבוע של אתרי סריג בכל אחת מצלעותיה (איור 3). על הלולאה להשתרע רחוק מספיק מווקטור קו הנקע כך שהאטומים אותם היא מחברת נתונים בדפוס הסריג המושלם. עבור סריג אידיאלי ללא נקעים, נקודות ההתחלה והסיום של הלולאה יהיו באותו אתר סריג. אך אם הלולאה מקיפה נקע, יהיה הפרש בין נקודות ההתחלה והסיום של הלולאה. הפרש זה וכיוונו מהווים את ווקטור בורגרס.
בתוך כך מבדילים בין שני סוגים עיקריים של נקעים, אשר מהווים בסיס שלם וכל פגם מורכב מסוג יחיד או שניהם.

נקע קצה[עריכת קוד מקור | עריכה]
נקע קצה (באנגלית Edge dislocation) ניתן לתיאור על ידי הוספת חצי מישור עודף של אטומים לתוך מבנה הגביש, כאשר הוא גורם לעיוות מקומי של המישורים האטומיים מסביבו (איור 1). מכיוון שבאזור הנקע יש עודף מישורי גביש, מתקיים לחץ רב באזור זה. במקרה של הפעלת לחץ חיצוני, המישור העודף יתקדם דרך מישורי הגביש, כאשר הוא יוצר ומנתק קשרים עם מישורים אלה, עד שיגיע לגבול החיצוני של החומר. עבור נקע קצה וקטור בורגרס מאונך לוקטור קו הנקע כפי שמוצג באיורים 1 ו-3.
נקע בורג[עריכת קוד מקור | עריכה]
נקע בורג (Screw dislocation) מוגדר כאשר באזור שמעבר לוקטור קו הנקע חלה החלקה של אתרי הסריג בצדו האחד של מישור המקביל לווקטור קו הנקע, ביחס לאתרי הסריג שנמצאים מעבר למישור זה. צורה נוספת לחשוב על כך היא הוספת מישור של אתרי סריג מעל לחלק מהאתרים הקיימים (איור 2). באופן זה הלולאה הדמיונית מתחילה ומסתיימת בשני מישורים שונים ומכאן "צורת הבורג". במקרה זה ווקטור בורגרס מקביל לווקטור קו הנקע כפי שניתן לראות באיור 3.

תנועת נקעים בחומר[עריכת קוד מקור | עריכה]
בעת הפעלת כוח חיצוני, נשברים הקשרים בין האטומים המקיפים את הנקע לשכניהם הקרובים בגביש, ונוצרת אינטראקציה בינם לבין אטומים במישור סמוך. באופן זה הנקע מתקדם לאורך הגביש. הכוח הדרוש לשבירת הקשרים של אטום יחיד נמוך מזה הדרוש לשבירת הקשרים של סריג שלם, ולכן תנועת הנקעים הא הסיבה לכוח הנמוך הדרוש לעיוות החומר. תנועת הנקעים בחומר מתבצעת תוך החלקה של חלק מן הגביש ביחס לחלק אחר לאורך מישור הנקרא מישור ההחלקה. במקרה של נקע קצה מישור ההחלקה מאונך למישור העודף ומכיל את וקטור קו הנקע ווקטור בורגרס, וכיוון ההחלקה מקביל לווקטור בורגרס. במקרה של נקע בורג כיוון ההחלקה מאונך לווקטורי בורגרס וקו הנקע, ומישור ההחלקה נפרש על ידי כיוון ההחלקה ווקטור בורגרס[3]. בעת עיוות הגביש, הנקעים נעים לאורכו ואף גדלים תוך השפעת הכוח כך שייתכנו מרווחים גדולים של אתרי סריג ללא אטומים בגביש.
כאמור, התורה האלסטית של החומר והכוח הדרוש לעיוותו מתוקנים על ידי קיומם של נקעים. בעוד שתאורטית דרוש כוח רב כדי לעוות חומר בעל מבנה גבישי מושלם, בפועל דרוש כוח קטן יותר כדי לעוות את החומר - הכוח הדרוש להזזת הנקעים.
כדי למצוא כוח זה, נניח מודל של סריג חד־ממדי - שרשרת של מסות זהות המחוברות בקפיצים בעלי קבוע קפיץ k והנתונות בפוטנציאל פרבולי מחזורי בעל קבוע קפיץ (איור 4). על השרשרת מופעל כוח חיצוני f כך שהפוטנציאל הפרבולי המחזורי הוא
a הוא המרחק בין המסות בעת שיווי משקל. הכוח הפועל על המסה n הוא
כעת בהינתן נקע בחומר, אחת המסות חסרה. ללא הגבלת הכלליות ניתן להניח כי בור הפוטנציאל במיקום n=0 ריק, כך שהמסה 0 נתונה בבור והמסה 1 נתונה בבור . מכאן שהכוח על מסה n הוא
בשיווי משקל הכוח השקול מתאפס כך שהפתרונות לשתי המשוואות הם
על ידי הצבת הפתרונות במשוואות הכוחות, וכן השוואת שני הפתרונות עבור המיקומים n=0,1 נקבל

כאשר הכוח החיצוני המופעל גדול מספיק, מסה 0 הנתונה בשיווי משקל במיקום תתגבר על בור הפוטנציאל ותנוע מעבר למיקום כך שהנקע, כלומר בור הפוטנציאל הריק, ינוע בכיוון זה גם הוא.
כוח קריטי זה יחושב על ידי הפתרון עבור
הכוח המקסימלי הדרוש להזזת המסות ממקומן אל בור הפוטנציאל הסמוך הוא בין אם קיימים נקעים או לאו. קיום הנקעים מוביל לפונקציית ה- וכך מקטין את הכוח הדרוש לעיוות הגביש.
פיתוח זה מלמד על ההבדלים בין הכוח המדוד לבין זה התאורטי שהוצגו בסעיף 1.1.
אנרגיה של נקעים ותנאים היווצרם[עריכת קוד מקור | עריכה]
האנרגיה הפוטנציאלית הדרושה ליצירת נקעים[עריכת קוד מקור | עריכה]
כדי למצוא את האנרגיה הדרושה ליצירת נקע נתייחס לגביש תלת־ממדי ובו נקע בורג שנקבע כראשית הצירים. וקטור קו הנקע מקביל לציר ולכן סטיית המיקום גם היא בכיוון זה . נתייחס אל תורת האלסטיות הליניארית עבורה סטיית המיקום רציפה בכל המרחב מלבד בסביבת הנקע.
האנרגיה הפוטנציאלית היא אם כך
a הוא קבוע בעל יחידת אורך שנבחר להיות אורך וקטור בורגרס של הנקע (שאורכו כקבוע הסריג) ו-μ קבוע לאמה. בשיווי משקל סטיית המיקום מקיימת את משוואת לפלס , ולכן הפתרון שיבחר הוא פונקציה אנליטית מרוכבת, בעלת אי רציפות בעת הקפה סביב מרכז הנקע. אי רציפות זו מייצגת את ווקטור בורגרס.
פתרון זה מקיים קפיצה באורך וקטור בורגרס בעת הקפה סביב הראשית כדרוש. הצבה של פתרון זה בביטוי לאנרגיה הפוטנציאלית תניב
האינטגרל מתבצע בין סביבת הנקע - מרחק וקטור בורגרס מהראשית - ובין גבול הגביש R. האיבר מייצג את אנרגיית מרכז הנקע אשר לא ניתנת לחישוב באינטגרל מפאת התבדרות בראשית.
זו, אם כך, האנרגיה הדרושה לשם יצירת נקע בורג יחיד. בהינתן שני נקעים הממוקמים במרחק זה מזה ובעלי ווקטורי בורגרס זהים בגודלם אך הפוכים בכיוונם הפתרון עבור סטיית המיקום יינתן כך
והאנרגיה המתקבלת, על פי חישוב זהה לזה שנעשה עבור נקע יחיד:
מתן אנרגיה, כמו הפעלת כוח או אנרגיית חום, מביא ליצירת נקעים בגביש בהתאם לביטויים הנ"ל.
טמפרטורה קריטית ליצירת נקעים[עריכת קוד מקור | עריכה]
ניתן לראות כי האנרגיה של נקע יחיד מתבדרת עבור גביש גדול מאוד , אך יחד עם זאת קיומם של נקעים מתאפשר מתוך שיקולי אנטרופיה והאנרגיה החופשית של המערכת.
בהנחה כי בריבוע באורך צלע וקבוע סריג יש אתרים למיקום מרכז הנקע, האנטרופיה היא
הצבה של האנטרופיה והאנרגיה של נקע יחיד בביטוי לאנרגיה החופשית של המערכת תניב
בטמפרטורה הקריטית האנרגיה החופשית מתאפסת. מכאן שהטמפרטורה הקריטית היא
בטמפרטורה הגבוהה מטמפרטורה זו ייווצר נקע, והסדר הגבישי יופר כצפוי. על כן כשחומר נחשף לטמפרטורה גבוהה ייווצרו בו נקעים רבים שיובילו לעיוות וכך גם למעבר פאזה.





















![{\displaystyle U(x)={\frac {1}{2}}\mathrm {K} \left[x-a\cdot int(x/a)\right]^{2}-fx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa7a9dbc20ae44a79a9ae719807e3959651f2b56)
![{\displaystyle f_{n}=k\left[x_{n+1}-x_{n}-a\right]+k\left[x_{n-1}-x_{n}+a\right]-{\operatorname {d} \!U \over \operatorname {d} \!x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0510811e16c928048fb3895e99c3a8b227b0f2c9)


![{\displaystyle f_{n}=k\left[x_{n+1}-x_{n}-a\right]+k\left[x_{n-1}-x_{n}+a\right]+f-\mathrm {K} \left[x_{n}-a(n-1)\right];n\leq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11d4d0cf736a1cc129f389c92f9191e7d4d51e62)
![{\displaystyle f_{n}=k\left[x_{n+1}-x_{n}-a\right]+k\left[x_{n-1}-x_{n}+a\right]+f-\mathrm {K} \left[x_{n}-na\right];n>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5162e3581853ddba865b35c1382c2b000aec6e5c)


























