התמרת פורייה
יש לשכתב ערך זה. הסיבה היא: הערך הוא כמעט דף נוסחאות. חסרים הסברים רחבים בהרבה על החשיבות והשימושים.
| ||
| יש לשכתב ערך זה. הסיבה היא: הערך הוא כמעט דף נוסחאות. חסרים הסברים רחבים בהרבה על החשיבות והשימושים. | |

בערך זה |
התמרת פורייה (נקראת גם טרנספורמציית פורייה) היא התמרה אינטגרלית (אנ') המשמשת ככלי מרכזי באנליזה הרמונית. התמרת פורייה היא פירוק של פונקציה לרכיבים מחזוריים (סינוסים וקוסינוסים או לחלופין אקספוננטים מרוכבים) וביצוע אנליזה מתמטית לפונקציה על ידי ניתוח רכיביה. בשל כך ניתן לראות את ההתמרה בתור מיפוי בין מרחב הזמן למרחב התדר. שיטה זו פותחה על ידי ז'אן-בטיסט ז'וזף פורייה וקרויה על שמו.
להתמרות פורייה יש שימוש נרחב מאוד בפיזיקה, בהנדסה ובכל תחום העוסק בפולסים ובגלים, ובפרט באופטיקת גלים ובמכניקת הקוונטים. התמרת פורייה היא אחד הכלים החשובים בהנדסת חשמל ומהווה את הבסיס המדעי לפיתוחים טכנולוגיים בתחומי התקשורת הספרתית, עיבוד אותות ומערכות ליניאריות, עיבוד תמונה וקידוד. כמו כן, התמרת פורייה משמשת ככלי בתחומים רבים נוספים של המתמטיקה, למשל בתור כלי עזר לפתרון של משוואות דיפרנציאליות, או בתורת המספרים האנליטית (למשל נוסחת הסכימה של פואסון). בפיזיקה של מצב מוצק ניתן להשתמש בהתמרת פורייה למעבר מהסריג הישיר (כלומר סריג המתאר את מבנה הגביש במרחב המקום) לסריג הופכי (סריג המתאר את אותו הגביש ב"מרחב הגל").
התמרת פורייה מהווה כלי חשוב בניתוח של צלילים משום שצליל צלול (תו בתדר בודד) הוא למעשה גל קול המתנודד בזמן בתדר מסוים. ההתמרה מאפשרת לנתח צלילים ולבודד את התדרים המרכיבים אותם. באופן כללי יותר, התמרת פורייה מאפשרת לאתר רכיבים מחזוריים בתוך פונקציה, ולכן יש לה שימוש רחב בניתוח אותות ובעיבוד תמונה.
ההתמרה היא הרחבה לטור פורייה – כאשר זמן המחזור של הפונקציה המחזורית בטור פורייה שואף לאינסוף מתקבלת התמרת פורייה.
מוטיבציה – פירוק לפונקציות הרמוניות[עריכת קוד מקור | עריכה]
התמרת פורייה נוצרה מהצורך לפרק כל פונקציה, לצירוף של כמה פונקציות הרמוניות, כאשר פונקציה הרמונית מוגדרת כפונקציה מחזורית בעלת תדירות זוויתית (לפעמים נקראת בקיצור "פונקציה הרמונית" או פשוט "הרמוניה"). הצורה הכללית של פונקציה הרמונית היא:
- .
צירוף ליניארי של כמה פונקציות כאלה נותן ביטוי מהצורה הכללית:
כאשר הוא זמן המחזור של , ו־ היא התמרת פורייה ההפוכה של עבור המחושב כך:
- .
על ידי הכפלת כל מקדם בהרמוניה המתאימה לו וסכימת המכפלות, מקבלים את הפונקציה המקורית כסכום של פונקציות אורתונורמליות (כלומר פונקציות בלתי תלויות ליניארית שהנורמה של כל אחת מהן היא 1). כל אחד מהמקדמים, בתחום הנדסת החשמל ובייצוג של האות (סיגנל) המקורי כתלות בזמן, מייצג עוצמה של תדר במערכת היחידות החדשה שאליה הומר על ידי התמרת פורייה ההפוכה.
כאשר בביטוי האחרון לשם מציאת המקדם, משתמשים בדרך כלל בתוך בערכים של הפונקציה מצורתה הרגילה, כלומר בערכים מתוך הפונקציה המקורית.
– מרחב הפונקציה המותמרת – נקרא מרחב התדירות הזוויתית, או פשוט מרחב התדר. אפשר לראות את המשרעת והפאזה של כרכיבים של אות מחזורי בעל תדירות זוויתית . למרחב המקורי קוראים מרחב הזמן.
משמעות ההתמרה למרחב התדר היא שמקבלים פונקציה מרוכבת שמחזירה עבור כל תדירות את המשרעת והפאזה המתאימות על ידי מספר מרוכב (ערכו המוחלט הוא המשרעת, והזווית שלו היא הפאזה). דבר זה נותן כלי חזק מאוד לניתוח התנהגות של פונקציות מבחינת התדר.
דוגמה לשימוש בהתמרה: בקובצי שמע ניתן לפרק את גל הקול לפונקציות הרמוניות ולהסיר מהקובץ את התדירויות הגבוהות (על ידי מסנן מעביר תדרים נמוכים – low-pass filter) שהאוזן לא שומעת ובכך להקטין את נפח הקובץ באופן משמעותי.
הגדרה פורמלית ראשונה[עריכת קוד מקור | עריכה]
התמרת פורייה של פונקציה מוגדרת כפונקציה כך ש:
(אפשר להגדיר את ההתמרה בעזרת קבועים אחרים, בחירת הקבועים נעשית משיקולי נוחות). ההתמרה מוגדרת רק עבור פונקציות שעבורן אינטגרל כזה מוגדר ולא מתבדר. האינטגרל קיים עבור פונקציות שהן אינטגרביליות בערכן המוחלט לפי לבג, כלומר פונקציות ב-. מכאן ניתן להגדיר את התמרת פורייה בקבוצה שהיא קבוצה צפופה ב-. בשלב הבא מרחיבים את ההתמרה על כל , ומקבלים שהתמרת פורייה מוגדרת על אוסף הפונקציות האינטגרביליות בריבוע לפי לבג – שהוא מרחב הילברט.
התמרת פורייה ההפוכה[עריכת קוד מקור | עריכה]
באופן דומה, אפשר להגדיר את ההתמרה בצורה הבאה, זו ההתמרה של פונקציה שניתנת על ידי
- ,
להתמרה זו קוראים התמרת פורייה ההפוכה.
אפשר לראות שהפעלת התמרת פורייה ההפוכה על התמרת פורייה מחזירה את הפונקציה המקורית.
שכן:
כאשר היא פונקציית דלתא של דיראק.
הגדרה פורמלית שנייה[עריכת קוד מקור | עריכה]
אפשר לרשום כל פונקציה , שהיא פונקציה אינטגרבילית בריבוע לפי לבג (אפשר לרשום זאת בקיצור כך ) כצירוף ליניארי (אינטגרלי) של פונקציות הרמוניות בעלות תדר יחיד באופן הבא:
הפונקציה נתונה על ידי
נקראת "ההצגה של במרחב התדר" בעוד שהפונקציה נקראת "ההצגה של במרחב הזמן".
ניתן להצדיק נוסחה זאת משיקולים של אורתוגונליות במרחב .
טרמינולוגיה:
- ההעתקה המתאימה לכל פונקציה במרחב התדר את הפונקציה המתאימה במרחב הזמן על פי משוואה (1) נקראת "התמרת פורייה ההפוכה".
- ההעתקה המתאימה לכל פונקציה במרחב הזמן את הסט הרציף של המשרעות והפאזות עבור כל תדירות (למעשה, זוהי פונקציה במרחב התדר) על פי משוואה (2) נקראת "התמרת פורייה".
- לעיתים מחליפים בין המונחים הנ"ל בספרים שונים.
סימונים וגורמי נרמול[עריכת קוד מקור | עריכה]
מספר סימונים שונים נהוגים עבור התמרת פורייה וכן ישנן מספר מוסכמות איפה להכניס את גורמי הנרמול בסך .
להלן הגישות הנפוצות בנושא:
- הוספת גורם הנרמול באחד מכיווני ההתמרה.
- הוספת גורם נרמול לפני כל אחת מההתמרות.
- הוספת גורם הנרמול להגדרת המכפלה הפנימית.
גישת הסימונים שהופיעה בהגדרה השנייה היא הגישה הנפוצה בפיזיקה ובהנדסה. היא גם שכיחה במתמטיקה עיונית, אם כי בתחום זה גם גישות סימון אחרות זוכות לתפוצה רחבה.
העיקרון המתמטי שמאחורי התמרת פורייה[עריכת קוד מקור | עריכה]
מרחב הפונקציות האינטגרביליות בריבוע לפי לבג[עריכת קוד מקור | עריכה]
המרחב הוא מרחב הפונקציות האינטגרביליות בריבוע לפי לבג. מרחב זה, בצירוף המכפלה הפנימית
- הוא מרחב הילברט.
אוסף הפונקציות מהווה מערכת אורתונורמלית שלמה, שהיא מעין הכללה של בסיס אורתונורמלי, משמע:
כאשר הפונקציה היא פונקציית דלתא של דיראק. מערכת זו נקראת במתמטיקה "הבסיס ההרמוני" ואילו בפיזיקה קוראים לפונקציות אלה "גלים מישוריים".
במובן זה, המשמעות של הפונקציה המותמרת היא פונקציית ההיטל של הפונקציה המקורית על הבסיס ההרמוני, משמע . והמשמעות של ההתמרה ההפוכה היא פונקציית ההיטל של הפונקציה המקורית על הבסיס ההרמוני המצומד .
התמרת פורייה כאופרטור[עריכת קוד מקור | עריכה]
ניתן לראות את התמרת פורייה כאופרטור . אופרטור זה הוא איזומטריה (כלומר על ושומר מרחקים). ניתן אף להגדיר את התמרת פורייה בגישה זאת, כאשר בהתחלה מגדירים את האופרטור על קבוצה צפופה (מרחב שוורץ למשל) עליה הוא איזומטריה, ומרחיבים מרציפות.
סימונים נוספים[עריכת קוד מקור | עריכה]
לעיתים נהוג לסמן את ההתמרה כפונקציה של הפונקציה המקורית שמחזירה פונקציה אחרת:
או בעזרת אופרטור ה"כובע" על הפונקציה המקורית:
- .
מאחר שסימן ה"כובע" פשוט יותר, הוא יותר מקובל מהשימוש באותיות גדולות או באותיות מסולסלות. כמו כן, את התמרה פורייה ההפוכה נהוג לסמן על ידי כובע הפוך:
- .
לעיתים, כאשר הממשק הגרפי איננו מאפשר ציור "כובע" רחב, שמים את הביטוי המבוקש בסוגריים ואופרטור ה"כובע" (או הכובע ההפוך) מופיע מעליהם בדומה לסימון של חזקה.
התמרת פורייה לאותות בזמן בדיד (DTFT)[עריכת קוד מקור | עריכה]
התמרת פורייה בדידה היא למעשה טור פורייה (כאשר עושים החלפת משתנים בין t ל־θ).
נניח ש־ הוא אות בזמן בדיד, אזי התמרתו נתונה על ידי:
כאשר תנאי מספיק לקיום ההתמרה הוא:
וההתמרה ההופכית נתונה על ידי:
נשים לב ש־ מחזורית במחזור .
הסבר אינטואיטיבי על מחזוריות התדר:
נשים לב כי אות בזמן בדיד הוא בעצם הכפלה של הפונקציה בזמן רציף ב"רכבת הלמים" כאשר רכבת הלמים מוגדרת כך:
T הוא זמן המחזור של הרכבת.
מישור התדר "רגיש" לקפיצות חדות במישור הזמן, כלומר אם יש אי רציפות או שיפוע מאוד גדול בפונקציה זה גורר אחריו תדרים גבוהים (עיקרון זה נובע מהכלל שיובא בהמשך, משמעותו היא שגזירה של אות במרחב משפיעה בצורה ליניארית על מישור התדר, כך שהתדרים הגבוהים מקבלים אמפליטודה גבוהה עם עליית התדר) ולכן בעת מכפלה של הפונקציה המקורית ברכבת הלמים שהיא מחזורית, מישור התדר יתנהג כמו פונקציית ההלמים ויהיה מחזורי.
אפשר גם להסביר את זה מבחינה מתמטית מהעיקרון שמכפלה בזמן שקולה לקונבולוציה בתדר, , והתמרת פורייה של רכבת הלמים שווה לרכבת הלמים (עם זמן מחזור שונה ואמפליטודה שונה), כך שהכפלת האות ברכבת הלמים בזמן יוצרת קונבולוציה של הספקטרום התדירותי של האות עם רכבת הלמים. מהעיקרון שקונבולוציה של כל פונקציה עם הלם משמעותה הזזה של הפונקציה למקומו של ההלם מתקבלת פונקציה מחזורית שכל מחזור בה הוא העתקה של הספקטרום התדירותי המקורי.
מהפיתוח המתמטי הזה עולה שאם דוגמים אות בזמן בדיד, החל מתדר דגימה מסוים (המכונה "תדר נייקוויסט") אפשר לשחזר את האות במלואו ללא איבוד שום מידע שהרי במישור התדר כל הספקטרום התדירותי של האות המקורי נשמר אלא ששוכפל אינסוף פעמים.
נשים לב שנוצרה פה תופעה מעניינת: דגימה בזמן שקולה למחזוריות בתדר. וגם להפך, אם ניקח אות אין סופי שערכו שווה ל־0 החל מזמן מסוים (בערך מוחלט) ונבדוק מהי התמרת פורייה שלו, אחר כך נעשה הרחבה מחזורית של אותו האות כך שכדי לתאר אותו במישור התדר אנו צריכים לעבור לטור פורייה, נגלה שטור פורייה המתקבל הוא בדיוק דגימה של התמרת פורייה המקורית, הרחבה מחזורית בזמן שקולה לדגימה בתדר.
התמרת פורייה לאותות סופיים (או מחזוריים) בזמן בדיד (DFT)[עריכת קוד מקור | עריכה]
עבור המוגדרת על התמרת פורייה הבדידה (DFT) מוגדרת על ידי:
עבור
m=0,1,...,M-1.
ההתמרה במקרה זה היא העתקה ליניארית חח"ע ממרחב ה-M-יות על עצמו.
התמרה זו היא ההתמרה היחידה בה הסכימה היא סופית, דבר שהופך אותה לשימושית מאוד עבור שימושי המחשב.
התמרה זו היא מאוד אינטואיטיבית להבנה, אם מסתכלים עליה מנקודת המבט של אלגברה ליניארית. למעשה, משמעות ההתמרה היא מעבר בין בסיסים ליניאריים.

מקובל לסמן את ההרמוניה הבסיסית
על ידי סימון זה נרשום את מטריצת המעבר בין בסיס הזמן לבסיס התדר:
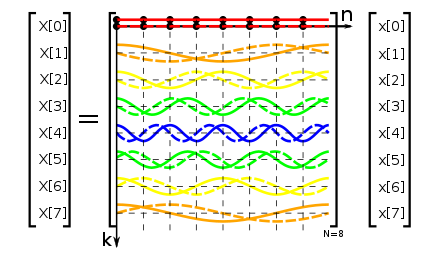
מטריצה זו היא אוניטרית (עד כדי קבוע), הפיכה ומוגדרת חיובית. משמעות הדבר היא שבמעבר למישור התדר אין איבוד מידע (אפשר לחזור למישור הזמן על ידי הכפלה במטריצה ההפוכה) ואין שינוי באנרגיה (אוניטרית, הערכים העצמיים שווים ל-1 בערכם המוחלט).
כאשר עוברים למישור התדר מתקבל וקטור שמשמעותו הוא מהי האמפליטודה הנדרשת עבור כל הרמוניה כדי לבנות את אותו הווקטור כצירוף ליניארי של כל ההרמוניות (וזהו למעשה, ההרכב הספקטרלי של האות). ככל שיהיה יותר דגימות בזמן ,כך מימד המטריצה עולה. משמעות הדבר שהאות מיוצג על ידי יותר תדרים והרזולוציה בתדר עולה.
קשר בין DFT ל-DTFT והעיוות שנוצר ב-DFT
ניתן להסתכל על הווקטור הסופי שעליו מבצעים DFT בזמן כוקטור אינסופי שעליו מבצעים DTFT כאשר כל הדגימות שאינם הווקטור עצמו שוות ל-0. מבט זה מסביר תופעה של עיוות ספקטרלי שנוצרת ב-DFT. ניקח לדוגמה פונקציית קוסינוס פשוטה. התמרת ה-DTFT שלה היא "דלתא" בתדר, כלומר, היא מורכבת רק מתדר אחד.
אמנם אם נעבור לזמן סופי, הדבר שקול להכפלה של הקוסינוס ב"חלון", הקוסינוס מוכפל בפונקציה שמאפסת את כל מה שלא בתחום ההגדרה שלה. כאשר עוברים למישור התדר ההכפלה בחלון הופכת לקונבולוציה עם ההתמרת פורייה של החלון (שהיא למעשה פונקציית sinc) ובמקום "דלתא" יפה בתדר מתקבלת "זליגת אנרגיה" בין תדרים סמוכים. כדי להתגבר על מכשול זה משתמשים בשיטת החלונות (שינוי צורת החלון כך שיוריד את העיוות) או באלגוריתם "WOLA FFT" (ביצוע DFT על ממוצע של מספר חלונות)

תכונות[עריכת קוד מקור | עריכה]
ליניאריות[עריכת קוד מקור | עריכה]
התמרת פורייה והתמרת פורייה ההפוכה הן ליניאריות, כלומר:
על תכונות של העתקות ליניאריות ראו בערך העתקה ליניארית.
משפט פלנשרל וזהות פרסבל[עריכת קוד מקור | עריכה]
משפט פלנשרל קובע ש:
זהות פרסבל היא מקרה פרטי אך שימושי ביותר של משפט פלנשרל.
הפירוש של תכונה זאת היא שימור הנורמה, כלומר היוניטריות של התמרת פורייה.
העיקרון הפיזיקלי של זהות פרסבל הוא שסך האנרגיה של האות במישור הזמן שווה לסך האנרגיה במישור התדר.
קונבולוציה[עריכת קוד מקור | עריכה]
קונבולוציה מוגדרת באופן הבא:
התמרת פורייה מקיימת את הזהויות הבאות בקשר לקונבולוציה:
התכונות האלו של התמרת פורייה הופכות אותה לשימושית מאוד בחישובים מורכבים נומריים, במקום לעשות קונבולוציה (שהיא למעשה סכימה על כל המרחב של הכפלות של פונקציות), נוכל להתמיר את הפונקציות למרחב פורייה ושם לכפול אותן פעם אחת ולהחזיר את התוצאה בהתמרה ההופכית. ולעיתים רבות הדרך השנייה יותר מהירה חישובית.
נשים לב כי קונבולוציה כוללת 3 פעולות[1]: שיקוף הזזה וסכימה (אינטגרציה) והפונקציה המתקבלת היא פונקציה של t כלומר התוצאה תלויה במידת ההזזה.
כמו כן התמרת פורייה כוללת הכפלה ב וסכימה כאשר מתקיימת הנוסחה , כלומר, ההזזה בזמן שקולה להכפלה באקספוננט בתדר. ומכאן נובע משפט הקונבולוציה.
הזזה בזמן[עריכת קוד מקור | עריכה]
משמעות הדבר היא שהזזה במישור הזמן, משמעותה "סיבוב ליניארי" במישור התדר.
כדי להזיז פונקציה בשלמותה, צריך להזיז את התדרים שבה בלי לפגוע בשלמות הפונקציה. כדי לעשות זאת, צריך להזיז את התדרים הנמוכים יותר מהתדרים הגבוהים (בזמן שתדר ω זז מחזור שלם תדר 2ω זז 2 מחזורים).
נגזרת[עריכת קוד מקור | עריכה]
התמרת פורייה מתנהגת בצורה נוחה במיוחד ביחס לפעולת הגזירה.
מאחר שמותר להכניס את סימן הגזירה תחת האינטגרל, קל לראות ש:
ולכן
כלומר, גזירה במרחב הזמן שקולה פשוט לכפל ב־ במרחב התדר.
תכונה שימושית זו נובעת מכך שהפונקציה המעריכית היא פונקציה עצמית של אופרטור הגזירה, שכן
- תכונה זו הופכת את התמרת פורייה למאוד שימושית בעבודה עם מערכות שמאופיינות על ידי משוואה דיפרנציאלית (כגון מערכת LTI).
הכללה למספר ממדים[עריכת קוד מקור | עריכה]
ההכללה לפונקציות ב־ ממדים היא מיידית.
אם פונקציה אינטגרבילית לבג, אזי הפונקציה נקראת "ההצגה של f במרחב וקטור הגל" ונתונה על ידי
וההתמרה ההפוכה מחזירה את הפונקציה המקורית ומוגדרת על ידי
כאשר:
- הוא אינטגרל "נפחי" על כל המרחב (משמע ).
- הוא מכפלה סקלרית ב־.
טבלת התמרות שימושיות[עריכת קוד מקור | עריכה]
הטבלה הבאה מכילה מספר התמרות שימושיות. ו־ מציינות את ההתמרות של ו־ בהתאמה.
| פונקציה | ההתמרה | פירוש | |
|---|---|---|---|
| 1 | ליניאריות | ||
| 2 | הזזה בקבוע | ||
| 3 | כפל בפאזה מרוכבת | ||
| 4 | שינוי סקלה | ||
| 5 | גזירה במרחב הזמן | ||
| 6 | גזירה במרחב התדר | ||
| 7 | קונבולוציה | ||
| 8 | אופרטור הצמוד | ||
| 9 | מכפלה | ||
| 10 | דלתא של דיראק | ||
| 11 | - | ||
| 12 | - | ||
| 13 | - | ||
| 14 | קוסינוס | ||
| 15 | סינוס | ||
| 16 | גאוסיאן | ||
| 17 | התמרת פונקציית המלבן לפונקציית sinc | ||
| 18 | - | ||
| 19 | - | ||
| 20 | גל מרובע |
שימושים[עריכת קוד מקור | עריכה]
- מתמטיקה
- פתרון משוואות דיפרנציאליות (בעיקר חלקיות)
- אנליזה הרמונית
- אנליזה פונקציונלית
- פיזיקה
- גלים
- פתרון משוואת הגלים
- פתרון משוואת החום
- קרינה אלקטרומגנטית
- מכניקת הקוונטים
- פתרון משוואת שרדינגר
- מדעי המחשב
- הנדסה
ראו גם[עריכת קוד מקור | עריכה]
- טור פורייה
- תורת שטורם-ליוביל
- שדה המספרים המרוכבים
- חשבון אינפיניטסימלי
- אלגברה ליניארית
- מרחבי מכפלה פנימית ובפרט מרחב הילברט
- אורתוגונליות
- משוואות דיפרנציאליות
- אופרטור הרמיטי
- התמרת פורייה קוונטית
- התמרת לפלס
- התמרת האף
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- מחשבון להתמרה פורייה ישירה והפוכה
- התמרת פורייה – טרנס טאו
- ארז גרטי, פורייה: עושים גלים, באתר של מכון דוידסון לחינוך מדעי, 5 נובמבר 2011
- התמרת פורייה, באתר MathWorld (באנגלית)
- סרטון הסברה על מישור התדר
- מבוא רעיוני להתמרת פורייה מתוך הבלוג "רשימות בפיזיקה עיונית"
 building the Fourier transform, סרטון בערוץ "Michael Penn", באתר יוטיוב (אורך: 23:12)
building the Fourier transform, סרטון בערוץ "Michael Penn", באתר יוטיוב (אורך: 23:12)- התמרת פורייה, באתר אנציקלופדיה בריטניקה (באנגלית)












































![{\displaystyle \ x[n]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98ced457fbdfb2c87a5cb5375b403a1c1c8212f6)
![{\displaystyle \ X^{f}(\theta )=\sum _{n=-\infty }^{\infty }x[n]e^{-i\theta n}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5258face8985e8c33856049f34f226e9006a2a67)
![{\displaystyle \ \sum _{n=-\infty }^{\infty }\left|x[n]\right|<\infty }](https://wikimedia.org/api/rest_v1/media/math/render/svg/116e0b9e900cfe06281e346cb7e18c343ca2d65f)
![{\displaystyle \ x[n]={\frac {1}{2\pi }}\int _{-\pi }^{\pi }X^{f}(\theta )e^{i\theta n}d\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7b3c8d7e2afb0bbf472cdc2ecb8dbdf74ab2636)






![{\displaystyle \ X^{f}(m)={\frac {1}{M}}\sum _{n=0}^{M-1}x[n]e^{-2i{\pi }mn/M}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93c53be203a7d6609af1f1f51c1fdf3dac13a56e)

































































