הקס (משחק)
מתוך ויקיפדיה, האנציקלופדיה החופשית
| הקס | |
|---|---|
 תכולת המשחק |
|
| יוצר | פייט היין וג'ון נאש |
| מס' שחקנים | 2 |
| גילאים | מעל 4 |
| זמן המשחק | כ-15 דקות (על לוח 11X11) |
| מיומנות | אסטרטגיה וטקטיקה |
הקס הוא שמו של משחק לוח המתנהל על לוח מרוצף משושים. המשחק הומצא באמצע המאה ה-20, ומשום פשטותו רכש פופולריות רבה במהירות. למרות החוקים הפשוטים, המשחק מורכב מאוד ומכיל אפשרויות רבות. אנשי תורת המשחקים הוכיחו שלשחקן הראשון ישנה אסטרטגיה המבטיחה לו ניצחון במשחק, אולם אסטרטגיה זאת עדיין לא נמצאה.
תוכן עניינים |
[עריכה] חוקים
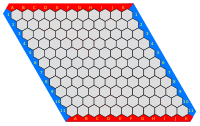
המשחק מתנהל על לוח המרוצף משושים, כמצויר באיור, שגודלם לרוב 11x11 או 13x13. בכל תור, אחד השחקנים צובע משבצת ריקה באדום או בכחול, לסירוגין (מקובל שצבעו של השחקן הראשון - אדום). מטרתו של כל שחקן היא לקשר את צידי הלוח המסומנים בצבע שלו, בשרשרת רצופה של משושים בצבע זה. השחקן הראשון המצליח במשימה, ומונע בכך מן השחקן השני להשלים שרשרת משלו, מנצח.
[עריכה] היסטוריה
את המשחק המציאו, באופן בלתי תלוי, המשורר והמתמטיקאי הדני פייט היין ב-1942, והמתמטיקאי איש תורת המשחקים ג'ון נאש, ב- 1942. נאש הצליח גם להוכיח שלשחקן הראשון יש אסטרטגיית ניצחון במשחק (למרות שהאסטרטגיה כזאת לא התגלתה עד היום).
בשנת 1952 החלה חברת המשחקים Parker Brothers לשווק את המשחק תחת השם "הקס", הגזור מן המלה האנגלית Hexagon - משושה. היום קיימות למשחק גם גרסאות מחשב ורשת.
[עריכה] לוחות שונים לאותו משחק
מבחינה מהותית תלוי המשחק רק בקשרים שבין משבצות סמוכות, ולא בגודלן או בצורתן. הגרסה המוזכרת כאן, שבה הלוח משושה, מיוחסת להיין. אצל נאש היה הלוח משובץ משבצות ריבועיות, כאשר זוג משבצות מקושרות אם הן חולקות צלע משותפת, או אם אחת מהן נמצאת משמאל ומעל השנייה. באותה מידה ניתן לשחק את המשחק על גרף, שבו נקודות מציינות את המשבצות, והשחקנים מניחים דיסקיות מעל הנקודות, כמו בתמונה השלישית.
 המשחק הקס, בלוח 5x5, מצב מנצח לשחקן האדום |
 הקס בגרסת המשבצות של ג'ון נאש; המצב באיור זהה למצב באיור הראשון |
[עריכה] גניבה של אסטרטגיה
אחת הפנינים של תורת המשחקים הקומבינטורית היא ההוכחה שבמשחק הקס לשחקן הראשון יש אסטרטגיה המבטיחה לו ניצחון. כלומר, במידה וישחק משחק מושלם, הוא בהכרח ינצח. ההוכחה, שמקורה בנאש, משתמשת בשיטה הנקראת גניבה של אסטרטגיה, שניתן להשתמש בה במגוון רחב של משחקים נוספים, כגון בווריאציות שונות של איקס עיגול.
על-פי משפט צרמלו, בכל משחק או שיש לשחקן הראשון אסטרטגיה המבטיחה לו ניצחון (כלומר יש דרך שבה הוא יכול לנצח לא משנה מה עושה השחקן השני), או שיש לשחקן השני אסטרטגיה כזאת, או ששני השחקנים יכולים להבטיח לעצמם תיקו. בהקס לא תיתכן תוצאה של תיקו, כפי שנוכיח בפסקה הבאה, ולכן נותר להוכיח שלשחקן השני אין אסטרטגיה המבטיחה לו ניצחון. נניח בשלילה שיש לו אחת כזאת, אזי השחקן הראשון יכול לסמן בתור הראשון משושה כלשהו, ואחר כך להשתמש באסטרטגיה של השחקן השני, בשביל להבטיח לעצמו ניצחון. באם, תוך כדי המשחק, האסטרטגיה אומרת לו לסמן את המשושה שהוא סימן במהלך הראשון, אזי הוא מסמן משושה אחר. מכאן מקבלים את התוצאה המפתיעה שגם השחקן הראשון וגם השני יכולים לכפות ניצחון וזו סתירה, מכאן שאין לשחקן השני אסטרטגיה המבטיחה לו ניצחון.
[עריכה] אין תיקו בהקס
הנחנו מקודם שאין תיקו במשחק, וכעת נוכיח שאכן כאשר כל המשבצות בהקס מסומנות אזי זהו מצב מנצח לשחקן הראשון או לשחקן השני. באופן אינטואיטיבי זה נראה מובן מאליו שכן הדרך היחידה בשביל השחקן הכחול למנוע גשר של משושים אדומים משני הקצוות האדומים היא ליצור גשר של משושים כחולים משני הצדדים המסומנים בכחול. על מנת להוכיח זאת, נדמיין טיול שמתבצע על הצלעות של המשושים בלוח המצויר באיור הראשון. מתחילים בפינה העליונה והכלל של הטיול הוא שבכל מהלך ממשיכים לצלע שנמצאת בין אזור אדום לאזור כחול. לא קשה לראות שהטיול יכול להסתיים רק באחת מהפינות האחרות של הלוח, ואם הוא מסתיים בפינה השמאלית אזי יש ניצחון לכחול, ואם הוא מסתיים בפינה הימנית אזי יש ניצחון לאדום.
