גרף מישורי

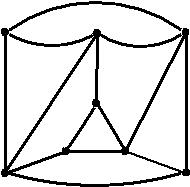
מתוך ויקיפדיה, האנציקלופדיה החופשית

ייצוג גרפי של גרף מישורי

בתורת הגרפים, גרף מישורי הוא גרף שניתן לצייר במישור מבלי שהקשתות יחתכו זו את זו (חוץ מאשר בצומתי הגרף). לגרפים כאלה יש חשיבות מיוחדת באלגוריתמים הקשורים בראייה ממוחשבת וביישומים של תורת הגרפים בתעשייה, למשל לתכנון מעגלים חשמליים.

[עריכה] הגדרות פורמליות

גרף מישורי הוא גרף הניתן לשיכון במישור. שיכון של גרף במישור הוא מודל גאומטרי שלו, שבו הצמתים הם נקודות במישור והקשתות הן עקומות שלא חותכות את עצמן או אף עקומה אחרת (חוץ מאשר בקודקודי הגרף). קל לראות שכל גרף ניתן לשיכון במרחב האוקלידי התלת-ממדי $\mathbb{R}^3$ ; נוכל, למשל, לשכן את צומתי הגרף על ציר אחד ולכל קשת נקצה מישור משלה.

פאות של גרף משוכן במישור הן רכיבי הקשירות שנקבל במישור אם נסיר את הצלעות (האזורים שנתחמים על ידי הקשתות). האזור שמחוץ לצורה שיוצר הגרף הינו הפאה היחידה שאינה חסומה.

מקובל לסמן את מספר הצמתים של הגרף באות v, את מספר הקשתות ב- e, ואת מספר הפאות באות f.

[עריכה] נוסחת אוילר

ערך מורחב – נוסחת אוילר (תורת הגרפים)

גרף מישורי קשיר מקיים:

$\ f = e - v+ 2$

הוכחה: באינדוקציה על מספר הפאות, אם f = 1 אז אין בגרף מעגלים, לכן (הגרף קשיר) מדובר בעץ ומתקיים e = v - 1. אם f > 1 יש בגרף מעגל. כל קשת במעגל מהווה שפה לשתי פיאות בדיוק ואם נסיר אחת נקטין את מספר הקשתות והפאות באחת.

עבור גרף מישורי עם k רכיבי קשירות נכליל:

$\ f = e - v + k + 1$

הוכחה: (שימו לב שהפאה החיצונית משותפת לכל רכיבי הקשירות) $f=\sum_{i=1}^{k}(e_i-v_i+2) - (k-1) = e-v+k+1$

באופן כללי יותר, אם במקום לצייר את הגרף במישור מציירים אותו על-פני משטח קומפקטי כלשהו, הצירוף $\ f-e+v$ הוא קבוע, השווה למאפיין אוילר של המשטח. לנוסחה זו יש גם פירוש הומולוגי.

[עריכה] תנאים למישוריות

להלן כמה תנאים הכרחיים (ולא מספיקים) להיות גרף מישורי:

משפט: בגרף מישורי $e\leq 3v -6$

הוכחה: כל קשת גובלת בשתי פאות לכל היותר ופאה נתחמת על ידי שלוש קשתות לפחות, כלומר $f\leq \frac{2e}{3}$ ויחד עם נוסחת אוילר יתקבל: $\ e-v+2\leq \frac{2e}{3}$ .

מסקנה: הגרף השלם בן חמישה קודקודים $\ K_5$ אינו מישורי ( $\ e=10 \ v=5$ ).
מסקנה נוספת: בגרף מישורי $\delta(G)\leq 5$ כאשר $\ \delta(G)$ הינו הדרגה המינימלית של קודקוד בגרף.

הוכחה: אחרת $\ e=\frac{1}{2}\cdot \sum_{x\in V}^{}d(x) \geq \frac{6\cdot v}{2}=3\cdot v$ .

משפט: בגרף מישורי $\ e\leq \frac{g}{g-2}\cdot(v-2)$ כאשר g הוא מותן הגרף.

הוכחה: זהו חידוד של המשפט הקודם, כאשר הפעם כל פאה נתחמת על ידי g קשתות לפחות.

מסקנה: הגרף הדו צדדי השלם $\ K_{3,3}$ אינו מישורי (כאן המותן שווה ל-4).

[עריכה] משפט קורטובסקי (Kuratowsky)

הגרף

K 5

הגרף

K 3,3

הגרף השלם $\ K_5$ והגרף הדו-צדדי השלם $\ K_{3,3}$ אינם מישוריים, ואם כך גם החלוקות שלהם אינן מישוריות. מתברר שזהו ההסבר היחיד לאי-מישוריות: כל גרף שאין לו תת-גרף שהוא חלוקה של אחד משני הגרפים הבעייתיים, הוא גרף מישורי.

זוהי תוצאה אופיינית בתחום הנקרא Extermal graph theory, שבו 'מסבירים' מדוע גרף נכשל מלקיים תכונה מסוימת בכך שהוא מכיל אחד מבין מספר קטן של תת-גרפים בעייתיים. לדוגמה, אפשר לומר שגרף הוא k-מישורי אם אפשר לשכן אותו במישור, באופן שיש לכל היותר k חיתוכים בין קשתות (גרף 0-מישורי הוא גרף מישורי במובן שהוגדר לעיל). אז לכל k קיימת קבוצה סופית של גרפים 'אסורים', כך שכל גרף שאינו k-מישורי מכיל תת-גרף אסור.

[עריכה] גרפים מישוריים ומפות

כשקרטוגרף מצייר מפה מדינית, הוא משתדל לצבוע מדינות שכנות בצבעים שונים, כדי להקל על ההבחנה ביניהן. הדרך הטבעית לחקור מצבים כאלה בתורת הגרפים היא להגדיר את הגרף הדואלי למפה, שבו הצמתים הם המדינות, וזוג צמתים מחוברים בקשת רק כאשר המדינות המתאימות שכנות זו לזו. מכיוון שהמפה המקורית היא מישורית (או כדורית, אם מדובר במפה כלל-עולמית), הגרף המתקבל הוא גרף מישורי.

המשימה של הגאוגרף היא לצבוע את צומתי הגרף, באופן שזוג צמתים מחוברים ייצבעו בצבעים שונים. משפט ארבעת הצבעים מבטיח שתמיד ניתן לעשות זאת בארבעה צבעים או פחות. בלשון אחרת, המשפט מבטיח שלכל גרף מישורי יש 4-צביעה.

מקור: http://he.wikipedia.org/wiki/%D7%92%D7%A8%D7%A3_%D7%9E%D7%99%D7%A9%D7%95%D7%A8%D7%99