גרף קשיר
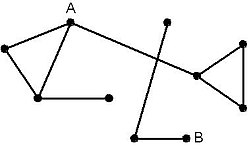
בתורת הגרפים, גרף בלתי מכוון נקרא קשיר אם קיים מסלול בין כל שני צמתים בגרף. גרף מכוון נקרא קשיר היטב (או קשיר חזק) אם קיים בו מסלול מכוון מכל צומת לכל צומת אחר.
פורמלית, גרף ייקרא קשיר אם לכל זוג צמתים ו- ב- קיימת סדרה של קשתות ב- כך שאם לכל אז:
א. . דהיינו, המסלול מתחיל בצומת .
ב. . דהיינו, המסלול מסתיים בצומת .
ג. לכל מתקיים . דהיינו, סדרת הקשתות מהווה מסלול בגרף.

יש לשים לב כי ההגדרה הנ"ל משתנה קלות כאשר מדובר בגרפים לא מכוונים או בגרפים מכוונים. במקרה הראשון, קשת היא קבוצה בת שני צמתים, ואילו במקרה השני, קשת היא זוג סדור של שני צמתים.
במתמטיקה באופן כללי, ובעיקר בטופולוגיה, קשירות של קבוצה מציינת שכל הקבוצה היא "בחתיכה אחת". בתורת הגרפים קשירות מתבטאת בכך שכל צומתי הגרף מחוברים יחד, במובן זה שניתן להגיע מכל צומת לכל צומת אחר. קשירות היא דרישה בסיסית מגרפים, על מנת שיקיימו תכונות נוספות. למשל, כדי שיהיה בגרף מסלול אוילרי, הכרחי שהוא יהיה קשיר (עד כדי צמתים שאינם מחוברים כלל לקשתות). קשירות היא גם דרישה בסיסית מעץ.
רכיבי קשירות[עריכת קוד מקור | עריכה]
רכיב קשירות של גרף הוא תת-גרף קשיר מקסימלי, כלומר, קבוצת קודקודים שיש מסלול בין כל שני קודקודים שלה, והכוללת עם כל קודקוד גם את השכנים שלו; יחד עם הקשתות המחברות את הקודקודים האלה. כל גרף מתפרק באופן יחיד לרכיבי קשירות.
דרך נוספת להגדיר רכיבי קשירות היא: נתבונן ביחס על הקודקודים בגרף "יש מסלול ביניהם" זהו יחס שקילות (כאשר בין קודקוד לעצמו יש תמיד את המסלול הריק) אז רכיב קשירות הוא מחלקת שקילות.
רכיב קשיר היטב[עריכת קוד מקור | עריכה]

גרף מכוון נקרא קשיר היטב (או קשיר בחוזקה) אם קיים מסלול מכל צומת שבו אל כל צומת אחר. עבור גרף מכוון כללי, ניתן תמיד לפרק את הגרף לרכיבים קשירים היטב - תתי-גרפים מקסימליים של הגרף המקורי (גם: רק"ח - רכיבי קשירות חזקה), שכל אחד מהם הוא גרף קשיר היטב בפני עצמו. פירוק זה מהווה חלוקה של הגרף למחלקות זרות - שני רכיבים שונים לא יכולים להכיל צומת משותף.
גרף מכוון חסר מעגלים (גמ"ל - DAG): גרף בו כל צומת (וקשתותיו היוצאות) מהווה רק"ח יחיד, ויש קשת מכוונת בין שני צמתים אם ורק אם יש קשת בין הרכיבים בגרף המקורי.
אלגוריתמים רבים בתורת הגרפים מניחים שהגרף עליו הם פועלים קשיר היטב, ועל כן מפעילים אותם על כל רכיב קשיר היטב בנפרד.
גרף מכוון בו עבור כל שני קדקודים קיים מסלול מ- ל- או מ- ל- נקרא קשיר למחצה.
גרף מכוון הנעשה קשיר לאחר הסרת הכיווניות נקרא קשיר חלש.
אלגוריתם למציאת רכיבים קשירים היטב[עריכת קוד מקור | עריכה]
אלגוריתם Kosaraju (אנ') הוא דרך פשוטה יחסית למציאת הרכיבים הקשירים היטב בגרף שזמן ריצתו ליניארי בגודל הגרף. האלגוריתם מתבסס על שימוש כפול באלגוריתם חיפוש לעומק - פעם אחת על הגרף עצמו, ופעם על הגרף ה"משוחלף" המתקבל מהיפוך כל כיווני הקשתות.
תיאור האלגוריתם:
- ראשית מפעילים את אלגוריתם חיפוש לעומק על , ועבור כל צומת זוכרים את זמן היציאה ממנו.
- כעת מחשבים את . הדבר ניתן לביצוע בזמן ליניארי.
- כעת מפעילים את אלגוריתם חיפוש לעומק שנית, הפעם על . מתחילים את ריצת האלגוריתם מהצומת בעל זמן היציאה הגבוה ביותר מבין אלו שחושבו בשלב 1, וכאשר האלגוריתם מסיים את הסריקה שהחלה מהצומת הזה ועליו לבחור צומת חדש, בוחרים את הצומת בעל זמן היציאה הגבוה ביותר מבין אלו שנשארו, וכן הלאה.
- תוצאת האלגוריתם שהופעל בשלב 3 היא יער. כל אחד מהעצים שביער הוא אחד מהרכיבים הקשירים היטב שבגרף, וכולם מופיעים בו. מוציאים אותם כפלט, בהתאם למבוקש (תוצאות החיפוש לעומק בלבד אינן מספיקות, שכן הוא בוצע על הגרף המשוחלף).
הסיבה לכך שמובטח שהאלגוריתם יעבוד כהלכה היא זו: אם הם שני רכיבים קשירים היטב בגרף כך שיש קשת מ- אל , אז מובטח כי זמן היציאה שחושב בשלב 1 עבור צומתי גדול מזה שחושב עבור צומתי (לא קיימת קשת מ- אל , שכן אז היו שני הרכיבים הללו מתמזגים לרכיב אחד).
על כן, בגרף המשוחלף , לא קיימת קשת מ- אל (כי הקשתות הפכו את כיוונן). מכיוון שאלגוריתם החיפוש לעומק בשלב 3 מתחיל את ריצתו מהרכיב שמכיל את הצומת בעל זמן היציאה הגדול ביותר שהוא נמצא בהכרח ב- , ולכן מרכיב זה לא ניתן להגיע לרכיבים אחרים, והאלגוריתם יחשב אותו בלבד. לאחר שהאלגוריתם פעל על רכיב זה צמתיו מסומנים כך שהאלגוריתם לא ייכנס אליהם שוב, ולכן מובטח כי גם המשך פעולת האלגוריתם תחזיר את התוצאה הנכונה.
קשירות מרובה[עריכת קוד מקור | עריכה]
גרף נקרא k-קשיר (בקודקודים) אם הוא נותר קשיר לאחר הסרת פחות מ-k קודקודים, ו-k-קשיר-קשתות אם הוא נותר קשיר לאחר הסרת פחות מ-k-קשתות. גרף "1-קשיר-קשתות" אינו אלא גרף קשיר. משפט מנגר קובע כי גרף הוא k-קשיר אם ורק אם בין כל שני קודקודים בגרף קיימים k מסלולים זרים בקודקודים והוא k-קשיר-קשתות אם ורק אם בין כל שני קודקודים בגרף קיימים k מסלולים זרים בקשתות.
| נושאים בתורת הגרפים | ||
|---|---|---|
| הגדרות | צומת • קשת • דרגה • מסלול • מרחק | |
| מבנים | גרף • גרף ממושקל • מעגל • גרף מקרי • היפרגרף • מולטיגרף • עץ • קומפלקס | |
| בניות וטיפוסים | גרף משלים • גרף קיילי • גרף שלם • גרף תחרות • עץ פורש • רשת זרימה • שידוך | |
| תכונות | גרף n-צביע • גרף דו-צדדי • גרף מישורי • גרף מרחיב • גרף רגולרי • גרף קשיר • עץ בינומי • עץ פורש מינימלי | |




















