חלקיק בפוטנציאל מרכזי

במכניקת הקוונטים, חלקיק בפוטנציאל מרכזי הוא מערכת קוונטית עם פוטנציאל שתלוי רק במרחק בין החלקיק ונקודת המוקד של הכוח המרכזי. דוגמה אחת למערכת כזו היא האלקטרון באטום המימן. הפוטנציאל בו מצוי האלקטרון תלוי רק במרחקו מהפרוטון שבגרעין אטום המימן. פוטנציאל זה ניתן לגזירה מחוק קולון.

במקרה הכללי, הדינמיקה של חלקיק בפוטנציאל ספרי סימטרי נשלטת על ידי המילטוניאן מהצורה:

$${\hat {H}}={\frac {{\hat {p}}^{2}}{2m_{0}}}+V(r)$$

כאשר $m_{0}$ היא מסת החלקיק, ${\hat {p}}$ הוא אופרטור התנע, והפוטנציאל $V(r)$ תלוי רק ב-$r$, כלומר באורך הרדיוס וקטור. המצבים הקוונטיים האפשריים של החלקיק ניתנים לחישוב דרך משוואת שרדינגר עבור ההמילטוניאן הנתון, ממנה ניתן למצוא את הערכים העצמיים של הגדלים הפיזיקליים הרלוונטיים כמו גם את המצבים העצמיים המתאימים להם, שהם פונקציות גל.

כדי לתאר את המערכות הספריות הסימטריות הללו, טבעי להשתמש בקואורדינטות כדוריות $r$, $\theta$ ו-$\phi$. לאחר שכותבים את משוואת שרדינגר בקואורדינטות אלו, משוואת שרדינגר הבלתי תלויה בזמן בעבור מערכת כזו היא פרידה. פירוש הדבר שפתרון החלק הזוויתי של המשוואה ניתן לקביעה באופן בלתי תלוי בחלק הרדיאלי. זה מותיר משוואה דיפרנציאלית רגילה במונחי הרדיוס בלבד, אשר ממנה נגזרים המצבים העצמיים בעבור הפוטנציאל הנתון.

מבנה הפונקציות העצמיות

המצבים העצמיים של המערכת הם מהצורה:

$$\psi (r,\theta ,\phi )=R(r)\Theta (\theta )\Phi (\phi )$$

שבה הזוויות θ,φ הן הזווית הפולרית והאזימוטלית בהתאמה. שני החלקים הזוויתיים של פונקציות הגל העצמיות ψ נכתבים לעיתים כגורם מנורמל יחיד הנקרא הרמוניה ספרית, כך שהפונקציות העצמיות מקבלות את הצורה:

$$\psi (r,\theta ,\phi )=R(r)Y_{\ell m}(\theta ,\phi ).$$

המשוואה הדיפרנציאלית שמתארת את הפונקציה $R(r)$ מכונה המשוואה הרדיאלית.

גזירת המשוואה הרדיאלית

אופרטור האנרגיה הקינטית בקואורדינטות כדוריות הוא:

$${\frac {{\hat {p}}^{2}}{2m_{0}}}=-{\frac {\hbar ^{2}}{2m_{0}}}\nabla ^{2}=-{\frac {\hbar ^{2}}{2m_{0}\,r^{2}}}\left[{\frac {\partial }{\partial r}}\left(r^{2}{\frac {\partial }{\partial r}}\right)-{\hat {L}}^{2}\right].$$

ההרמוניות הספריות מקיימות:

$${\hat {L}}^{2}Y_{\ell m}(\theta ,\phi )\equiv \left\{-{\frac {1}{\sin ^{2}\theta }}\left[\sin \theta {\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial }{\partial \theta }}\right)+{\frac {\partial ^{2}}{\partial \phi ^{2}}}\right]\right\}Y_{\ell m}(\theta ,\phi )=\ell (\ell +1)Y_{\ell m}(\theta ,\phi ).$$

ואם נציב זאת במשוואת שרדינגר נקבל בעיית ערך עצמי חד-ממדית,

$${\frac {1}{r^{2}}}{\frac {d}{dr}}\left(r^{2}{\frac {dR}{dr}}\right)-{\frac {\ell (\ell +1)}{r^{2}}}R+{\frac {2m_{0}}{\hbar ^{2}}}\left[E-V(r)\right]R=0.$$

את משוואה זו ניתן להפוך למשוואת שרדינגר חד-ממדית שקולה בעזרת ההצבה $R(r)=u(r)/r$, כאשר $u(r)$ מקיימת:

$${d^{2}u \over dr^{2}}+{\frac {2m_{0}}{\hbar ^{2}}}\left[E-V_{\mathrm {eff} }(r)\right]u=0$$

וזוהי בדיוק משוואת שרדינגר החד-ממדית עם פוטנציאל אפקטיבי שניתן על ידי

$$V_{\mathrm {eff} }(r)=V(r)+{\hbar ^{2}\ell (\ell +1) \over 2m_{0}r^{2}},$$

כאשר הקואורדינטה הרדיאלית r נעה בין 0 ל-$\infty$.

דיון סמי-קלאסי בפונקציית הגל של חלקיק בפוטנציאל מרכזי

במכניקה קלאסית, מסלולו של חלקיק בפוטנציאל מרכזי נקבע באופן חד-חד ערכי על ידי התנע הזוויתי שלו L והאנרגיה הכוללת שלו E, שמהווים שמורות תנועה. אף על פי שבמכניקת הקוונטים אין מיקום ותנע מוגדרים לחלקיק וניתן לדבר רק על פונקציית הגל שלו (שמייצגת את הסיכוי למצוא את החלקיק במיקום כלשהו), אינטואיציות "קלאסיות" רלוונטיות במידת מה גם עבור המקרה הקוונטי. מכיוון שבמכניקת הקוונטים החלקיק אינו נקודתי אלא "מרוח" במרחב, אפשר לתאר מצבים עצמיים של המערכת רק דרך שפה של אופרטורים; משוואת שרדינגר לחלק הרדיאלי כפי שתוארה לעיל, מתייחסת לפוטנציאל האפקטיבי דרך האופרטור ${\hat {L}}^{2}$ (ריבוע התנע הזוויתי). החלק הזה מוקדש לתיאור מאפיינים "איכותיים" כלליים של המצבים העצמיים של חלקיק קשור בפוטנציאל מרכזי. אף על פי שהדיון כאן לא מתייחס לפוטנציאל ספציפי, הוא תקף למרבית סוגי הפוטנציאלים (בפרט לאלקטרון באטום המימן).

תיאור איכותי של החלק הזוויתי

מצבים עצמיים של האלקטרון באטום המימן ברמות אנרגיה שונות. ההסתברות למצוא את האלקטרון נתונה על ידי הצבע, כפי שמוראה במפתח הקריאה בצד ימין למעלה. ניתן לראות שמצבים ללא תנע זוויתי הם בעלי סימטריה כדורית.

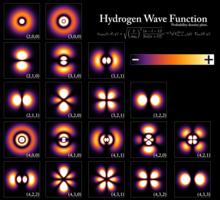
הבדל מהותי אחד בין הבעיה הדו-גופית הקלאסית להתנהגותו של חלקיק קוונטי הוא שבבעיה הקלאסית לא ייתכנו מצבים קשורים ללא תנע זוויתי (למעט אלו המתארים נפילה של החלקיק ישירות אל מרכז הכוח). לעומת זאת, חלקיק קוונטי מרוח בכל המרחב שמסביב למרכז הכוח ולכן כל עוד פונקציית הגל שלו היא בעלת סימטריה כדורית (כלומר כאשר החלק הזוויתי שלה הוא טריוויאלי) אין שום סיבה שהיא תתאר מישור תנועה מוגדר או באופן שקול תתאים לערך שונה מאפס של אופרטור ההיטל של התנע הזוויתי ${\hat {L}}_{z}$ על ציר מסוים; מכיוון שבמקרה זה ערכי התצפית של אופרטור ההיטל של התנע הזוויתי מתאפסים ביחס לכל ציר, ניתן לקבוע שבמצבים עצמיים בעלי סימטריה כדורית התנע הזוויתי מתאפס. תפקיד התנע הזוויתי בגרסה הקוונטית של בעיית הכוח המרכזי הוא "לשבור" את הסימטריה הכדורית של פונקציית הגל של החלקיק הקשור.

מבחינה מתמטית, עבור מצב קשור נתון של חלקיק בפוטנציאל מרכזי, ככל שהמספר הקוונטי הזוויתי $l$ גדול יותר, ההרמוניה הספרית המתאימה מתוארת על ידי פולינום לז'נדר נלווה $P_{l}^{m}(\mathbb {cos\theta } )$ ממעלה גבוהה יותר ב-$\mathbb {cos\theta }$, ולפיכך מייצג תצורה מרחבית מורכבת יותר בעלת קווי צומת מורכבים יותר. המספר הקוונטי האזימוטלי $m$, שמייצג את ההיטל של התנע הזוויתי על ציר z, ניתן לתיאור (בשפה השאולה מהפיזיקה הקלאסית) כ"תדירות המרחבית" של התנדנדות פונקציית הגל (מספר גל) לאורך מעגל במישור שניצב לציר זה. במילים אחרות, החלק הזוויתי שתלוי ב-$\theta$ בלבד (ותואם למספר הקוונטי הזוויתי) הוא קבוע על פני חרוטים בעל זווית ראש $\theta$ בעוד שהחלק הזוויתי שתלוי ב-$\phi$ בלבד קבוע לאורך קרן בזווית $\phi$ במישור XY.

תיאור איכותי של החלק הרדיאלי

במכניקה קלאסית, מאחר שהתנע הזוויתי L מהווה שמורת תנועה עבור פוטנציאלים מרכזיים, בפתרון הבעיה הדו-גופית נהוג לתאר את התנהגות המערכת בעזרת גודל הנקרא "פוטנציאל אפקטיבי"

$$V_{\mathrm {eff} }(r)=V(r)+{\frac {L^{2}}{2mr^{2}}},$$

, אשר כולל בתוכו הן את השפעת האפקט הצנטריפוגלי של התנע הזוויתי והן השפעת הכוח המרכזי ומאפשר לצמצם את הבעיה התלת-ממדית לבעיה חד-ממדית. האנרגיה הכוללת E מטילה הגבלות על תחום הערכים האפשריים של r (מרחק החלקיק ממרכז הכוח המרכזי). בניתוח הקלאסי של הבעיה הדו-גופית ניתן להראות שאם משנים את התנע הזוויתי L בעוד ששומרים על אנרגיה כוללת קבועה E, אז הקטנת התנע הזוויתי מגדילה את מנעד הערכים של r בו החלקיק יכול להימצא, כלומר מגדילה את המרחק בין הפריהליון לאפהליון.

בגרסה הקוונטית של הבעיה, כאשר פותרים את משוואת שרדינגר לחלק הרדיאלי $R(r)$ של פונקציית הגל, מגלים שהחלק הרדיאלי תלוי גם בתנע הזוויתי L של החלקיק, בנוסף על האנרגיה הכוללת E. להשפעת הקטנת התנע הזוויתי במקרה הקוונטי יש קווי דמיון עם המקרה הקלאסי – מנעד הערכים של r בהם הסיכוי למצוא את החלקיק גבוה (כלומר שצפיפות ההסתברות $|R(r)|^{2}$ אינה זניחה) הולך וגדל. ניתן למתוח את האנלוגיה הקלאסית אף יותר - בבעיה הדו-גופית הקלאסית הקטנת התנע הזוויתי מגדילה את האקסנצטריות של מסלולו האליפטי של החלקיק, כך שבמרבית זמן המחזור של התנועה החלקיק יהיה מצוי במרחקים גדולים יותר - ולכן הגיוני לצפות שבגרסה הקוונטית שלה תוחלת מרחק החלקיק ממרכז הכוח תגדל עם הקטנת L. למשל, עבור אטום המימן, תוחלת מרחק האלקטרון מהגרעין, שמוגדרת להיות:

$<r>=\int _{0}^{\infty }r\cdot (|R(r)|^{2}4\pi r^{2})dr$

מקיימת את הקשר:

$<r>={\frac {a_{0}}{2}}(3n^{2}-l(l+1))$

כאשר $a_{0}$ הוא רדיוס בוהר. ניתן לראות שהקטנת המספר הקוונטי הזוויתי l מגדילה את $<r>$ עד לערך מקסימלי של ${\frac {3a_{0}}{2}}n^{2}$ המתקבל עבור המצב העצמי הסימטרי כדורית של רמת האנרגיה ה-n. ניתן להראות גם שהמרחקים "המותרים" $r_{n}$ של רמות האנרגיה של האלקטרון במודל בוהר של אטום המימן הם השכיח של פונקציית צפיפות ההסתברות של r כפי שמתקבלת במודל שרדינגר, כלומר $r_{n}$ הוא המרחק שבו $f_{n}(r)=4\pi r^{2}|R_{n}(r)|^{2}$ מקבלת ערך מקסימלי.

נוסף על כך, מכיוון שההפרש $E-V_{eff}(r)$ קובע למעשה את האנרגיה הקינטית הרדיאלית של החלקיק, ומכאן גם את מספר הגל הרדיאלי $\kappa _{r}$, ניתן לשער שמספר הצמתים (שורשים של $R(r)$) בחלק הרדיאלי יגדל עם הקטנת L. למשל, בפתרון המתמטי המדויק של אטום המימן, פונקציית הגל הרדיאלית שווה לאקספוננט דועך כפול פולינום לגר מוכלל, אשר מספר שורשיו עולה עם הקטנת L.

פתרונות עבור פוטנציאלים מסוימים

פרק זה לוקה בחסר. אנא תרמו לוויקיפדיה והשלימו אותו. ייתכן שתמצאו פירוט בדף השיחה.

ראו גם

• אטום המימן