במתמטיקה , פולינומי לז'נדר הם פולינומים אורתוגונליים המהווים את סדרת הפתרונות למשוואת לז'נדר :
d
d
x
[
(
1
−
x
2
)
d
d
x
P
n
(
x
)
]
+
n
(
n
+
1
)
P
n
(
x
)
=
0.
{\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P_{n}(x)\right]+n(n+1)P_{n}(x)=0.}
הפולינומים נקראים על שם ה
מתמטיקאי ה
צרפתי אדריאן-מארי לז'נדר .
המשוואות הדיפרנציאליות הרגילות הללו מופיעות באופן טבעי במגוון בעיות פיזיקליות, בפרט, בפתרון
משוואת לפלס ב
קואורדינטות כדוריות .
למשוואה זו נקודות סינגולריות רגולריות (Regular Singular Point) ב-
x
=
±
1
{\displaystyle x=\pm 1}
טור חזקות (שיטת פרובניוס ). הנירמול הסטנדרטי הוא:
P
n
(
1
)
=
1
{\displaystyle \ P_{n}(1)=1}
את הפולינום ה-
n
{\displaystyle n}
נוסחת רודריגז :
P
n
(
x
)
=
1
2
n
n
!
d
n
d
x
n
[
(
x
2
−
1
)
n
]
.
{\displaystyle P_{n}(x)={1 \over 2^{n}n!}{d^{n} \over dx^{n}}\left[(x^{2}-1)^{n}\right].}
להלן רשימת אחד עשר הפולינומים הראשונים (כלומר, עד n=10):
n
P
n
(
x
)
{\displaystyle P_{n}(x)\,}
0
1
{\displaystyle 1\,}
1
x
{\displaystyle x\,}
2
1
2
(
3
x
2
−
1
)
{\displaystyle {\begin{matrix}{\frac {1}{2}}\end{matrix}}(3x^{2}-1)\,}
3
1
2
(
5
x
3
−
3
x
)
{\displaystyle {\begin{matrix}{\frac {1}{2}}\end{matrix}}(5x^{3}-3x)\,}
4
1
8
(
35
x
4
−
30
x
2
+
3
)
{\displaystyle {\begin{matrix}{\frac {1}{8}}\end{matrix}}(35x^{4}-30x^{2}+3)\,}
5
1
8
(
63
x
5
−
70
x
3
+
15
x
)
{\displaystyle {\begin{matrix}{\frac {1}{8}}\end{matrix}}(63x^{5}-70x^{3}+15x)\,}
6
1
16
(
231
x
6
−
315
x
4
+
105
x
2
−
5
)
{\displaystyle {\begin{matrix}{\frac {1}{16}}\end{matrix}}(231x^{6}-315x^{4}+105x^{2}-5)\,}
7
1
16
(
429
x
7
−
693
x
5
+
315
x
3
−
35
x
)
{\displaystyle {\begin{matrix}{\frac {1}{16}}\end{matrix}}(429x^{7}-693x^{5}+315x^{3}-35x)\,}
8
1
128
(
6435
x
8
−
12012
x
6
+
6930
x
4
−
1260
x
2
+
35
)
{\displaystyle {\begin{matrix}{\frac {1}{128}}\end{matrix}}(6435x^{8}-12012x^{6}+6930x^{4}-1260x^{2}+35)\,}
9
1
128
(
12155
x
9
−
25740
x
7
+
18018
x
5
−
4620
x
3
+
315
x
)
{\displaystyle {\begin{matrix}{\frac {1}{128}}\end{matrix}}(12155x^{9}-25740x^{7}+18018x^{5}-4620x^{3}+315x)\,}
10
1
256
(
46189
x
10
−
109395
x
8
+
90090
x
6
−
30030
x
4
+
3465
x
2
−
63
)
{\displaystyle {\begin{matrix}{\frac {1}{256}}\end{matrix}}(46189x^{10}-109395x^{8}+90090x^{6}-30030x^{4}+3465x^{2}-63)\,}
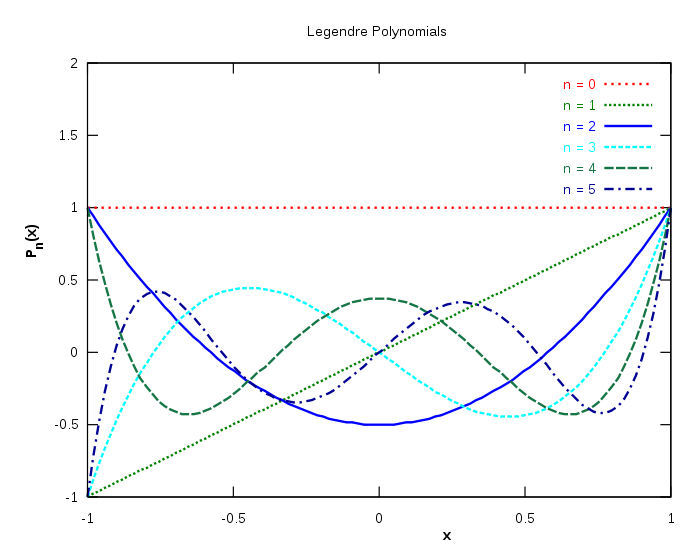
להלן גרף של ששת הפולינומים הראשונים, בתחום 1>|x|.
סדרות רבות של פונקציות המהוות פתרון למשוואה דיפרנציאלית מקיימות תנאי אורתוגונליות עבור מכפלה פנימית מסוימת (מרחב הילברט ). לרוב, לכל סדרת פונקציות בנפרד יש מכפלה פנימית שונה עבורה הסדרה אורתוגונלית. המכפלה הפנימית עבורה פולינומי לז'נדר הם אורתוגונליים נתונה על ידי:
∫
−
1
1
P
m
(
x
)
P
n
(
x
)
d
x
=
2
2
n
+
1
δ
m
n
{\displaystyle \int _{-1}^{1}P_{m}(x)P_{n}(x)\,dx={2 \over {2n+1}}\delta _{mn}}
כאשר
δ
{\displaystyle \ \delta }
הדלתא של קרונקר .
ניתן להגיע אל הפולינומים בעזרת תהליך גרם-שמידט עבור חזקות שלמות של
x
{\displaystyle \ x}
הפונקציה היוצרת , של פולינומי לז'נדר היא:
1
1
+
η
2
−
2
η
x
=
∑
k
=
0
∞
η
k
P
k
(
x
)
{\displaystyle {\frac {1}{\sqrt {1+\eta ^{2}-2\eta x}}}=\sum _{k=0}^{\infty }\eta ^{k}P_{k}(x)}
בנוסף לנוסחת חישוב כללית (המצריכה בעצם פעולת צעד-צעד, היות שצריך לחשב נגזרות מסדרים גבוהים), ישנה אפשרות לחשב את פולינומי לז'נדר בעזרת נוסחה רקורסיבית, כלומר, נוסחה המחשבת פולינום מסדר מסוים בעזרת הפולינומים הקודמים לו. נוסחת הרקורסיה נתונה על ידי:
P
n
(
x
)
=
1
n
(
(
2
n
−
1
)
x
P
n
−
1
(
x
)
−
(
n
−
1
)
P
n
−
2
(
x
)
)
{\displaystyle P_{n}(x)={\frac {1}{n}}((2n-1)xP_{n-1}(x)-(n-1)P_{n-2}(x))\,}
הצגה אינטגרבילית של פולינום לז'נדר:
P
n
(
z
)
=
1
2
π
i
∫
(
1
−
2
t
z
+
t
2
)
1
/
2
t
−
n
−
1
d
t
{\displaystyle P_{n}(z)={\frac {1}{2\pi i}}\int (1-2tz+t^{2})^{1/2}t^{-n-1}dt}
פולינומי לז'נדר שימושיים מאוד בפיזיקה ומשמשים למגוון חישובים. הידועים שבהם הם בתחום האלקטרוסטטיקה ותורת הקוונטים .
Φ
(
r
,
θ
)
=
∑
ℓ
=
0
∞
[
A
ℓ
r
ℓ
+
B
ℓ
r
−
(
ℓ
+
1
)
]
P
ℓ
(
cos
θ
)
{\displaystyle \Phi (r,\theta )=\sum _{\ell =0}^{\infty }\left[A_{\ell }r^{\ell }+B_{\ell }r^{-(\ell +1)}\right]P_{\ell }(\cos \theta )}
כאשר המקדמים
A
ℓ
{\displaystyle A_{\ell }}
B
ℓ
{\displaystyle B_{\ell }}
כאשר רוצים לחשב את הפוטנציאל החשמלי של מטען נקודתי אשר איננו נמצא בראשית מערכת צירים (במערכת קואורדינטות כדורית), ניתן לחשבו בעזרת (שימו לב שמדובר בפרופורציוניות ולא בשיויון):
Φ
(
r
,
θ
)
∝
1
R
=
1
r
2
+
a
2
−
2
a
r
cos
θ
.
{\displaystyle \Phi (r,\theta )\propto {\frac {1}{R}}={\frac {1}{\sqrt {r^{2}+a^{2}-2ar\cos \theta }}}.}
את הפונקציה הזו ניתן לחשב בעזרת פולינומי לז'נדר לפי הצורה הבאה:
Φ
(
r
,
θ
)
∝
1
r
∑
k
=
0
∞
(
a
r
)
k
P
k
(
cos
θ
)
{\displaystyle \Phi (r,\theta )\propto {\frac {1}{r}}\sum _{k=0}^{\infty }\left({\frac {a}{r}}\right)^{k}P_{k}(\cos \theta )}
פולינומי לז'נדר משמש בנוסף כפתרון לחלק הזוויתי (הזווית הנפתחת מציר ה-z) של משוואת שרדינגר עבור מקרה של פוטנציאל מרכזי . במקרה זה, ישנה גם תלות במרחק מהראשית r וכן בזווית סביב ציר z (החלק האזימותלי). את התלות המשותפת בשתי הזוויות ניתן להציג בעזרת הרמוניות ספריות . נסתכל על המשוואה הדיפרנציאלית הבאה:
d
d
x
[
(
1
−
x
2
)
d
y
d
x
]
+
(
n
(
n
+
1
)
−
m
2
1
−
x
2
)
y
=
0.
{\displaystyle {d \over dx}\left[(1-x^{2}){dy \over dx}\right]+\left(n(n+1)-{\frac {m^{2}}{1-x^{2}}}\right)y=0.}
עבור
m
=
0
{\displaystyle m=0}
נקבל את משוואת לז'נדר הרגילה. פתרון המשוואה באופן כללי מניב את פולינומי לז'נדר הנלווים
P
l
m
(
x
)
{\displaystyle P_{l}^{m}(x)}
וניתן לחשב אותם בצורה הבאה על ידי שימוש בנוסחת רודריגז:
P
l
m
(
x
)
=
(
−
1
)
m
2
l
l
!
(
1
−
x
2
)
m
2
d
l
+
m
d
x
l
+
m
(
x
2
−
1
)
l
{\displaystyle P_{l}^{m}(x)={\frac {(-1)^{m}}{2^{l}l!}}(1-x^{2})^{\frac {m}{2}}{d^{l+m} \over dx^{l+m}}(x^{2}-1)^{l}}
הרמוניות הספריות , ויחס האורתוגונליות ביניהם הוא:
∫
−
1
1
P
k
m
P
ℓ
m
d
x
=
2
(
ℓ
+
m
)
!
(
2
ℓ
+
1
)
(
ℓ
−
m
)
!
δ
k
,
ℓ
{\displaystyle \int _{-1}^{1}P_{k}^{m}P_{\ell }^{m}dx={\frac {2(\ell +m)!}{(2\ell +1)(\ell -m)!}}\ \delta _{k,\ell }}


![{\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P_{n}(x)\right]+n(n+1)P_{n}(x)=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd51c7228067db4bea119843fb19c6caab834954)



![{\displaystyle P_{n}(x)={1 \over 2^{n}n!}{d^{n} \over dx^{n}}\left[(x^{2}-1)^{n}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9414fbe11099d281205ca2a2f051f405c2d348c)


















![{\displaystyle \Phi (r,\theta )=\sum _{\ell =0}^{\infty }\left[A_{\ell }r^{\ell }+B_{\ell }r^{-(\ell +1)}\right]P_{\ell }(\cos \theta )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d24d50b1e919e533be6a3cf69a56ee68bc96bf61)




![{\displaystyle {d \over dx}\left[(1-x^{2}){dy \over dx}\right]+\left(n(n+1)-{\frac {m^{2}}{1-x^{2}}}\right)y=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71d1eb1df22fad12c57a7d2fa214d47987651324)



