מעטפת (מתמטיקה)
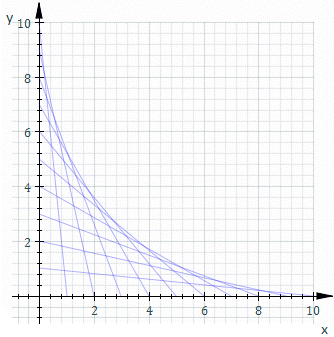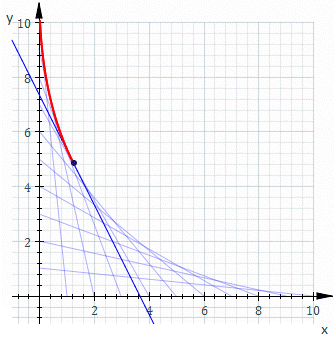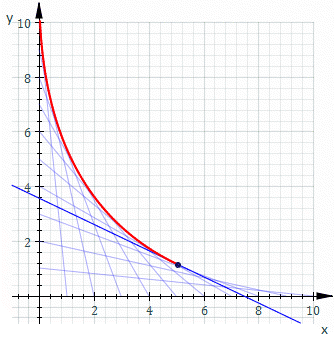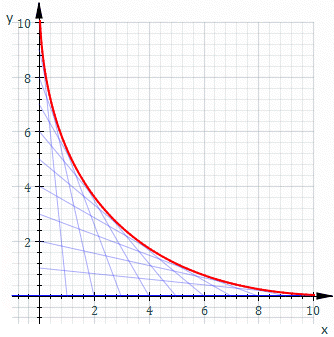
בגאומטריה, המעטפת (באנגלית: Envelope) של משפחה של עקומים במישור היא העקום אשר משיק לכל עקום במשפחה הזו בנקודה כלשהי. באופן קלאסי, ניתן לחשוב על נקודה על המעטפת כנקודת החיתוך של שני עקומים "סמוכים", כלומר הגבול של נקודות החיתוך של עקומים סמוכים. המעטפת של משפחת העקומים "תוחמת" את משפחת העקומים, במובן שכל נקודה על כל עקום כלשהו השייך למשפחה נמצאת בתוך האזור התחום על ידי המעטפת. הרעיון הזה יכול להיות מוכלל למעטפת של משטחים במרחב, וכך הלאה לממדים גבוהים יותר.
באופטיקה גאומטרית, הקאוסטיקה היא המעטפת של משפחה של קרני אור, כפי שניתן לראות באיור.
תיאור מתמטי: מעטפת של משפחה של עקומים[עריכת קוד מקור | עריכה]
נניח שכל עקום Ct במשפחה נתון כפתרון של המשוואה ft(x, y)=0 (ראו עקום בלתי מפורש), כאשר t הוא פרמטר. נכתוב F(t, x, y)=ft(x, y) ונניח ש-F גזירה.
המעטפת של המשפחה Ct מוגדרת כאוסף הנקודות עבורם מתקיים : עבור ערך כלשהו של t.
משמעות התנאי הראשון היא שהנקודה (x,y) נמצאת על העקום Ct, ומשמעות התנאי השני היא שכאשר נעים אל העקום Ct+dt הנקודה (x,y) נותרת קבועה במקומה, דהיינו (x,y) היא נקודת החיתוך של העקומים Ct ו-Ct+dt, כלומר הגבול של נקודות החיתוך של העקום Ct עם עקומים סמוכים. התנאי השני אינו מובן מאליו כלל וכלל שכן עבור נקודות אחרות (שלא על המעטפת) מתקיים שהשינוי ב-F(t, x, y) שווה לאפס עבור שינוי משולב ב-t, x ו-y.
מקרה פרטי חשוב הוא כאשר F(t, x, y) הוא פולינום ב-t. מקרה זה כולל, באמצעות סילוק המכנים, את המקרה ש-F(t, x, y) הוא פונקציה רציונלית ב-t. במקרה זה, מן ההגדרה ניתן להסיק ש-t הוא שורש כפול של F(t, x, y), ומשוואת המעטפת ניתנת למציאה באמצעות השוואה בין הדיסקרימיננטה של F ל-0.
לשם דוגמה, יהי Ct הקו הישר אשר משוואתו היא מהצורה:
. אם נסלק את השברים נקבל: :. כלומר עבור כל נקודה (x,y) יש לכל היותר שני ערכים של t עבורם הישר המתאים עובר דרך הנקודה (x,y), ואינטואיציה גאומטרית עוזרת להבין זאת, כי קיים בוודאות ישר אחד שעובר דרך הנקודה (הישרים מכסים יחדיו את כל האזור התחום על ידי המעטפת) ולאחר מכן ניתן "לנוע" לאורך הישר הנתון באמצעות נקודות החיתוך עם ישרים סמוכים עד שמגיעים לנקודה הנ"ל. אולם, נקודות (x,y) הנמצאות על המעטפת מוגדרות כגבול של נקודות חיתוך של עקומים "סמוכים" ולפיכך לכל נקודה על הגבול יש בדיוק ישר אחד שעובר דרכה. המשמעות היא שלמשוואה הריבועית לעיל יש פתרון יחיד t, ולפיכך המעטפת היא אוסף כל הנקודות (x,y) עבורם למשוואה הריבועית: יש פתרון יחיד. לפיכך משוואת המעטפת היא הדיסקרימיננטה של המשוואה הריבועית שווה לאפס::.
דוגמאות[עריכת קוד מקור | עריכה]

- סולם שמונח על קיר במקביל לקיר, ומתחיל להחליק כך שקצה אחד שלו נמצא על הקיר האנכי וקצה אחר שלו על הרצפה יתווה מעטפת של אסטרואידה (האוולוט של האליפסה), כלומר האסטרואידה היא המעטפת של כל המצבים של הסולם בזמנים שונים. בניסוח מתמטי, האסטרואידה היא המעטפת של משפחה של קווים ישרים המחברים את הנקודות , ו- כאשר , כמוראה באיור.
הוכחה: משפחת הישרים היא אוסף כל הישרים שמשוואתם מהצורה כאשר t בין 0 ל-1 (כולל). המעטפת של משפחת הישרים היא אוסף כל הנקודות שמקיימות . לכן:
לכן, אחרי העברת אגפים והוצאת מכנה משותף, נקבל:
ומהצבה בביטוי ל-Y כפונקציה של X נקבל:
ומכאן , וזוהי משוואת האסטרואידה.
יישומים[עריכת קוד מקור | עריכה]
משוואות דיפרנציאליות רגילות[עריכת קוד מקור | עריכה]
מעטפות גאומטריות קשורות למחקר של משוואות דיפרנציאליות רגילות, ובאופן מיוחד בהקשר של פתרונות סינגולריים למד"ר. ניקח, כדוגמה, את המשפחה בת פרמטר אחד של קווים משיקים לפרבולה y = x2. אלה מתקבלים באמצעות המשפחה היוצרת F(t,(x,y)) = t2 – 2tx + y. הצבת רמת האפס F(t0,(x,y)) = 0 נותנת את המשוואה של המשיק לפרבולה בנקודה (t0,t02). המשוואה t2 – 2tx + y = 0 ניתנת תמיד לפתרון בצורה של y כפונקציה של x ולכן:
הצבה :
נותנת את המד"ר:
באופן לא מפתיע, y = 2tx − t2, כולם פתרונות למד"ר הזו. כמו כן, גם המעטפת של המשפחה בת-פרמטר אחד של קווים אלו, שהיא הפרבולה y = x2, היא פתרון למד"ר הזו.
קאוסטיקות[עריכת קוד מקור | עריכה]

באופטיקה גאומטרית, הקאוסטיקה היא המעטפת של משפחה של קרני אור. בתמונה זו ישנה קשת של מעגל. קרני האור מגיעות ממקור "באינסוף" ולכן מגיעות מקבילות. כשהן פוגעות בקשת המעגלית קרני האור מפוזרות בכיוונים שונים לפי חוק ההחזרה. כשקרן אור פוגעת בקשת בנקודה האור יוחזר כאילו הוא היה מוחזר על ידי הקו המשיק לקשת בנקודה זו. המעטפת של הקווים הללו נקרא הקאוסטיקה הרפלקטיבית. קאוסטיקה רפלקטיבית תהיה מורכבת באופן גנרי מנקודות חלקות ונקודות חוד (cusp).
מנקודת המבט של חשבון הווריאציות, עקרון פרמה (בצורתו המודרנית) קובע כי קרני האור הם אקסטרמלים של פונקציונל האורך:
לאורך העקום החלק γ ב-[a,b], עם נקודות קצה γ(a) ו-γ(b). הקאוסטיקה הנוצרת על ידי נקודה נתונה P (בתמונה הנקודה היא באינסוף) היא האוסף של conjugate points ל-P.
עקרון הויגנס[עריכת קוד מקור | עריכה]
אור עשוי לנוע דרך תווך לא איזוטרופי ולא הומוגני בקצבים שונים בתלות בכיוון ונקודת המיקום ההתחלתי של הקרן. השפה של האזור אליו אור יכול לנוע מנקודה נתונה q אחרי זמן t נקראת חזית הגל אחרי זמן t, ומסומנת כאן Φq(t). היא מורכבת בדיוק מאותן הנקודות שניתן להגיע אליהן מ-q בזמן t באמצעות תנועה במהירות האור (שעשויה לשתנות בחומר). עקרון הויגנס מאשר שאוסף חזיתות הגלים (Φq0(s + t הוא המעטפת של משפחה של חזיתות גלים Φq(s עבור q ∈ Φq0(t). באופן כללי יותר, הנקודה q0 יכולה להיות מוחלפת בכל עקום, משטח או קבוצה סגורה במרחב.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- מעטפת, באתר MathWorld (באנגלית)
- מעטפת, באתר אנציקלופדיה בריטניקה (באנגלית)


















![{\displaystyle L[\gamma ]=\int _{a}^{b}|\gamma '(t)|\,dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/55e0ba36224ef5f161983c131764c4cbc80410f7)