תורת הבקרה
תורת הבקרה היא נושא רב תחומי, אשר בא לידי ביטוי במערכות שונות (ביולוגיות, מכניות, רובוטיות, אוויוניות ועוד) תחת ייצוג מתמטי זהה. ככל שהתהליכים בתעשייה נעשים מורכבים יותר, כך יש צורך בבקרה הדוקה ומדויקת יותר על התהליך. מערכות הבקרה נפוצות כמעט בכל תהליך פיזיקאלי, כגון בקרת מפלס, זרימה, טמפרטורה, מתח, זרם חשמלי, ריכוז מוצקים בנוזל, מסלול, וטיסה.
מערכת בקרה היא מנגנון אשר שולט על יציבות תהליך של מערכת אחרת, עליה ברצוננו לשלוט.
על מנת להתמודד עם הפער בין הערך המצוי לערך הרצוי של מערכות, נדרשת פעולה לתיקון סטיות של המשתנה המבוקר (גודל פיזיקלי) מערכו הרצוי. סטיות אלה נגרמות עקב הפרעות במערכת.
לדוגמה: מזגן - כאשר נגדיר טמפרטורה רצויה, המזגן ימשיך לפעול כל עוד לא התקבלה התוצאה הרצויה ויפסיק את עבודתו בעת קבלת התוצאה הרצויה.
רכיבי מערכת הבקרה[עריכת קוד מקור | עריכה]
מערכת בקרה כוללת את הרכיבים הבסיסיים הבאים:
- יחידת מדידה (measuring or monitoring unit), המודדת ומגיבה לשינויים במשתנה או בתהליך המבוקר, כמו שינוי הטמפרטורה, הלחץ, מהירות הסיבוב וכו'.
- בקר (controller), האומד את גודל השגיאה או הסטייה בין הערך הנמדד לערך הרצוי של המשתנה או התהליך המבוקר, ושולח אות תיקון למנגנון ההפעלה.
- משוב או הפעלה (actuator), המאפשר תיקון. למשל שסתום בקרה פנאומטי, הנשלט על ידי לחץ אוויר ופותח או סוגר מעבר נוזל, מפסק חשמלי המפעיל או מדמים מנוע חשמלי.
סוגי מערכות הבקרה[עריכת קוד מקור | עריכה]
את מערכות הבקרה מסווגים לשני סוגים עיקריים:
- מערכת בקרה בחוג פתוח, בה אין משוב מיחידת המדידה אל מנגנון ההפעלה באשר לתוצאות הביצוע של התהליך. למשל: חימום אוכל במיקרוגל תלוי אך ורק בזמן שהגדרנו ולא למצב האוכל אחרי הפעולה.
- מערכת בקרה בחוג סגור, שבה תלויה פעולת התיקון של הבקר במשוב של תוצאת התהליך המבוקר. יחידת המדידה, המודדת את תוצאות התהליך, משפיעה בצורה ישירה על מנגנון התיקון או ההפעלה. המשוב הוא קבלת מידע עדכני על מצב המערכת ותנאי הסביבה. המשוב מבצע עדכון של פקודות הפעולה. למשל: מזגן ביתי.
דיאגרמת מלבנים[עריכת קוד מקור | עריכה]
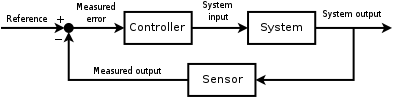
נהוג להגדיר את תהליך המערכת באמצעות דיאגרמת מלבנים. דיאגרמת המלבנים מתארת את התהליך מהכנסת הכניסה (reference) ועד לקבלת הערך המצוי (system output). בעזרת דיאגרמת מלבנים אפשר לתאר רכיבים במערכת הבקרה. כל רכיב במערכת הבקרה יוצג במלבן.
את דיאגרמת המלבנים ניתן להמיר לפונקציית תמסורת, המתארת את היחס בין הערך המצוי לכניסה. ערך הכניסה הוא האילוץ. הוא יכול להיות אילוץ מדרגה (פועל/לא פועל), אילוץ שיפוע (הגברה/הנמכה), אילוץ הלם (אות בדיד), אילוץ סינוס (מתח AC) וכו'.
פונקציית תמסורת[עריכת קוד מקור | עריכה]
 ערך מורחב – פונקציית תמסורת
ערך מורחב – פונקציית תמסורת

פונקציית התמסורת היא פונקציה המתארת את היחס בין הערך הנכנס לתהליך לערך היוצא ממנו.
כך למשל, אם ניקח מנגנון שבו קיימת כניסה ויציאה . ניתן לתאר את פונקציית התמסורת כך:
מכאן נקבל שפונקציית התמסורת של המערכת היא:
את פונקציית התמסורת מקבלים מתוך משוואת המצב של המערכת. בבקרה קלאסית ועבור מערכות של כניסה אחת ויציאה אחת מקובל למדל את המערכת באמצעות התמרת לפלס. בשיטות מודרניות יותר מקובל למדל במישור הזמן על ידי מרחב המצב.
בקרת PID[עריכת קוד מקור | עריכה]

בקרה נפוצה של מערכות ליניאריות היא בקרת PID:
- P - פרופורציונלי - מתקן את השגיאה העכשווית בצורה פרופורציונלית לשגיאה
- I - אינטגרלי - מוסיף תיקון פרופורציונלי לאינטגרל בזמן על שגיאת העקיבה ובכך מבטיח שגיאת מצב מתמיד אפסית
- D - דיפרנציאלי - מוסיף תיקון פרופורציונלי לנגזרת בזמן של השגיאה ובכך מוסיף ריסון למערכת ומונע תגובת יתר (overshoot). היא לעולם אינה מגיעה לבד, כלומר תמיד תהיה ID או PD, כיוון שבמצב כזה לא תתקן שגיאה קבועה במערכת. בנוסף, היא עלולה להפחית את יציבות המערכת בשל רגישותה לרעשים.
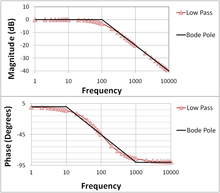
עקומת בודה - עקומי בודה הם דרך נוחה להסתכלות על תגובת האמפליטודה ותגובת התדר של מערכת. באמצעות שימוש בתכונות הלוגריתם מפרקים את פונקציית התמסורת לסכומים והפרשים כך שניתן לצייר את התוצאה ללא קושי.
בין השיטות הנפוצות לבקרת PID נמנית שיטת זיגלר ניקולס.
קביעת יציבות של מערכת[עריכת קוד מקור | עריכה]
קיימות שיטות שונות לבדיקת יציבות של מערכת:
- קריטריון ראוט-הורוביץ
- דיאגרמת נייקוויסט - באמצעות התבוננות בעקום הנייקוויסט של החוג הפתוח, ניתן לקבוע תנאים ליציבות החוג הסגור. קריטריון נייקוויסט לא מצריך ידיעת הקטבים של תמסורת החוג הסגור לשם קביעת היציבות.
- שיטת מיקום גאומטרי של שורשים (מג"ש, Root Locus(אנ')) - מתארים באופן גרפי את תזוזת שורשי הפולינום האופייני (קטבי התמסורת) כתלות בהגבר הקבוע. בהינתן פונקציית תמסורת של החוג הפתוח ובעזרת שיטת לוקוס השורשים, ניתן למצוא את מיקום קטבי החוג הסגור עבור הגבר כלשהו.
- שימוש בפונקציית קאפא
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- תורת הבקרה, באתר אנציקלופדיה בריטניקה (באנגלית)
- תורת הבקרה, באתר MathWorld (באנגלית)
 בקרה, תיאוריה, דף שער בספרייה הלאומית
בקרה, תיאוריה, דף שער בספרייה הלאומית








