מכניקה לגראנז'ית

ז'וזף-לואי לגראנז'. המפתח של המכניקה הלגראנז'ית.

במכניקה אנליטית, מכניקה לגראנז'ית היא ניסוח חלופי למכניקה הקלאסית - בכך היא שקולה למכניקה הניוטונית, למכניקה ההמילטונית ולמשוואת המילטון-יעקובי. המכניקה הלגראנז'ית הוצגה לראשונה על ידי ז'וזף-לואי לגראנז' בספרו מכניקה אנליטית מ-1788, כשאת העקרונות לפיתוחה תרמו ד'אלמבר, מופרטווי ואוילר, לפני לגראנז', והמילטון לאחריו.

בתיאור הלגראנז'י המערכת מתוארת על ידי מרחב קונפיגורציות $M$ ופונקציה חלקה $L:TM\times \mathbb {R} _{t}\to \mathbb {R}$ (כאשר $TM$ הוא מרחב לקט המשיקים ל-$M$ (Tangent bundle) ו-$\mathbb {R} _{t}\subseteq \mathbb {R}$ מתאר את משתנה הזמן). כלומר הפונקציה $L(\mathbf {q} ,\mathbf {v} ,t)$ הנקראת הלגראנז'יאן של המערכת, היא פונקציה של הנקודה במרחב הקונפיגורציה - $\mathbf {q} \in M$, המהירות המשיקה למרחב הקונפיגורציה בנקודה $\mathbf {q}$ - $\mathbf {v} \in T_{\mathbf {q} }M$ והזמן - $t$. את אופי התנועה של המערכת ניתן לנבא מהתכונות של הלגראנז'יאן, וניתן לגזור ממנו משוואות תנועה דיפרנציאליות הנקראות משוואות אוילר-לאגראנז'.

בבעיות רגילות במכניקה קלאסית, מרחב הקונפיגורציות $M$ הוא מרחב מממד סופי. הרחבה של המכניקה הלגראנז'ית למצב בו המרחב $M$ הוא מממד אינסופי מאפשרת פיתוח של תורת שדות קלאסיים. הקלות היחסית של המעבר מממד סופי לממד אינסופי בניסוח הלגראנז'י הופך אותו לניסוח המועדף המשמש בפיתוח תורת שדות קוונטים.

למכניקה הלגראנז'ית קשר רב עם סימטריות וחוקי שימור, קשר שמנוסח במשפט נתר. קשר זה עובד לשני הכיוונים - אם הלגראנז'יאן ידוע ניתן להשתמש בקשר כדי למצוא את הסימטריות והגדלים הנשמרים במערכת; אם הסימטריות של המערכת ידועות, ניתן להשתמש בהן כדי לכתוב ביטוי ללגראנז'יאן.

רקע

בשנת 1687, פרסם אייזק ניוטון את ספרו פרינקיפיה, והציג את היסודות של המכניקה הקלאסית. לפי התיאוריה הניוטונית, על גופים במערכת מכנית פועלים כוחות, והתאוצה של הגופים השונים פרופרציונלית לכוחות אלו. ניוטון אף הראה שהכוח הגרביטציוני הפועל בין שני גופים פרופורציונלי לאחד חלקי ריבוע המרחק. בסוף המאה ה-17 ותחילת המאה ה-18, התיאוריה של ניוטון התפשטה ברחבי אירופה ומדענים רבים החלו לפתור באמצעותה בעיות מכניות. ב-1736 פרסם אוילר את ספרו מכניקה שהציג את חוקי התנועה של ניוטון כמשוואות דיפרנציאליות, והרחיב את חוקי התנועה כדי לתאר את תנועתם של גופים קשיחים. בשנים האלו, פתרון בעיות במכניקה התמקד בכתיבת התאוצה כפונקציה של המיקום של הגופים במערכת וניסיון לפתור את המשוואה הדיפרנציאלית המתקבלת לתנועת הגופים. הבעיה שעלתה בגישה זו היא שבמקרים מסוימים מציאת הכוחות הפועלים על הגוף היא בעיה כשלעצמה. סוג מיוחד של בעיות כאלו הן בעיות בהן קיים אילוץ על המערכת, לדוגמה בעיות בהן הגוף מוגבל לתנועה על משטח מסוים. בבעיות כאלה, הכוח שהמשטח יפעיל על החלקיק, יהיה כזה שיחייב את החלקיק להמשיך לנוע על המשטח. אולם משוואות התנועה של ניוטון לא מספקות דרך סדורה למצוא את הכוח הזה.

ז'אן לה רון ד'אלמבר. העיקרון שהציג משמש כבסיס לפיתוח התיאוריה הלגראנז'ית.

המכניקה הלגראנז'ית פותחה כדי לספק דרך לפתור בעיות בהן קיימים אילוצים, וזאת באחת משתי דרכים - הצגת דרך סדורה למציאת הכוחות אותם מפעילים האילוצים או מציאת דרך לכתיבת משוואות התנועה של המערכת בלי למצוא באופן ישיר את הכוחות האלה. את בסיסו של הפורמליזם הלגראנז'י ניתן לראות בעקרון העבודה הווירטואלית שנוסח מתמטית על ידי יוהאן ברנולי בשנת 1725, ובהרחבתו לעקרון ד'אלמבר שהוצג על ידי ד'אלמבר ב-1743. עיקרון זה עוסק בהעתקות וירטואליות - הזזה של מיקום הגופים במערכת באופן אינפיניטסימלי ומיידי. העיקרון מצביע על כך שבמקרים רבים הכוחות אותם מפעילים האילוצים לא מבצעים עבודה וירטואלית על המערכת, כלומר ההטלה של הכוח על ההעתקה הווירטואלית היא אפס. לכן, הכוחות הללו שונים מהכוחות הרגילים במערכת, שמפעילים עבודה וירטואלית המתאזנת עם ההטלה של הנגזרת הזמנית של התנע על ההעתקה הווירטואלית. את ההבחנה הזו פיתח לגראנז', ובאמצעות שימוש בקואורודינטות מוכללות, הפך אותה למשוואות תנועה שניתנות לפתרון באופן סדור.

בעיית הברכיסטוכרון. הבעיה שואלת מהי צורת העקומה שתביא את הכדור מנקודה לנקודה בזמן המינימלי. חשבון וריאציות מספק אחת הדרכים לפתרון הבעיה.

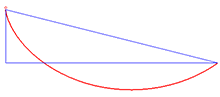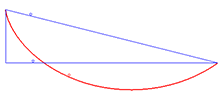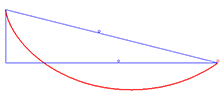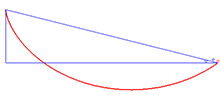
בין הכלים המתמטיים שפותחו בראשית המאה ה-18 כדי לפתור בעיות במכניקה, התפתח התחום של חשבון וריאציות. תחום זה עוסק במציאת נקודות קיצון עבור פונקציונלים. כדוגמה לבעיה בחשבון וריאציות ניתן להסתכל על בעיית הברכיסטוכרון, המחפשת את צורת העקומה שלאורכה חרוז המחליק בהשפעת כוח הכבידה וללא חיכוך יגיע באופן המהיר ביותר מנקודה מסוימת לנקודה אחרת. ב-1662, הציג פרמה את העיקרון העומד מאחורי תנועתם של קרני אור אופטיות. לפי עקרון פרמה, קרניים כאלה יטיילו מנקודה לנקודה לאורך המסלול בו זמן התנועה יהיה הקצר ביותר. פרמה השתמש בעיקרון זה כדי להסביר את חוקי השבירה של סנל. ב-1744 מופרטווי שאל מדוע האור יעדיף את המסלול בעל הזמן הקצר ביותר, ולא את המסלול בעל הדרך הקצרה ביותר. הוא המשיך והראה שאם בוחרים את המסלול בו הדרך קצרה ביותר, כאשר משקללים את המרחק לפי המהירות, מתקבל חוק סנל. עוד באותה שנה, אוילר טען שתנועה של חלקיקים במערכת מכנית היא במסלול בו תנועת החלקיקים עוברת את הדרך הקצרה ביותר לפי שקלול הכולל את התנע שלהם. חוק זה מתקבל במצב בו כל הכוחות במערכת הם כוחות משמרים. ב-1746 מופרטווי התייחס לעבודתו של אוילר, ואמר שאוילר השתמש בעקרון שהוא הציג למערכות מכניות; על אף שמופרטווי הציג את העיקרון כעקרון אופטי ולא מכני, העיקרון הזה נקרא על שמו של מופרטווי. בספרו מכניקה אנליטית משנת 1788, הראה לגראנז' כיצד עקרון מופרטווי נובע מעקרון ד'לאמבר. ויליאם רואן המילטון הרחיב את העיקרון למערכות בהן הכוחות לא משמרים, אבל ניתנים להצגה באמצעות פונקציית לגראנז'יאן. העיקרון הזה נקרא עקרון המילטון או עקרון הפעולה הסטציונרית. לפי עיקרון זה הפעולה של המערכת, המוגדרת כאינטגרל של פונקציית הלגראנז'יאן לפי הזמן לאורך המסלול, מקבלת ערך מינימום במסלול בו החלקיק ינוע. את משוואות התנועה שלגראנז' הציג, ניתן לפתח ישירות מעקרון ד'אלמבר, או מחשבון וריאציות בניסיון למצוא את המסלול שנותן לפעולה ערך סטציונרי לפי עקרון המילטון.

עקרון ד'אלמבר

ערך מורחב – עקרון ד'אלמבר

היסטורית, הפיתוח של עקרונות המכניקה הלגראנז'ית יוצא מעקרון ד'אלמבר. עיקרון זה נובע משימוש בחוקי התנועה של ניוטון והפעלתם על עקרון העבודה הווירטואלית. העתקה וירטואלית, היא קונספט מתמטי המתאר תזוזה קטנה של המערכת ללא הזזה של פרמטר הזמן, לא כל שינוי של המערכת אפשרי, לדוגמה במנוף מכני, תזוזה של צד אחד של המנוף כלפי מטה, מחייבת שהצד השני יעלה מעלה, רק העתקות שאפשריות מבחינת המערכת נחשבות העתקות וירטואליות. עבודה וירטואלית היא הטלה של הכוחות הפועלים במערכת על העתקות וירטואליות. עקרון עבודה הווירטואלית עוסק בכוחות הפועלים על מערכת הנמצאת בשיווי משקל סטטי וקובע שאם המערכת נמצאת בשיווי משקל כזה, העבודה הווירטואלית מתאפסת תמיד. ד'אלמבר הרחיב את עקרון ההעתקה הווירטואלית, וטען שאם המערכת נעה, הרי שהעבודה הווירטואלית צריכה להתאזן עם האינרציה של המערכת. מבחינה מתמטית טען ד'אלמבר ש-

הכוחות הפועלים על גוף המאולץ להחליק על משטח. הכוח שהאילוץ מפעיל מסומן ב-C, וכוחות אחרים מסומנים ב-N. העתקה וירטואלית מסומנת ב-$\delta \mathbf {r}$ ובסופה הגוף עדיין מקיים את האילוץ כלומר ממוקם על המשטח.

$\sum _{i}\left(\mathbf {F} _{i}-{\dot {\mathbf {p} }}_{i}\right)\cdot \delta \mathbf {r} _{i}=0$

כאשר

$\mathbf {F} _{i}$	הם הכוחות המופעלים על הגוף ה-i במערכת,
$\mathbf {p} _{i}\scriptstyle$	הוא התנע של הגוף ה-i במערכת
$\delta \mathbf {r} _{i}$	הם ההעתקים הווירטואליים המצייתים לאילוצי המערכת,

תוצאה זו נובעת מיידית מחוקי ניוטון לפיהם לכל גוף מתקיים ${\dot {\mathbf {p} }}_{i}=\mathbf {F} _{i}$.

בצורה זו, עקרון ד'אלמבר לא מחדש הרבה ביחס לחוקי התנועה של ניוטון. היתרון הגדול של העיקרון מגיע כאשר מפרידים את הכוחות במערכת לכוחות המקושרים לאילוצים $\mathbf {C} _{i}$ ולכוחות רגילים $\mathbf {N} _{i}$. באופן די כללי, כוחות הנובעים מאילוצים פועלים במאונך לכיוון ההעתקות הווירטואליות ולכן הם לא מבצעים עבודה וירטואלית על המערכת. לפיכך עקרון ד'אלמבר יכול להיכתב בצורה:

$\sum _{i}\left(\mathbf {N} _{i}-{\dot {\mathbf {p} }}_{i}\right)\cdot \delta \mathbf {r} _{i}+\sum _{i}\mathbf {C} _{i}\cdot \delta \mathbf {r} _{i}=\sum _{i}\left(\mathbf {N} _{i}-{\dot {\mathbf {p} }}_{i}\right)\cdot \delta \mathbf {r} _{i}=0$

בצורה זו, עקרון ד'אלמבר מספק מידע על המערכת מבלי להשתמש במידע על כוחות האילוצים. כפי שהוסבר לעיל, מציאת הכוחות $\mathbf {C} _{i}$ היא בעיה כשלעצמה, כשאין לה דרך פתרון סדיר במכניקה ניוטונית. לכן, עקרונות מכניים שלא משתמשים בכוחות הללו הם צעד חשוב בפיתוח המכניקה הקלאסית.

קואורדינטות מוכללות, כוחות מוכללים ומשוואות התנועה

עקרון ד'אלמבר אמנם מסיר את הכוחות המאלצים מהתמונה, אך הם עדיין מופיעים כהגבלות על ההעתקים הווירטואליים - הווקטורים $\delta \mathbf {r} _{i}$ אינם בלתי תלויים. אם יש $m$ אילוצים על המערכת, וכל האילוצים על המערכת הם אילוצים הולונומים, כלומר ניתן לכתוב לכל אילוץ משוואה מהצורה $f(\mathbf {r} _{1},\mathbf {r} _{2},...,\mathbf {r} _{N},t)=0$, אז ניתן להציג סט חדש של קואורדינטות מוכללות, $\left\{q_{j}\right\}_{j=1}^{n}$ כאשר ($n=dN-m$ מספר דרגות החופש של המערכת ($d$ מספר הממדים בבעיה)). כך שמתקיים:

$\mathbf {r} _{i}=\mathbf {r} _{i}(q_{1},q_{2},...,q_{n},t)$

והמשתנים $\mathbf {q}$ הם בלתי תלויים. במצב כזה מתקיים $\delta \mathbf {r} _{i}=\sum _{j}{\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}\delta q_{j}$ כעת ניתן להגדיר את הכוחות המוכללים $Q_{j}=\sum _{i}\mathbf {N} _{i}\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}$ ומתקיים $\sum _{i}\mathbf {F} _{i}\cdot \delta \mathbf {r} _{i}=\sum _{i}\mathbf {N} _{i}\cdot \delta \mathbf {r} _{i}=\sum _{j}Q_{j}\delta q_{j}$. כעת ניתן לפתח את האיבר השני בעקרון ד'אלמבר ולהציגו באמצעות הקואורדינטות המוכללות ולקבל $\sum _{i}{\dot {\mathbf {p} }}_{i}\cdot \delta \mathbf {r} _{i}=\sum _{j}\left[{\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}\right]\delta q_{j}$ כאשר $T=\sum _{i}{\frac {1}{2}}m_{i}v_{i}^{2}$ האנרגיה הקינטית של המערכת. שימוש בשתי התוצאות הללו מניב עבור עקרון ד'אלמבר:

$\sum _{j}\left[{\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}-Q_{j}\right]\delta q_{j}=0$

אם כל האילוצים הם הולונמים, ונעשה שימוש ב-$n$ קואורדינטות מוכללות, אזי הקואורדינטות המוכללות בלתי תלויות. במצב כזה, השוויון הנל יכול להתקיים רק אם:

$\forall 1\leq j\leq n:{\frac {d}{dt}}{\frac {\partial T}{\partial {\dot {q}}_{j}}}-{\frac {\partial T}{\partial q_{j}}}=Q_{j}$

משוואות אלו מכונות משוואות לגראנז' או משוואות התנועה הכלליות. הן מקשרות בין הכוחות הרגילים במערכת לתנועת המערכת מבלי לפתור או להשתמש בכוחות המאלצים. האילוצים על המערכת מופיעים במשוואות הללו רק בבחירת סט של קואורדינטות מוכללות שמקיימות את האילוצים.

אם הכוחות הרגילים במערכת הם כוחות משמרים, כלומר קיים פוטנציאל סקלארי $V(\mathbf {r} _{1},...,\mathbf {r} _{N},t)$ כך ש-$\mathbf {N} _{i}=-\nabla _{i}V$ הרי שמתקיים $Q_{j}=-\sum _{i}\nabla _{i}V\cdot {\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}=-{\frac {\partial V}{\partial q_{j}}}$ ומכאן (נשים לב שבמצב זה ${\frac {\partial V}{\partial {\dot {q}}_{j}}}=0$)

$\forall 1\leq j\leq n:{\frac {d}{dt}}{\frac {\partial (T-V)}{\partial {\dot {q}}_{j}}}-{\frac {\partial (T-V)}{\partial q_{j}}}=0$

סט משוואות אלו ידוע בשם משוואות אוילר-לגראנז'.

משוואות אלו יכולות לשמש גם במצבים בהם הכוחות לא משמרים, אך קיים פוטנציאל מוכלל $V(\mathbf {q} ,{\dot {\mathbf {q} }},t)$ כך שמתקיים: $Q_{j}=-{\frac {\partial V}{\partial q_{j}}}+{\frac {d}{dt}}{\frac {\partial V}{\partial {\dot {q}}_{j}}}$. פוטנציאל כזה קיים לדוגמה עבור חלקיק בעל מטען $q$ הנע בשדה אלקטרומגנטי, ועבור $V(\mathbf {r} ,\mathbf {\dot {r}} ,t)=q\phi -q\mathbf {A} \cdot \mathbf {\dot {r}}$ כאשר $\phi$ הפוטנציאל החשמלי, ו-$\mathbf {A}$ הפוטנציאל הווקטורי.

הלגראנז'יאן ותכונותיו

ערך מורחב – לגראנז'יאן

את הפונקציה $L(\mathbf {q} ,{\dot {\mathbf {q} }},t)=T-V$ מגדירים כלגראנז'יאן של המערכת. הקואורדינטות $\mathbf {q}$ מתארות את המיקומים האפשריים של המערכת המקיימים את האילוצים על המערכת. המרחב אותו הן מתארות נקרא מרחב הקונפיגורציות. המהירויות ${\dot {\mathbf {q} }}$ מתארות משיקים למרחב הקונפיגורציות. בהינתן סט של קואורדינטות מוכללות הלגראנז'יאן מתאר את המערכת הפיזיקלית באופן מלא.

אינווריאנטיות תחת טרנספורמציות נקודה

מרחב הקונפיגורציות ניתן לתיאור על ידי קואורדינטות מוכללות שונות. טרנספורמציית נקודה היא החלפה בין מערכת קואורדינטות אחת לאחרת. טרנספורמציה כזו יכולה להיכתב באמצעות משוואות $q_{j}=q_{j}(s_{1},s_{2},...s_{n},t)$. משוואות אוילר-לגראנז' מתקיימות עבור אותה פונקציה לגראנז'יאן כפי שהיא נכתבת בקואורדינטות החדשות, כלומר הלגראנז'יאן הוא אינווריאנטי תחת שינוי הקוארדינטות. הוכחה:

${\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {s}}_{j}}}={\frac {d}{dt}}\left[\sum _{k}{\frac {\partial L}{\partial q_{k}}}{\frac {\partial q_{k}}{\partial {\dot {s}}_{j}}}+{\frac {\partial L}{\partial {\dot {q}}_{k}}}{\frac {\partial {\dot {q}}_{k}}{\partial {\dot {s}}_{j}}}\right]={\frac {d}{dt}}\sum _{k}{\frac {\partial L}{\partial {\dot {q}}_{k}}}{\frac {\partial q_{k}}{\partial s_{j}}}=\sum _{k}{\frac {\partial L}{\partial {\dot {q}}_{k}}}{\frac {\partial {\dot {q}}_{k}}{\partial s_{j}}}+{\frac {\partial L}{\partial q_{k}}}{\frac {\partial q_{k}}{\partial s_{j}}}={\frac {\partial L}{\partial s_{j}}}$

פונקציית האנרגיה

פונקציית האנרגיה של המערכת מוגדרת על ידי $E(\mathbf {q} ,{\dot {\mathbf {q} }},t)=\sum _{j}{\frac {\partial L}{\partial {\dot {q}}_{j}}}{\dot {q}}_{j}-L$, נתבונן בנגזרת של פונקציית האנרגיה לפי הזמן:

${\frac {dE}{dt}}=\sum _{j}{\dot {q}}_{j}{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}+{\frac {\partial L}{\partial {\dot {q}}_{j}}}{\ddot {q}}_{j}-{\dot {q}}_{j}{\frac {\partial L}{\partial q_{j}}}-{\ddot {q}}_{j}{\frac {\partial L}{\partial {\dot {q}}_{j}}}-{\frac {\partial L}{\partial t}}=-{\frac {\partial L}{\partial t}}$

לכן אם הלגראנז'יאן לא תלוי ישירות בזמן, פונקציית האנרגיה של המערכת נשמרת.

אם הפוטנציאל לא תלוי במהירויות (כלומר הכוחות הם כוחות משמרים) והלגראנז'יאן לא תלוי בזמן מתקיים $\sum _{j}{\frac {\partial L}{\partial {\dot {q}}_{j}}}{\dot {q}}_{j}=\sum _{j}{\frac {\partial T}{\partial {\dot {q}}_{j}}}{\dot {q}}_{j}=2T$ ולכן פונקציית האנרגיה מקיימת $E=T+V$ והיא מתלכדת עם האנרגיה של המערכת. באופן כללי פונקציית האנרגיה אינה סכום של האנרגיה הפוטנציאלית והפוטנציאל המוכלל.

דמיות מכנית

אם האנרגיה הפוטנציאלית לא תלויה במהירויות ובזמן, והיא פונקציה הומוגנית של הקואורדינטות, כלומר מתקיים $V(\alpha \mathbf {r} _{1},\alpha \mathbf {r} _{2},...,\alpha \mathbf {r} _{n})=\alpha ^{k}V(\mathbf {r} _{1},\mathbf {r} _{2},...,\mathbf {r} _{n})$, האנרגיה הקינטית היא פונקציה הומוגנית מסדר שני של המהירויות $T(\alpha \mathbf {v} _{1},\alpha \mathbf {v} _{2},...,\alpha \mathbf {v} _{n})=\alpha ^{2}T(\mathbf {v} _{1},\mathbf {v} _{2},...,\mathbf {v} _{n})$. $\mathbf {r} \to \alpha \mathbf {r} ;t\to \alpha ^{1-k/2}t$ גורמת ל-$L\to \alpha ^{k}L$, הכפלה בקבוע של הלגראנז'יאן לא משנה את משוואות התנועה, ולכן לא משנה את צורת המסלולים. המשמעות היא שזמן המחזור של מערכת גדולה יותר בפקטור $\alpha$ יהיה ארוך יותר בפקטור של $\alpha ^{1-k/2}$. לדוגמה, בתנודות קטנות ליד מינימום של פוטנציאל $k=2$ וזמן המחזור לא תלוי באמפליטודה התנודה. בנפילה חופשית $k=1$ וזמן הנפילה פרופורציונלי לשורש הגובה של הנפילה. בחוק הכבידה האוניברסלי של ניוטון $k=-1$ וזמן התנועה בריבוע פרופורציונלי לאמפליטודת התנועה בשלישית - זהו אחד מחוקי קפלר.

אילוצים כלליים וכופלי לגראנז'

לא כל סט אילוץ על מצב המערכת הוא אילוץ הולונומי. לדוגמה: כדור המתגלגל (ללא החלקה) על פני מישור, מקיים אילוץ לפי המהירות הזוויתית של הגלגול מקושרת למרחק אותו הכדור עובר, עם זאת, החופש של הכדור להתגלגל בכיוונים שונים גורמת לכך שהזווית של הכדור לא מקושרת למיקומו. במקרים כאלה יכול להיות אילוץ לא הולונומי מהצורה $f(\mathbf {q} ,{\dot {\mathbf {q} }},t)=0$ כאשר $\mathbf {q}$ הוא סט קואורדינטות מוכללות המתאר מרחב המכיל את מרחב הקונפיגורציות. במקרה הזה, הקואורדינטות המתארות את מרחב הקונפיגורציות יהיו תלויות אחת בשנייה. בפיתוח לעיל, עקרון ד'אלמבר גרר את משוואות אוילר-לגראנז' בעקבות ההנחה שהקואורדינטות בלתי תלויות. כדי לקבל את משוואות אוילר-לגראנז' כאשר הקואורדינטות תלויות ניתן להשתמש בכופלי לגראנז'. אם יש $m$ אילוצים על המערכת, ניתן להוסיף ללגראנז'יאן את הביטוי ${\tilde {L}}=L+\sum _{\alpha =1}^{m}\lambda _{\alpha }(t)f_{\alpha }(\mathbf {q} ,{\dot {\mathbf {q} }},t)$ וכעת להתייחס לקואורדינטות כבלתי תלויות כך שמתקבלות $m$ משוואות אילוצים כאשר מתייחסים ל-$\lambda _{\alpha }$ כמשתנה:

$\forall 1\leq \alpha \leq m:f_{\alpha }(\mathbf {q} ,{\dot {\mathbf {q} }},t)=0$

וכן מתקבל הסט הבא של $n+m$ ($n$ מספר דרגות החופש של המערכת) משוואות אוילר-לגראנז':

$\forall 1\leq j\leq n+m:{\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {q}}_{j}}}-{\frac {\partial L}{\partial q_{j}}}=\sum _{\alpha =1}^{m}\left[\lambda _{\alpha }\left[{\frac {\partial f_{\alpha }}{\partial q_{j}}}-{\frac {d}{dt}}{\frac {\partial f_{\alpha }}{\partial {\dot {q}}_{j}}}\right]-{\frac {d\lambda _{\alpha }}{dt}}{\frac {\partial f_{\alpha }}{\partial {\dot {q}}_{j}}}\right]=\sum _{\alpha =1}^{m}C_{\alpha j}$

צד שמאל של המשוואות הן הכוחות כתוצאה מהחלקיקים במערכת ומהאילוצים שהוכנסו בבחירת הקואורדינטות הכלליות, וצד ימין כולל את הכוחות כתוצאה מהאילוצים שלא הוכנסו בבחירת הקואורדינטות. המשוואה נותנת ביטוי לכוחות הללו, התלוי בגדלים של $\lambda _{\alpha }$. בכך, השימוש בכופלי לגראנז' מאפשר לחשב את הכוח שכל אילוץ, הולונומי או לא הולונומי, מפעיל על המערכת. זהו עוד יתרון של המכניקה הלגראנז'ית, שכן במכניקה הניוטונית, למעט במקרים פשוטים, חישוב הכוחות הללו אפשרי רק אחרי פתרון מלא של הבעיה. את שיטת כופלי לגראנז' ניתן להפעיל גם על אילוצים הולונומיים, אם רוצים למצוא את הכוחות שהאילוצים מפעילים, או שקשה למצוא סט מלא של קואורדינטות מוכללות לתאר את המערכת.

עקרון המילטון

הדגמה של עקרון המילטון במערכת דו־ממדית. המסלול בו המערכת תנוע הוא מסלול בו שינויים קטנים של המסלול (המצוינים ב-$\delta \mathbf {q}$) לא ישנו את הערך של הפעולה.

הפיתוח שהוצג עברו המכניקה הלגראנז'ית התבסס על עקרון ד'אלמבר. עקרון ד'אלמבר הוא עקרון דיפרנציאלי - הוא מסתכל על נקודת זמן ספציפית בתנועה, וקובע מה יהיה מצב המערכת בנקודת זמן קצרה אחריה. את המכניקה הלגראנז'ית ניתן לפתח באופן שקול מעקרון אינטגרלי, המסתכל על המסלול בכללותו, וקובע שהמסלול בין שתי נקודות חייב לקבל ערך סטציונרי עבור איזושהי פונקציונל של פונקציה $L$. באמצעות חשבון וריאציות אפשר להראות שהפונקציה $L$ חייבת לקיים את משוואות אוילר-לגראנז', ולכן הפונקציה $L$ במכניקה האנליטית היא פונקציית הלגראנז'יאן כפי שהוגדרה לעיל.

ניסוח מתמטי

עקרון המילטון קובע שבהינתן מערכת פיזיקלית $(M,L)$ שתי נקודות $[t_{0},t_{1}]\subseteq \mathbb {R} _{t}$ ושתי נקודות $\mathbf {q} _{0},\mathbf {q} _{1}\in M$, כך שבזמן $t_{0}$ המערכת נמצאת בנקודה $\mathbf {q} _{0}$ ובזמן $t_{1}$ ב-$\mathbf {q} _{1}$. המערכת תנוע במרחב הקונפיגורציות במסלול $\gamma :[t_{0},t_{1}]\to M$ כך שהפעולה המוגדרת על ידי האינטגרל $S[\gamma ]=\int _{t_{0}}^{t_{1}}L(\gamma (t),{\dot {\gamma }}(t),t)\ dt$ תהיה סטציונרית, כלומר תקיים $\delta S=0$.

אי ייחודיות

מעקרון המילטון קל לראות שהלגראנז'יאן המתאר את המערכת אינו ייחודי. מאחר שאם הפונקציה $L$ מתארת את המערכת, כל פונקציה מהצורה ${\tilde {L}}=aL+{\frac {df}{dt}}$ (כאשר $a\in \mathbb {R}$ קבוע, ו-$f:TM\times \mathbb {R} _{t}\to \mathbb {R}$ פונקציה חלקה) נותנת אותם מסלולים סטציונרים שכן $\delta {\tilde {S}}=a\delta {S}+\delta \int _{t_{0}}^{t_{1}}{\frac {df}{dt}}dt=a\delta {S}+\delta \left[f(t_{1})-f(t_{0})\right]=a\delta S$.

היתרונות בשימוש בעקרון המילטון

עקרון המילטון, עקרון ד'אלמבר ומשוואות התנועה של אוילר-לגראנז' הם כולם ניסוחים שקולים של אותם חוקי תנועה. לעקרון המילטון יש מספר יתרונות על פני הניסוחים האחרים. ראשית, אי הייחודיות של הלגראנז'יאן מפותחת באופן טריוויאלי מהעיקרון, בעוד בניסוחים האחרים היא יוצאת מפיתוח ארוך. בנוסף, עקרון המילטון לא דורש שימוש בקואורדינטות, ולכן האינווריאנטיות של הלגראנז'יאן מוטמעת בעקרון ואינה תוצאה של חישוב. חשוב מכך, את עקרון המילטון קל יותר להרחיב לתחומים אחרים של הפיזיקה - עקרון פרמה הוא הרחבה כזו לתחום של אופטיקה גאומטרית; החלפה של $dt$ באינטרוול היחסותי $ds$ תניב את משוואות התנועה של חלקיק בשדה אלקטרומגנטי בתורת היחסות הפרטית; תורת שדות קלאסית מנוסחת על ידי עקרון המילטון כשמרחב הקונפיגורציות הוא מממד אינסופי, גם משוואות מקסוול לשדה האלקטרומגנטי נובעות מעקרון המילטון עם בחירה מושכלת של הלגראנז'יאן.

ראו גם

• מכניקה קלאסית
• חוקי התנועה של ניוטון
• מכניקה אנליטית
• לגראנז'יאן
• המילטוניאן
• משוואת המילטון-יעקובי
• עקרון המילטון
• עקרון ד'אלמבר
• עקרון האילוץ המינימלי של גאוס
• אילוצים הולונומים
• קואורדינטות מוכללות
• חשבון וריאציות

לקריאה נוספת

• L.D. Landau and E.M. Lifshitz. (1960). Mechanics. Pergamon Press
• H. Goldstein. (1980). Classical Mechanics (2nd ed.). Addison–Wesley
• .Hand & Finch. (1998) Analytical Mechanics (1st Edition) Cambridge University Press