פוטנציאל חשמלי

באלקטרוסטטיקה, הפוטנציאל החשמלי (מסומן לרוב ב-$\ \phi$ או ב-$\varphi$) הוא האנרגיה הפוטנציאלית החשמלית של מטען בוחן בגודל 1 קולון.

בדומה לכל אנרגיה פוטנציאלית, הפוטנציאל החשמלי נקבע רק עד כדי קבוע התלוי בנקודת יחוס. הגודל בעל המשמעות הפיזיקלית אינו הפוטנציאל עצמו אלא הפרשי ערכי הפוטנציאל בנקודות שונות, המכונה מתח חשמלי. גודל זה הוא העבודה שיש לבצע כנגד הכוח החשמלי על מנת להעביר מטען בוחן בין הנקודות. מקובל לקבוע את הפוטנציאל כך שהוא מתאפס ב"אינסוף" (במרחק גדול מן המערכת הפיזיקלית) ובמקרה זה הפוטנציאל החשמלי בנקודה כלשהי הוא העבודה שיש לבצע על מנת להביא לנקודה זו מטען בוחן מהאינסוף.

הפוטנציאל החשמלי הוא גודל סקלרי הנמדד ביחידות של וולט במערכת היחידות SI ובסטטוולט במערכת היחידות CGS.

הגדרה מתמטית

השדה החשמלי האלקטרוסטטי $\vec E$ הינו שדה משמר (מקיים $\vec \nabla \times \vec E = 0$). מכאן נובע קיומה של פונקציה סקלרית $\ \phi$ מתוכה ניתן לגזור את השדה החשמלי על ידי $\vec E = -\vec \nabla \phi$. פונקציה זו היא הפוטנציאל החשמלי.

את הפוטנציאל החשמלי ניתן לחשב על ידי קביעת ערכו באופן שרירותי בנקודה מסוימת $\phi(\vec r_0)=0$, ולאחר מכן ערכו בכל נקודה אחרת יחושב על ידי אינטגרציה של השדה החשמלי:

$\phi(\vec r) = -\int \vec E \cdot d\vec r$

כאשר האינטגרציה מתבצעת על גבי מסילה כלשהי המחברת בין הנקודות $\vec r_0,\vec r$.

דוגמאות

שדה ופוטנציאל של דיפול חשמלי. החצים מתארים את השדה החשמלי והקווים הרציפים הם קווים שווי פוטנציאל (מחברים נקודות בעלות אותו פוטנציאל)

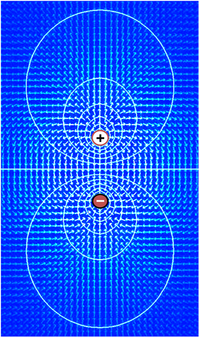
• הפוטנציאל החשמלי סביב מטען נקודתי $\ q$ הוא $\frac{kq}{r}$, כאשר $\ r$ הוא המרחק מן המטען.
• הפוטנציאל החשמלי שיוצר תיל "אינסופי" טעון בצפיפות מטען $\ \lambda$ ליחידת אורך הוא $\ -2k\lambda \ln \left(\frac{r}{r_0}\right)$, כאשר $\ r$ הוא המרחק מהתיל ו-$\ r_0$ נקודת יחוס שרירותית בה הפוטנציאל מתאפס.

משמעות פיזיקלית

הפוטנציאל החשמלי הוא בעצם האנרגיה הפוטנציאלית של מטען בוחן בגודל 1 (היחס בין פוטנציאל ואנרגיה, דומה ליחס בין השדה החשמלי לכוח החשמלי). כיוון שיש חופש בבחירת נקודת יחוס בה הפוטנציאל מתאפס, רק להפרשי פוטנציאל בין נקודות שונות יש משמעות פיזיקלית. הפרש זה, הקרוי מתח, הוא העבודה שיש להשקיע כנגד השדה החשמלי על מנת להעביר מטען בוחן בין שתי הנקודות. מקובל לקבוע את הפוטנציאל כך שהוא מתאפס ב"אינסוף" (במרחק גדול מן המערכת הפיזיקלית) ובמקרה זה הפוטנציאל החשמלי בנקודה כלשהי הוא העבודה שיש לבצע על מנת להביא לנקודה זו מטען בוחן מהאינסוף.

צורת הפוטנציאל קובעת את האופן בו ינועו מטענים. סימן המינוס בהגדרת הפוטנציאל גורם לכך שמטענים חיובים ינועו מפוטנציאל גבוה לפוטנציאל נמוך ואילו מטענים שליליים ינועו מפוטנציאל נמוך לפוטנציאל גבוה. באופן מדויק יותר, הכוח שיפעל על המטענים הוא בכיוון גרדיאנט הפוטנציאל עבור מטען שלילי ובכיוון הפוך לכיוון הגרדיאנט עבור מטען חיובי $(\vec F = q \vec E= -q\vec \nabla \phi)$.

הפוטנציאל החשמלי ומשוואת פואסון

מחוק גאוס נובע כי הפוטנציאל החשמלי מקיים את משוואת פואסון:

$\nabla^2 \phi = -4\pi k \rho$.

כאשר $\ \rho$ צפיפות המטען במרחב ו- $\ k$ קבוע קולון.

בהינתן התפלגות מטען כלשהי $\ \rho$, פתרון המשוואה עבור הפוטנציאל הוא:

$\phi (\vec r) = k \int \frac{\rho(\vec r^')}{|\vec r - \vec r^'|} d\vec r^'$

הפוטנציאל החשמלי באלקטרומגנטיות

בנוכחות שדה מגנטי משתנה בזמן, השדה החשמלי אינו שדה משמר ומתקיים: $\vec \nabla \times \vec E = - \frac{\partial \vec B}{\partial t}$. לכן לא ניתן להגדיר פוטנציאל חשמלי באופן דומה למקרה האלקטרוסטטי ממנו ניתן לגזור את השדה החשמלי על ידי $\vec E = -\vec \nabla \phi$. למרות זאת, ניתן במקרה זה לגזור את השדה החשמלי מתוך הפוטנציאל הווקטורי $\vec A$ והכללה כלשהי של הפוטנציאל החשמלי (פוטנציאל סקלרי $\ \phi$).

למרות שהשדה החשמלי אינו משמר, השדה $\vec E + \frac{\partial \vec A}{\partial t}$ כן משמר וניתן לגזור אותו מתוך פוטנציאל סקלרי: $\vec E + \frac{\partial \vec A}{\partial t}= -\vec \nabla \phi$.

כלומר במקרה זה, אין לפוטנציאל החשמלי משמעות של אנרגיה, אך ניתן להיעזר בו ובפוטנציאל הווקטורי על מנת לקבל את השדה החשמלי:

$\vec E =- \frac{\partial \vec A}{\partial t} -\vec \nabla \phi$

חופש כיול

כיוון שהשדה החשמלי נגזר מתוך שילוב של הפוטנציאל הווקטורי והסקלרי, חופש הכיול של הפוטנציאל הווקטורי גורר גם חופש כיול לפוטנציאל הסקלרי. כלומר הפוטנציאלים $\vec A+\vec \nabla \Lambda , \phi -\frac{\partial \Lambda}{\partial t}$ (עבור $\ \Lambda$ כלשהי) מתארים אותם שדות חשמליים ומגנטיים כמו $\vec A, \phi$.

4-וקטור הפוטנציאל

בניסוח יחסותי של האלקטרומגנטיות, מאוגדים הפוטנציאל הסקלרי והווקטורי ל4-וקטור $A^{\mu} =( \phi, \vec A )$. 4-וקטור הפוטנציאל משמש להגדרת טנזור השדה האלקטרומגנטי.

ראו גם

• מתח חשמלי
• פוטנציאל וקטורי
• שדה חשמלי
• הארקה