אלמנטים סופיים

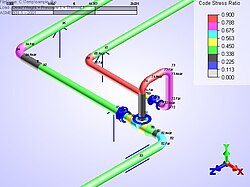

אנליזה בשיטת האלמנטים הסופיים (Finite Element Analysis) ובקיצור (FEA), היא טכניקה לחישוב נומרי של משוואות דיפרנציאליות המתארות בעיות של שדות כמו שדה מאמצים ושדה של זרימה.
אלמנטים סופיים היא שיטה מקובלת ונפוצה בפתרון של בעיות הנדסיות רבות בעזרת מחשב תוך שימוש בתוכנות מחשב מיוחדות הפועלות בשיטת האלמנטים הסופיים (באנגלית: Finite Element Method ובקיצור FEM).
הרעיון[עריכת קוד מקור | עריכה]
הרעיון הראשון לתאר את גוף המוצק כמספר אלמנטים עם מידות סופיות שייך לפואסון (M.Poisson,1829). שיטת האלמנטים הסופיים פותחה לראשונה בשנת 1943 על ידי ריצ'רד קוראנט (Richard Courant) שהשתמש בשיטת ריץ (Ritz method) שהיא שיטה נומרית, כדי לקבל פתרון מקורב למערכת רוטטת. בשנת 1956 התפרסם מאמר מרחיב על ידי M. J. Turner, R. W. Clough, H. C. Martin, and L. J. Topp אשר התייחס לשיטת האלמנטים הסופיים בנושא קשיחות ותזוזות של מבנים מורכבים. במכניקת המבנים הפיתוח של המשוואות לפתרון באלמנטים סופיים מבוסס על עקרונות שימור האנרגיה וכלל פוטנציאל האנרגיה המינימלי.
בשנת 1973 פרסמו Strang and Fix ספר בשם "אנליזה של שיטת האלמנטים הסופיים" (An Analysis of The Finite Element Method) שהעמיד את השיטה על בסיס מתמטי מוצק והפך אותה לשיטה נומרית מוכרת שמרבים להשתמש בה בהנדסה. פרופסור רוברט קוק מאוניברסיטת ויסקונסין–מדיסון כתב בשנת 1974 ספר לימוד בשם Concepts and Applications of Finite Element Analysis, שהפך למקור מידע בנושא האלמנטים הסופיים כולל רקע מתמטי ורקע היסטורי.
עקרון הפעולה[עריכת קוד מקור | עריכה]
בשיטת האלמנטים הסופיים האובייקט מתואר על ידי מודל גאומטרי המחולק לאלמנטים סופיים. המשוואות נכתבות לכל אלמנט לפי הבעיה הפיזיקלית המתוארת על ידי המודל וכל מערכות המשוואות של המודל המיוצגות על ידי המשוואות של האלמנטים. מערכת המשוואות הזו נפתרת בטכניקות של אלגברה ליניארית או בשיטות נומריות לא ליניאריות לפי אופי המשוואות. דיוק הפתרון של השיטה משתפר כאשר האלמנטים קטנים יותר או כאשר האלמנט מורכב יותר על ידי תוספת נקודות וכאשר הצורה של האלמנטים די אחידה.
מרבים להשתמש בשיטת האלמנטים הסופיים לחישוב מאמצים ותזוזות של מבנים ושל מערכות מכניות וכן בפתרון של בעיות מורכבות במעבר חום, זרימה, אלקטרומגנטיות ועוד. דוגמה למערכת משוואות ליניאריות לפתרון בעיית חישוב של גוף אלסטי בהשפעת כוחות חיצוניים:
- המשוואה הווקטורית היא {F} = [K] * {X}, כאשר:
- {F} - וקטור כוחות.
- {X} - וקטור תזוזות.
- [K] - מטריצת קשיחות
שימוש[עריכת קוד מקור | עריכה]
השימוש המעשי באלמנטים הסופיים החל בתעשייה האווירית בחישוב מבני מטוסים, בתעשיית הימית בחישוב מבני אוניות, בחישוב של מבנים מורכבים, בחישוב צנרת לחץ חמה בתחנות כוח ובכורים גרעיניים ובחישובים הדרושים בתעשיית הרכב. היום השימוש בשיטה נפוץ ומגוון בשטחים שונים של הפיזיקה ושל ההנדסה כולל הנדסת קרקע לדוגמה והנדסה ביו רפואית כמו חישובי חוזק השלד של בני אדם. מצד אחד יש היצע של תוכנות אלמנטים סופיים כלליות ומצד שני תוכנות ייעודיות המותאמות למשימות חישוב ספציפיות.
ההתפתחות של התוכנות לאלמנטים סופיים ושל המחשבים מאפשרים חישובים מורכבים של תהליכים כמו התנגשות מכוניות. החישוב מעגלי כאשר מעגל החישוב הקודם מגדיר את תנאי השפה של החישוב הבא. משך החישוב עדיין לא נעשה בזמן אמת אבל בסוף התהליך ניתן להציג סרטון הדמיה של האירוע כאילו הוא בוצע מול עינינו. השימוש היום יומי איננו דורש ידע בפיתוח המשוואות הדיפרנציאליות והפתרון שלהם, אלא הכרה טובה של הנושא, בניית מודל טוב המתאים למציאות שייתן תוצאות קרובות למציאות, קביעת תנאי שפה וחלוקה טובה לאלמנטים.
לקריאה נוספת[עריכת קוד מקור | עריכה]
- Finite Element Modeling by Constantine C. Spyrakos West Virginia University Press, 1994. ISBN 0964193914
- Finite Element Analysis by John R. Brauer Marcel Mekker Inc. ISBN 0824789547
- O.C. Zienkiewicz, R.L. Taylor & J.Z. Zhu, The Finite Element Method: Its Basis & Fundamentals, ISBN 0750663200
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- מבוא לשיטת האלמנטים הסופיים, באתר קומסול מולטיפיזיקס
- היסטורית אנליזת מבנים בשימוש מטריצות
 שיטת אלמנטים סופית, דף שער בספרייה הלאומית
שיטת אלמנטים סופית, דף שער בספרייה הלאומית- אלמנטים סופיים, באתר MathWorld (באנגלית)
