מאמץ (הנדסה)

מאמץ (או לחץ) בהנדסת חומרים הוא כוח בתוך חומר ליחידת שטח. חישוב ומדידה של מאמץ עומדים במרכז תורת החוזק. בהנדסת מכונות והנדסה אזרחית מודדים ומחשבים מאמץ בחומרים, על מנת לקבוע את תפקודה של מערכת תחת עומסים קיצוניים, כלומר לקבוע האם החומרים יעמדו בעומס.
מאמץ שיורי בתוך חומר הוא מאמץ שקיים גם בלי הפעלת כוח, והוא נגרם בדרך כלל כתוצאה מטיפולים קודמים שעבר החומר, תרמיים ומכניים. מאמץ שיורי יכול להחליש את החומר ולעוות את צורתו, ולעיתים גם לסדוק או לשבור את החומר.
הגדרת המאמץ[עריכת קוד מקור | עריכה]
מאמץ נמדד תמיד ביחידת כוח ליחידת שטח, בדרך כלל בניוטון/קילוניוטון למילימטר/סנטימטר/מטר מרובע או ביחידות פסקל/מגה-פסקל.
מאמץ המתיחה והלחיצה למשל הוא כאשר: - ערך המאמץ, - ערך הכוח הפועל, - שטח חתך הגוף.
בצורה דומה מוגדר מאמץ הגזירה
ניתן לראות שככל שהכוח הפועל על הגוף גדל, גדל גם המאמץ ואילו ככל ששטח החתך גדל, המאמץ קטן. בכפיפה, פיתול וקריסה למשל, הנוסחאות מורכבות יותר.
העיקרון של קושי[עריכת קוד מקור | עריכה]
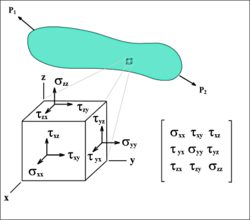
עיקרון שווי המשקל הפנימי של קושי קובע שכאשר חותכים גוף על ידי מעטפת סגורה, הכוחות הפועלים על המעטפת הזו נמצאים בשווי משקל עם הכוחות הפועלים על המעטפת של שארית הגוף. כך אנו יכולים לבחון את המאמץ הפועל על קובייה קטנה בתוך הגוף עצמו. בקובייה תלת־ממדית על פני פאת הקובייה, פועלים שני כוחות גזירה במישור פאת הקובייה וכח אחד ניצב לפאה. במצב המאמצים התלת־ממדי, טנזור מאמצים מתאר את המאמצים הפועלים על הקובייה.
עקומת מאמץ-מעוות[עריכת קוד מקור | עריכה]
 ערך מורחב – עקומת מאמץ-מעוות
ערך מורחב – עקומת מאמץ-מעוות


בעת הפעלת כוח על קורה מידותיה משתנות (גם אם לפעמים במידה קטנה, אשר קשה לראותה בעין). שינוי זה במידות הקורה נקרא מעוות.
העיבור (strain)[עריכת קוד מקור | עריכה]
אם נחלק את גודל השינוי של המידה החדשה של הקורה (בדרך כלל, מידת האורך) במידתה המקורית, נקבל גודל חדש הוא המעוות היחסי הנקרא בעברית "עיבור" (strain). עקומת מאמץ-מעוות היא העקומה הנוצרת משרטוט המאמץ הפועל בדגם עבור כל ערך של עיבור. צורתה הכללית של דיאגרמת מאמץ-מעוות היא ליניארית בתחילתה, באזור בו מתקיים חוק הוק. תחום זה נקרא "התחום האלסטי". עיבור בתחום האלסטי הוא הפיך, כלומר עם הסרת העומס תחזור הגאומטריה של הקורה לקדמותה, ללא שיגרם לה נזק משמעותי (כמו קפיץ למשל).
לאחר הקטע הליניארי משתנה צורת הגרף ונהיית מורכבת יותר. תחום זה נקרא "התחום הפלסטי". עיבור בתחום הפלסטי הוא לא הפיך, כלומר גם כאשר יוסר העומס, הגוף לא יחזור לגודלו המקורי. רצוי שחומר הנדסי הנמצא במערכת עובדת יעבור רק עיבורים אלסטיים, שכן עבודה מעבר לגבול הכניעה גורמת לשינוי מידות החלק, ולאחר מכן לשבר בחומר. הנקודה העליונה בגרף נקראת נקודת הכניעה (או גבול הכניעה), ומשמעותה שמכאן ואילך אפילו מאמץ הנמוך מן הנוכחי יגדיל את המעוות (אשר לא ניתן היה להיות מושג בכוח כזה עד שהחומר הגיע לנקודת הכניעה). נקודת הכניעה קרובה לנקודת השבר, בה החומר נהרס.
בהנדסה[עריכת קוד מקור | עריכה]
חישובי מאמצים מאפשרים לחשב גדלים נדרשים של גופים כך שלא ייכשלו מבחינת חוזק. בתכנון גוף שידוע הכוח אשר אותו עליו לשאת, ניתן למצוא מהו המאמץ אשר ייווצר בו עבור מידה מסוימת של שטח חתך שתקבע עבורו. כיוון שעבור מרבית החומרים השימושיים בתעשייה ידועים ערכי המאמצים המותרים, ניתן (לאחר בחירת חומר הקורה) לחשב את מידותיה המינימליות הדרושות כך שהמאמץ בה לא יעבור את המאמץ המותר. אם ידוע הכוח הפועל ומשיקולי מיקום מוכתב גם שטח החתך של הקורה, ניתן לחפש חומר שיתאים לאלמנט המתוכנן שהמאמץ המותר שלו גבוה מהמאמץ שייווצר.
מקדם ביטחון[עריכת קוד מקור | עריכה]
לרוב לא עובדים בהנדסה בכל הטווח הליניארי של עקומת מאמץ-מעוות. עבודת הקורה המותרת היא רק בחלקו התחתון של החלק הליניארי. כדי להבטיח עבודה רק בתחום זה, לא מתייחסים בעת החישוב לגבול הכניעה, אלא מחלקים את הערך במקדם ביטחון, כדי לקבל את הערך של המאמץ המותר. ככל שמקדם הביטחון גדול יותר קטן הסיכוי לכשל, אך דבר זה גורר גאומטריה גדולה ומסורבלת יותר, או בחירת חומרים חזקים ויקרים יותר.
קביעת מקדם ביטחון נעשית כפשרה חישובית בין ההסתברות לכשל לבין תכן לא מופרז. ערכו של מקדם הביטחון משתנה מאוד מענף לענף וממידת הבטיחות הנדרשת, ובדרך כלל נמצא בתחום של 5 - 1.5.
סוגי מאמצים[עריכת קוד מקור | עריכה]
קיימים 3 סוגים של מאמצים בתוך חומר: מתיחה (שאיפה של חלקיקים להתרחק אחד מהשני), לחיצה (שאיפה של חלקיקים להתקרב אחד לשני) וגזירה (שאיפה של חלקיקים להיפרד זה מזה על המישור הניצב לקו המקשר ביניהם). שאר המאמצים הם מקרים פרטיים של מאמצים אלו או שילוב של מאמצים אלה.
- מאמץ מתיחה - מאמץ הנגרם עקב הפעלת זוג כוחות בכיוונים הפוכים כאשר שניהם פועלים בציר הקורה. הכוחות מנסים להאריך את הקורה.
- מאמץ לחיצה - במאמץ זה פועלים זוג כוחות על בכיוונים הפוך על ציר הקורה, אך הפעם הם מנסים לקצר אותה.
- מאמץ כפיפה - על הקורה פועלים עומסים הגורמים לה להתכופף בהשפעת מומנט כפיפה, חלק אחד של הקורה יהיה לחוץ וחלק אחר יהיה מתוח.
- מאמץ גזירה - זהו מקרה פרטי של כפיפה כאשר זוג הכוחות פועלים קרוב מאוד זה לזה.
- מאמץ פיתול - מאמץ הנגרם עקב זוג מומנטים בכיוונים הפוכים סביב ציר הקורה.
- מאמץ קריסה - מאמץ שנתגלה מאוחר ביחס למאמצים האחרים. מקרה פרטי של לחיצה. מתרחש כאשר הקורה גבוהה ודקה.
ראו גם[עריכת קוד מקור | עריכה]
לקריאה נוספת[עריכת קוד מקור | עריכה]
- Timoshenko S.P, Strength of Materials, 3rd edition, Krieger Publishing Company, 1976. ISBN 0-8827-5420-3
- Sybil P. Parker Editor in Chieh. McGraw-Hill Encyclopedia of Engineering, McGraw Hill Book Company, 1983, ISBN 0-0704-5486-8
- S.P. Timoshenkoo & J.N. Goodier Theory of Elasticity, 3rd edition, International Student Edition, McGraw-Hill, 1970.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- דוגמה לעקומת מאמץ-מעוות
- מאמץ ומעוות: מונחים ורעיונות בסיסיים (באנגלית)
- היחס בין מאמץ לבין מעוות (באנגלית)
- אלסטיות (באנגלית)
- מאמץ, באתר אנציקלופדיה בריטניקה (באנגלית)
| מאמץ (הנדסה) | ||
|---|---|---|
| מאמצים | מאמץ • מאמץ גזירה • מאמץ כפיפה • מאמץ לחיצה • מאמץ מתיחה • מאמץ פיתול • מאמץ קריסה • עייפות החומר | |
| נושאי עזר | מומנט כפיפה • מומנט כוח • אלסטיות • מעוות • חוק הוק • עקומת מאמץ-מעוות • כניעה (הנדסה) | |
| מודולי האלסטיות | מודול האלסטיות • מודול הגזירה • מקדם פואסון • קבועי לאמה • מודול הנפח | |
| שטחים ונפחים | שטח • מומנט התמד • מומנט ההתמד של השטח • מומנט התמד פולרי של השטח • משפט שטיינר-הויגנס • טנזור התמד • טבלת טנזורי התמד • מומנט ראשון של שטח | |
| נושאים משלימים | חוזק חומרים • טנזור מאמצים • מאמצים ראשיים • מעגל מור • היפותזות חוזק • שיטות אנרגיה • חוקי קסטיליאנו | |





