ניסוי שני הסדקים
יש לערוך ערך זה. הסיבה היא: הערך מתייחס לניסויים שונים בערבוביה, וכך מבלבל את הקורא.
| ||
| יש לערוך ערך זה. הסיבה היא: הערך מתייחס לניסויים שונים בערבוביה, וכך מבלבל את הקורא. | |
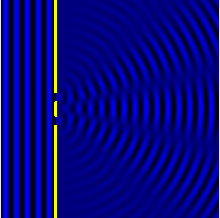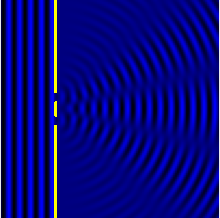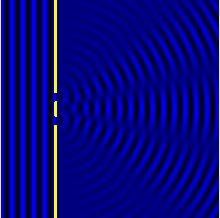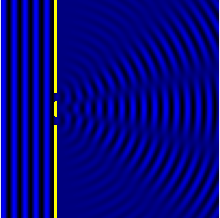
ניסוי שני הסדקים (מוכר גם בתור ניסוי יאנג) הוא ניסוי שנועד להבחין האם קרינה מסוג מסוים, מתפשטת כגל או כשטף של חלקיקים. הניסוי מוכיח שאור וחומר יכולים להראות גם תכונות של חלקיקים וגם של גל (תופעה הנקראת דואליות גל-חלקיק) והוא מהווה הוכחה לטבע ההסתברותי של מכניקת הקוונטים. רעיון הניסוי הוא שגלים, בשונה מחלקיקים, מחזקים או מחלישים זה את זה בהתאם למופע בו הם נפגשים.
הניסוי הראשון מסוג זה נערך על ידי הפיזיקאי האנגלי תומאס יאנג בשנת 1801. הניסוי הראה שהאור מתנהג כגל. השלכות הניסוי היו מכריעות; הן הניעו שני שינויים יסודיים בתפיסת המהות הפיזיקלית של האור:
- המעבר מהתיאור של ניוטון את קרינת האור כשטף חלקיקים המכונים פוטונים, למושג הגל האלקטרומגנטי;
- המעבר מתיאור החומר לפי התפיסה הקלאסית של חלקיקים, לתפיסה משולבת של גלים־חלקיקים.
רקע - תפיסת האור טרם הניסוי[עריכת קוד מקור | עריכה]
עד ביצוע הניסוי, רווחו בקרב הפיזיקאים שתי תפיסות שונות בנוגע למהותו של האור, כשאחת מהן נחשבה לטובה יותר. המודל החלקיקי, אותו קידם הפיזיקאי אייזק ניוטון, גרס שהאור הוא אוסף של חלקיקים. תפיסה שנייה בנוגע לאור הייתה התפיסה שהציג הפיזיקאי כריסטיאן הויגינס בשנת 1690, שייצגה את האור כתופעה גלית. לפי תפיסה זו האור הוא גל תלת־ממדי כדורי, המתפשט בתווך הנקרא אתר. הויגנס אף שיער שמהירות גלי האור היא סופית, כפי שהדגים אולה רמר כבר בשנת 1679. יאנג ביצע את ניסוי פיצול האור על מנת להכריע בין שתי התפיסות הללו, זו החלקיקית וזו הגלית.
הניסוי[עריכת קוד מקור | עריכה]
הניסוי המקורי בוצע באור ב-1801, על ידי הפיזיקאי תומאס יאנג, במטרה להכריע אם האור הוא גל או חלקיק.
בניסוי, יאנג הצליח לפצל את אלומת אור השמש לשתי אלומות נפרדות בעזרת "קלף" דק שהוצב בצורה אנכית לכיוון האור. כתוצאה מכך, האור הפגין התנהגות גלית, והציג תופעות של התאבכות ועקיפה.
מערך הניסוי[עריכת קוד מקור | עריכה]
ניסוי ראשון[עריכת קוד מקור | עריכה]
- מקור הפולט אור בקצב הנשלט על ידי מבצע הניסוי;
- מערך גלאים הרגיש לפגיעת חלקיקי אור וספירת החלקיקים אשר פגעו בכל נקודה במסך. במקרה של אור אפשר להשתמש במסך פשוט, ולראות ויזואלית את כמות החלקיקים אשר פגעו בכל נקודה בו - ככל שנקודה במסך בהירה יותר כך פגעו בה חלקיקים רבים יותר;
- מחיצה ובה שני סדקים דקים, אשר ניתנים לפתיחה וסגירה באופן בלתי תלוי. בניסוי המקורי שני סדקים היו פתוחים לכל אורך הניסוי.
תוצאות הניסוי[עריכת קוד מקור | עריכה]
איור המסכם את התוצאות[עריכת קוד מקור | עריכה]
תוצאות הניסוי מתוארות באיור הבא:
הקרנת פוטונים (אור)[עריכת קוד מקור | עריכה]
- כאשר פתחו סדק אחד קיבלו תבנית על המסך שמרכזה הבהיר ביותר נמצא מול הסדק שנפתח, והבהירות יורדת ככל שמתרחקים מנקודה זו עם מקטעים חשוכים במרחקים שווים (לפי עקרון העקיפה של פרנהופר);
- כאשר פתחו את שני הסדקים קיבלו תבנית התאבכות - פסים בהירים וכהים לסירוגין לאורך המסך. זו התנהגות שמתאימה לגלים.
הקרנת אלקטרונים[עריכת קוד מקור | עריכה]
בתחילת המאה ה-20, האלקטרונים נחשבו לחלקיקים מובהקים, ולכן ציפו שהם יראו התנהגות חלקיקית בניסוי, כלומר: כאשר שני הסדקים פתוחים רוב האלקטרונים יתרכזו מול כל אחד מהסדקים.
בפועל התוצאות היו שונות:
- כאשר פתחו סדק אחד האלקטרונים התנהגו כמו חלקיקים;
- כאשר פתחו את שני הסדקים ביחד - במקום לקבל פס רציף מול הסדקים התקבלה תבנית התאבכות (פסים עם הרבה ומעט אלקטרונים לסירוגין לאורך המסך) כאילו האלקטרונים היו גלים.
היה ניסיון להסביר זאת באמצעות הסתברות של זרם חלקיקים שמתנהג כמו גל, כלומר, אינטראקציה כלשהי בין האלקטרונים לבין עצמם, אך ניסוי שבו כל אלקטרון שוגר לחוד (לא שוגר אלקטרון אחר כל עוד האלקטרון הקודם לא פגע במסך) הראה תוצאות זהות - תבנית ההתאבכות נשארה. תופעה זו ניתנת להסבר על ידי כך שהאלקטרון (או בעצם פונקציית הגל שלו) עובר בו-זמנית דרך שני הסדקים, כפי שמנבאת המכניקה הקוונטית.
מסקנות מהניסוי[עריכת קוד מקור | עריכה]
המסקנה הבלתי נמנעת מהניסוי היא שלאלקטרון יש תכונות גליות. הניסוי גם מראה שאלקטרונים יכולים לבצע התאבכות ואף מוזר מכך - אלקטרון בודד יכול לבצע התאבכות עם עצמו. כלומר, לאלקטרון יש פונקציית גל (במובן של פונקציה הפותרת את משוואת הגלים ומתארת ישות בעלת תכונות של גל) המתפרשת על פני כל המרחב (ולכן יכולה לבצע התאבכות דרך שני סדקים).
עוד מסקנה מהניסוי היא שכאשר בודקים תכונות חלקיקיות של האלקטרון, הבדיקה מתגלית כחיובית; וכאשר בודקים תכונות גליות של האלקטרון, הבדיקה מתגלית כחיובית אף היא. כלומר, כמו האור, גם האלקטרון מקיים דואליות גל-חלקיק.
השאלה "באיזה מובן האלקטרון הוא גם גל", לא נפתרת על ידי ניסוי זה. אמנם במכניקת הקוונטים האלקטרון זוכה לפונקציית גל כאשר פונקציית הגל בערכה המוחלט בריבוע (אמפליטודה בריבוע) מתארת את ההסתברות למדוד את האלקטרון במקום (בנקודה מסוימת במרחב), אך יש חילוקי דעות לגבי משמעות פונקציית הגל, כאשר הפירוש ההסתברותי הוא המקובל ביותר, אם כי לא חף מבעיות.
וריאציות על הניסוי[עריכת קוד מקור | עריכה]
- התקנת גלאי על אחד הסדקים (כאשר שניהם פתוחים) בהקרנת אלקטרונים.
- התוצאה: הגלאי הראה באיזה סדק עובר כל אלקטרון, אך תבנית ההתאבכות נעלמה מהמסך ובמקומה התקבלה ההתפלגות הצפויה של חלקיקים.
- התקנת גלאי על אחד הסדקים בניסוי הקרנת פוטונים.
- לפי עקרון אי-הוודאות, מידת הרזולוציה של הגלאי קובעת את התוצאות. אם הגלאי בעל רזולוציה גבוהה, הפעלתו מפריעה לפוטונים והורסת את ההתאבכות. אם הגלאי בעל רזולוציה נמוכה מספיק לא להפריע לתבנית ההתאבכות, הדיוק שלו נמוך מדי מכדי לומר מאיזה סדק נכנס הפוטון.
במכניקת הקוונטים תופעה זו ידועה בשם אפקט הצופה.
ניתוח מתמטי[עריכת קוד מקור | עריכה]
מיקום השיאים (קווי האור) והשקעים (קווי החושך)[עריכת קוד מקור | עריכה]
השיא הראשון ממוקם מול מרכז הקו המחבר את שני הסדקים ( באיור). את מיקומם של שאר השיאים ניתן לאפיין בעזרת הזווית . מיקום קווי האור (התאבכות בונה) נתון על ידי:

ואילו מיקום קווי החושך (התאבכות הורסת) נתון על ידי:
כאשר
- הוא אורך הגל של האור המוקרן
- הוא המרחק בין הסדקים
- הוא מספר טבעי המייצג את הסדר של השיא (ככל שהסדר גבוה יותר, השיא פחות בהיר)
בקירוב של התאבכות פראונהופר בו הזוויות המדוברות קטנות (מסך רחוק מאוד) מקבלים:
- ( הוא המרחק בין הסדקים לקיר)
כאשר הוא ההיטל של קרן האור על המסך.
כך לדוגמה, המינימום הראשון נמצא ב-
בנוסף, ייתכנו מצבים בהם יש הפרש מופע בין שני הסדקים, שיכול להיגרם ממספר סיבות, כמו הנחת מקור האור במקום שאינו נמצא על האנך האמצעי. במקרים כאלו, תבנית ההתאבכות תזוז למטה או למעלה.
ההפרדה בין רצועות האור[עריכת קוד מקור | עריכה]
המרחק בין פסי האור נתון בקירוב על ידי
- כאשר:
הוא אורך הגל של האור המוקרן;
הוא המרחק בין הסדקים;
הוא המרחק בין הסדקים לקיר.
נוסחה זו היא מקורבת ונכונה רק בתנאים מסוימים (לרבות קירוב זוויות קטנות).
תבנית ההתאבכות והתמרת פוריה[עריכת קוד מקור | עריכה]
נגדיר פונקציה המחזירה את עוצמת האור שעוברת דרך נקודה במחסום עבור כל שהוא המרחק האופקי ממרכז המסך. תבנית ההתאבכות המתקבלת על המסך היא התמרת פורייה הרציפה של אותה הפונקציה כאשר במקום (התדירות המרחבית) מציבים . כאשר היא הזווית ממרכז המחסום לנקודה המסוימת במסך ו- הוא אורך הגל. דבר זה נכון עבור כל מחסום שהוא זהה אנכית.
קריסטלוגרפיה[עריכת קוד מקור | עריכה]
כפי שהוסבר בפיסקה הקודמת מתוך תבנית ההתאבכות ניתן ללמוד על העצם שדרכו עבר האור. במקרה של שני הסדקים מתוך תמונת ההתאבכות ניתן ללמוד על הרוחב של הסדקים והמרחק ביניהם, אך באופן כללי תמונת ההתאבכות נותנת התמרת פוריה של הסדקים דרכם עבר האור. מסיבה זאת נעשה שימוש רחב בהתאבכות על מנת לחקור חומרים, החל מגבישים ועד מולקולות ביולוגיות, ומדע זה נקרא קריסטלוגרפיה.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- ירון גרוס, הדואליות של החומר – ניסוי החריץ הכפול, במדור "מאגר המדע" באתר של מכון דוידסון לחינוך מדעי, 2 ביולי 2011
- קטע מתוך סדרת המדע הפופולרי ″Through the Wormhole″ : שחזור והסבר לניסוי שני הסדקים בקנה מידה מאקרוסקופי על ידי טיפות סיליקון על פלטת נוזל רוטטת, שחזור הניסוי בוצע על ידי הפיזיקאי הצרפתי איב קודיי.
- Dr. Quantum - Double Slit Experiment - סרטון המתאר את הניסוי באופן פופולרי
- ניסוי שני הסדקים, באתר אנציקלופדיה בריטניקה (באנגלית)

















