מכניקת הקוונטים
מכניקת הקוונטים (באנגלית: Quantum mechanics), או בשמות אחרים: פיזיקה קוונטית, תורת הקוונטים, מֵכָנִיקָה קְוַנְטִית או QM, היא תורה פיזיקלית המתארת את התנהגות הטבע בקני מידה קטנים ביותר או בטמפרטורות נמוכות[1] מאוד, עם השלכות על תחומי הפיזיקה בכל הסקאלות. התורה מספקת תיאור כמותי ויכולת ניבוי של שלל תופעות שלא ניתנות להסבר במסגרת המכניקה הקלאסית (זו שקדמה למכניקת הקוונטים) והאלקטרודינמיקה הקלאסית.
את מרבית התאוריות הקלאסיות ניתן לקבל כגבול של מכניקת הקוונטים, ממש כשם שהמכניקה הניוטונית מתקבלת כגבול של תורת היחסות הכללית. התאוריות המודרניות הללו, שהפכו את פני הפיזיקה בתחילת המאה ה-20, מכילות את שקדם להן כמקרה קצה ומרחיבות לתיאור נכון ומדויק יותר של הטבע. על אף ניסיונות רבים (כמו תורת המיתרים ותורת כבידה קוונטית), טרם נמצאה חד-משמעית תורה המאחדת את תורת הקוונטים עם תורת היחסות הכללית.
במכניקת הקוונטים, תכונות פיזיקליות מדידות מסוימות, כמו רמות האנרגיה באטום של מימן, מקבלות ערכים בדידים (דיסקרטיים, "מקוונטטים") ולא רציפים. תופעה זו נקראת "קווינטוט", או קוונטיזציה, והמרווחים הקטנים ביותר בין הערכים הבדידים נקראים קוונטה (קוונטום - מלטינית: כמות). גודל של קוונטום טיפוסי משתנה ממערכת למערכת.
תחת תנאים ניסיוניים מסוימים, עצמים קטנים מאוד, כמו אטומים או אלקטרונים, מגלים התנהגות גלית, כמו התאבכות. תחת תנאים אחרים, אותם עצמים מגלים תכונות של חלקיק (עצם שניתן לומר בוודאות באיזה תחום מרחבי הוא נמצא), למשל פיזור. תופעה זו נקראת דואליות גל-חלקיק. על פי מכניקת הקוונטים, דואליות זו קיימת בעצמים מכל סדר גודל. עבור עצמים מאקרוסקופיים אורכי הגל כה קצרים עד כי לא ניתן להבחין בתכונות הגליות כלל.
מכניקת הקוונטים היא תורה הסתברותית. כלומר, בניגוד למכניקה הקלאסית, במקרה הכללי מכניקת הקוונטים אינה יכולה לחזות איזו תוצאה תתקבל בניסוי, אלא רק את ההסתברות לקבל אותה. מבדיקות שנעשו על צבר של ניסויים זהים, התפלגות התוצאות שהתקבלה התאימה בדיוק רב לחיזוי שסיפקה מכניקת הקוונטים.
יישומים של התאוריה הקוונטית כוללים לייזרים, שבבים מוליכים למחצה, מוליכי על, מחשוב קוונטי, מכשור רפואי (כמו MRI), מכשירי תקשורת ועוד. חלק גדול מהטכנולוגיה שבה משתמשים כיום מבוסס על מכניקה קוונטית.
היסטוריה[עריכת קוד מקור | עריכה]
 ערך מורחב – היסטוריה של מכניקת הקוונטים
ערך מורחב – היסטוריה של מכניקת הקוונטים
ההשערה אודות קוונטיזציה של גדלים פיזיקליים הופיעה לראשונה במאמר של מקס פלאנק משנת 1900, העוסק בקרינת גוף שחור. פלנק ניסה במשך שנים להסביר את אופן הנצפה של התפלגות אורכי הגל של הקרינה, עד שלבסוף מצא נוסחה מדויקת לאחר שהניח שהאנרגיה הכוללת של המערכת עשויה ממנות בדידות (כלומר מקוונטות). פלנק, כפי שהעיד במכתבים מאוחרים יותר, חשב שהנחה זו מועילה לפתרון הבעיה ותו לא, ולא ייחס לה בתחילה חשיבות רבה.[2] בשנת 1905 פרסם אלברט איינשטיין מאמר אודות תכונותיו של האור. במאמר שיער שקרינה אלקטרומגנטית איננה גלים רציפים, כפי שהיה מקובל לחשוב בתקופה זו, אלא עשויה ממנות בדידות של אנרגיה, שמאוחר יותר קיבלו את השם פוטונים. הוא הראה כיצד ההשערה מסבירה תופעות שונות, בין השאר את האפקט הפוטואלקטרי. בניגוד לפלנק, איינשטיין הבין מיד שמדובר בהשערה מהפכנית.[2]

רעיון הקוונטיזציה הוסיף להתפשט בהדרגה ובאיטיות, ופורסמו תאוריות נוספות בתחומים שונים שעשו בו שימוש. לדוגמה, מודל האטום של בוהר משנת 1913 אימץ את המודל הפלנטרי לפיו האלקטרונים סובבים את גרעין האטום באופן הדומה לכוכבי לכת במערכת השמש, אך בתוספת אילוץ קוונטי: רמת האנרגיה שלהם ניתנת לאפיון על ידי מספר קוונטי טבעי, ולכן הם יכולים לנוע רק באחד מבין אוסף בדיד של מסלולים אפשריים. המודל הצליח להסביר תופעות שונות של אטום המימן, אך המאמצים המוקדמים להכלילו לאטומים נוספים נתקלו בקשיים.[3]
התאוריות השונות שהתפרסמו עד שנת 1925 מכונות באופן קולקטיבי בשם "תיאורית הקוונטים הישנה". הן התאפיינו בשילוב בין פיזיקה קלאסית עם תוספת של עקרונות קוונטים, שנראה שנוספו באופן אד הוק וחסר הצדקה, והיה קשה להכלילן מעבר לבעיה הנקודתית אותה הן פתרו. הדבר חידד את ההבנה שדרושה תאוריה חדשה שתחליף כליל את הפיזיקה הקלאסית, ותשנה את המושגים הפיזיקליים באופן רדיקלי. כמו כן הלך והתברר שהתאוריה החדשה עתידה לזנוח את הדימויים הוויזואליים השאולים מהפיזיקה הקלאסית, כגון חלקיק הנע במסלול בעל צורה גאומטרית נתונה, ולהסתמך במקום זאת על מושגים מתמטיים מופשטים כגון מספר קוונטי והסתברות מעבר.[4][3]
המונח "מכניקת הקוונטים" נטבע ב-1924 על ידי מקס בורן, ושנה לאחר מכן פרסם יחד עם ורנר הייזנברג ופסקואל יורדן תאוריה מלאה של מכניקת קוונטים המבוססת על חשבון מטריצות. במקביל פיתח פול דיראק תאוריה שקולה בשיטות מתמטיות אחרות. בשנת 1926 פרסם ארווין שרדינגר תאוריה נוספת, שהתגלתה גם היא כשקולה, המבוססת על גלים, ובבסיסה משוואת שרדינגר. שרדינגר הושפע בעבודתו זו מהשערת דה ברויי של לואי דה ברויי משנת 1924, לפיה כל חלקיק מתנהג כגל בתנאים מסוימים, והקשר בין התנע ואורך הגל זהה לזה שגילה איינשטיין במאמרו מ-1905 אודות חלקיקי האור.[5][2] זמן קצר לאחר פרסומה הציע בורן את הפרשנות לפיה גודל הגל במיקום נתון מייצג את ההסתברות למצוא את החלקיק באותו מיקום, וטען שהפיזיקה של האטום היא אינדטרמינסיטית.[4]
בשנים שלאחר מכן התגבשו עקרונות שקבעו בוהר ואחרים ונודעו באופן קולקטיבי כפרשנות קופנהגן. לפי פרשנות זו, אם חוקי מכניקת הקוונטים אינם מנבאים תוצאת מדידה של תכונה מסוימת באופן חד משמעי, הרי שהתכונה הזו אינה מוגדרת כלל. למשל, אם החוקים אינם מנבאים מיקום מדויק לחלקיק, אלא רק באופן הסתברותי, הרי שלחלקיק אכן אין מיקום מוגדר. איינשטיין התנגד לפרשנות זו, וראה באי הוודאות של מכניקת הקוונטים עדות להיותה תיאור לא שלם של הטבע, ולא תכונות של הטבע עצמו. בשנת 1926 כתב למקס בורן מכתב, ממנו צוטטה לאחר מכן בפרפרזה האימרה אלוהים לא משחק בקוביות. בעקבות איינשטיין, ניסה גם שרדינגר להראות שפרשנות קופנהגן עלולה להוביל לאבסורד, על ידי ניסוי מחשבתי שנודע כחתול של שרדינגר. בניסוי זה חתול מוחזק בכלוב ליד חומר רדיואקטיבי, ועל פי פרשנות קופנהגן לכאורה החתול ייכנס למצב שהוא תערובת של חי ומת בו זמנית.[5][6] הניסיונות לערער על מעמדה הפופולרי של פרשנות קופנהגן כשלו, אך ויכוחים סביב המשמעויות והפרשנויות של מכניקת הקוונטים נמשכים עד ימינו.
מאפיינים של מכניקת הקוונטים[עריכת קוד מקור | עריכה]
קוונטיזציה[עריכת קוד מקור | עריכה]
 ערך מורחב – קוונטיזציה (פיזיקה)
ערך מורחב – קוונטיזציה (פיזיקה)
על פי מכניקת הקוונטים גדלים פיזיקליים מסוימים אינם רציפים אלא כפולות שלמות של קבוע פיזיקלי כלשהו. במקרה זה נאמר עליהם שהם מקוונטטים, כלומר עשוים מקוונטות (מנות). זהו גם מקור שמה של מכניקת הקוונטים.[7]
לדוגמה, במודל הקוונטי של האטום מסלולו של כל אלקטרון סביב הגרעין מאופיין על ידי ארבעה מספרים טבעיים הקרויים מספרים קוונטיים. כך למשל המספר הקוונטי היסודי, המסומן באות n, מאפיין את רמת האנרגיה של האלקטרון וגם את מרחקו הממוצע מהגרעין. הערכים הללו יכולים לקבל מספרים טבעיים בלבד. אלקטרון הנמצא ברמה הקרובה ביותר לגרעין, n=1, יכול לקפוץ לרמה n=2, אך לא קיימת כל אפשרות להימצא ברמת ביניים ביניהן, או ברמה הקרובה יותר לגרעין מאשר n=1.[8]
הקווינטוט של גדלים נובע מכך שהמצבים החוקיים של מערכת, והאופן שבו היא משתנה עם הזמן, מוגדרים על ידי משוואת שרדינגר. כשפותרים אותה תחת אילוצים מסוימים מקבלים תוצאות המאופיינות על ידי מספרים שלמים.
דוגמה נוספת היא חלקיק הסגור בתוך קופסה, אך חופשי לנוע בה (דוגמה תאורטית נפוצה בספרות הקרויה בור פוטנציאל אינסופי). כשמכניסים למשוואת שרדינגר את האילוץ הנובע מגבולות הקופסה שתוחמות את החלקיק, מתקבל גם כאן שיש לחלקיק רמות אנרגיה בדידות המאופיינות על ידי מספר קוונטי. כמו כן מתקבל שלעולם חלקיק כזה לא יוכל להימצא במנוחה (כלומר אנרגיה אפס איננה מצב אפשרי של המערכת).[9]
דואליות גל-חלקיק[עריכת קוד מקור | עריכה]
 ערך מורחב – דואליות גל-חלקיק
ערך מורחב – דואליות גל-חלקיק
על פי מכניקת הקוונטים כל חלקיק יכול לגלות תכונות של גל, וכל גל יכול לגלות תכונות של חלקיק. כך למשל אלקטרון, שהוא חלקיק, יכול לגלות תכונות של התאבכות. מצד שני, קרינה אלקטרומגנטית, תופעה שנחשבה במשך שנים רבות לתופעה גלית בלבד, עשויה בנסיבות מסוימות לגלות תכונות של שטף חלקיקים הקרויים פוטונים.
דוגמה מפורסמת לכך היא ניסוי שני הסדקים. אם יורים אלומת אלקטרונים לעבר קיר בעל שני סדקים, האלומה מתנהגת כגל. היא עוברת דרך שני הסדקים, ובמסך שמאחור מופיעה תבנית התאבכות. אך אם שמים גלאי ליד אחד הסדקים כדי לנסות ולראות מאין עוברים האלקטרונים, האלומה הופכת לשטף של חלקיקים שכל אחד מהם עובר רק דרך אחד מהסדקים, ותבנית ההתאבכות נעלמת.[10]
למעשה, העצמים בטבע אינם חלקיקים ואינם גלים, אלא עצם מסוג שלישי הכולל את המאפיינים של שניהם. דרך נפוצה לתאר חלקיק במכניקת הקוונטים היא בעזרת ייצוג מתמטי הקרוי פונקציית גל. לפונקציית הגל תכונות רבות המוכרות מתחום הגלים, כגון אורך גל, אך היא מייצגת מידע אודות חלקיק בדיד, וניתן לגזור ממנה פרטים על אודות המיקום שלו, המהירות שלו ותכונות אחרות. המידע הזה אינו שלם, אלא הסתברותי בלבד, כפי שמתואר להלן.[7]
אינדטרמיניזם[עריכת קוד מקור | עריכה]
מכניקת הקוונטים אינה מאפשרת לחזות תוצאות של מדידה במדויק, אלא רק באופן הסתברותי. מכיוון שכך, לא ניתן לאשש או להפריך חיזוי של מכניקת הקוונטים בניסוי אחד, אלא רק בסדרה של ניסויים חוזרים, ולאחר ניתוח סטטיסטי של התוצאות.
לדוגמה, נחזור שוב לדוגמת החלקיק הלכוד בתוך קופסה. פונקציית הגל של חלקיק במצב זה תכיל את כל המידע הידוע אודותיו, ובפרט היכן בתוך הקופסה הוא נמצא, אך מידע זה הסתברותי בלבד. היא לא תגדיר נקודה ספציפית שבה החלקיק נמצא, אבל נוכל לגזור ממנה את ההסתברות למצוא את החלקיק בכל נקודה ונקודה במרחב. גזירת ההסתברות נעשית על ידי העלאת פונקציית הגל בריבוע, דבר הידוע כפירוש בורן לפונקציית הגל.[9][11]
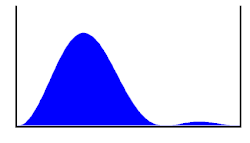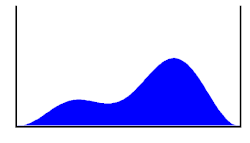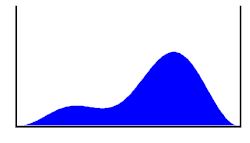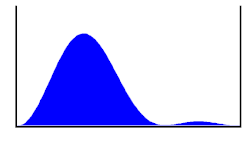
נניח שלפי פונקציית הגל ההסתברות למצוא את החלקיק בחציה השמאלי של הקופסה היא 90% (כדי לקבל נתון זה עלינו להעלות את הפונקציה בריבוע, ולבצע אינטגרציה שלה על המרחב הכלול בחצי זה של הקופסה, פעולה הדומה לסכימה). כמו כן נניח שברשותנו מכשיר גילוי המסוגל לבדוק האם החלקיק נמצא בחציה הימני של הקופסה, או בשמאלי, כלומר כשנפעיל את המכשיר נקבל כפלט "ימין" או "שמאל". על פי מכניקת הקוונטים, בניסוי בודד אין כל דרך לדעת מראש מה תהיה התוצאה, כי היא תבחר באופן אקראי, ולכן גם לא נוכל להסיק ממנה דבר. אך בסדרה ארוכה של ניסויים, למשל אם נחזור על הניסוי מיליון פעם, אז לפי חוק המספרים הגדולים, מספר הפעמים שנקבל כפלט "שמאל" צפוי להיות קרוב מאוד ל-90%, כפי שחישבנו מתוך פונקציית הגל. זוהי תחזית שניתן לאשש או להפריך, ולכן זהו חיזוי בעל משמעות מדעית.
בזמן שאנחנו מפעילים את מכשיר המדידה פונקציית הגל עוברת תהליך הקרוי קריסת פונקציית הגל, שבו היא משתנה בבת אחת. אם מכשיר המדידה החזיר לנו תשובה "שמאל", כלומר אכן החלקיק התגלה בחצי השמאלי, אז פונקציית הגל תשתנה כדי לשקף את המידע החדש הזה, וכעת היא תגדיר שהחלקיק נמצא בוודאות בחצייה השמאלי של הקופסה. ההסתברות למוצאו כעת בחצי הימני תצנח לאפס. וגם להפך: אם מכשיר המדידה החזיר "ימין", אז פונקציית הגל תקרוס כך שכעת ההסתברות למצוא את החלקיק בחצי השמאלי תצנח לאפס.
לכן כדי לבצע סדרה של ניסויים על מנת לאשש חיזוי של מכניקת הקוונטים, כפי שתואר לעיל, צריך להתחיל כל ניסוי בתהליך של הכנה שבו אנחנו מביאים את פונקציית הגל לערך ההתחלתי הרצוי שלה.[11]
מצב בו לחלקיק אין לתכונה מסוימת ערך אחד מוגדר, אלא התפלגות הסתברותית מעל אוסף ערכים אפשריים, קרוי סופרפוזיציה קוונטית. סופרפוזיציה יכולה להיות עבור תכונת המיקום במרחב, או לכל תכונה פיזיקלית אחרת. במחשב קוונטי למשל, יחידת המידע הבסיסית במחשב כזה היא קיוביט, ביט קוונטי היכול לקבל ערך של 0, 1, או להיות בסופרפוזיציה של קומבינציה כלשהי של שניהם.
עקרון האי-ודאות[עריכת קוד מקור | עריכה]
 ערך מורחב – עקרון האי-ודאות
ערך מורחב – עקרון האי-ודאות
עקרון האי-ודאות מציב גבול על היכולת לדעת במדויק את כל התכונות של חלקיק.
על פי עקרון האי-ודאות זוגות מסוימים של תכונות הם כאלה שלא ניתן לדעת במדויק את שתיהן בו זמנית. זוג כזה לדוגמה הוא המיקום במרחב והתנע (מכפלת המסה במהירות). לכן ככל שהמידע שיש לנו על אודות מיקום החלקיק מדויק יותר, כך בהכרח המידע שיש לנו על אודות התנע שלו יהיה בלתי מדויק, או בעל אי ודאות גבוהה. וגם להפך: ידע על התנע בהכרח גורר חוסר ידע על המיקום, ולא ניתן לעולם לדעת במדויק את שניהם.
זוג תכונות נוסף המקיים את עקרון האי-ודאות הוא אנרגיה וזמן.[12]
אפקט הצופה[עריכת קוד מקור | עריכה]
 ערך מורחב – אפקט הצופה
ערך מורחב – אפקט הצופה
כשמכשיר מדידה פועל, הוא נמצא באינטראקציה כלשהי עם העצם אותו הוא מודד. אינטראקציה זו עשויה להשפיע על העצם הנמדד, לשנות את מצבו, ובמקרים קיצוניים להרוס אותו כליל. לדוגמה, מכשיר מדידה לגילוי פוטונים בולע את הפוטון אגב הגילוי שלו, ומעלים אותו.[11] דוגמה נוספת: כדי לגלות אלקטרון, יורים עליו פוטונים, וכשפוטון פוגע באלקטרון מסלול האלקטרון משתנה.[13] השפעה של המדידה על המערכת הנמדדת קרויה אפקט הצופה.
על פי הפיזיקה הקלאסית אפקט הצופה הוא תוצאת לוואי של המדידה שעקרונית ניתן למזערה ככל שנרצה בעזרת מכשירי מדידה משוכללים יותר. לעיתים קרובות כשדנים בבעיות תאורטיות בפיזיקה קלאסית מניחים את קיומם של מכשירי מדידה אידיאליים שאינם משפיעים כלל על המערכת הנמדדת.
על פי מכניקת הקוונטים, לעומת זאת, אפקט הצופה הוא בעל משמעות רבה, ואין כל דרך למזער אותו ברמה שניתן יהיה להתעלם ממנו. לפני שמתבצעת מדידה, החלקיק יהיה במצב של סופרפוזיציה, כלומר פונקציית הגל שלו תגדיר התפלגות כלשהי של ערכים אפשריים. בזמן המדידה פונקציית הגל קורסת, ואחד הערכים נבחר באקראי. פונקציית הגל כעת מייצגת את המידע החדש שהתקבל על ידי מכשיר המדידה, ולכן שונה מכפי שהייתה קודם לכן. הדבר ישפיע על המשך התפתחות החלקיק מכאן והלאה, וכן ישפיע על מדידות נוספות שיתבצעו עליו.[13][11]
דוגמה מפורסמת לאפקט הצופה היא ניסוי שני הסדקים, כפי שתואר לעיל. אם לא צופים באלומת האלקטרונים, פונקציית הגל שלה לא מופרעת, עוברת דרך שני סדקים, ותבנית התאבכות מופיעה. אך אם שמים גלאי ליד אחד הסדקים, פונקציית הגל קורסת ותבנית ההתאבכות נעלמת.[10]
חוסר לוקליות[עריכת קוד מקור | עריכה]
על פי הפרדוקס של איינשטיין-פודולסקי-רוזן, ניתן לתאר במכניקת הקוונטים מצב שבו שני חלקיקים עוברים הכנה כלשהי יחדיו, ולאחר מכן אפשר להפריד ביניהם למרחק שרירותי, ובכל זאת הם יישארו קשורים זה לזה באופן כלשהו. הקשר ביניהם מתבטא בכך שתוצאת מדידה המתבצעת על אחד מהם, תשליך על תוצאת המדידה שתתבצע לאחר מכן על השני, דבר הסותר לכאורה את עקרון המקומיות.
באחד מהניסוחים השונים של הפרדוקס, החלקיקים עוברים הכנה כזו שהספין שלהם ביחס לציר נתון נמצא במצב לא ידוע, אך בהכרח מנוגד זה לזה. כלומר על פי פונקציית הגל שלהם הספין שלהם הוא או כלפי מעלה או כלפי מטה, בהסתברויות שוות, וידוע רק שאם לאחד ספין כלפי מעלה אז לשני ספין כלפי מטה, ולהפך. לאחר מכן מפרידים ביניהם למרחק גדול מאוד, ומודדים את הספין של האחד ביחס לציר הנתון. אם התקבלה תוצאה 'למעלה', אז מתחייב מכך שמדידת החלקיק השני תניב תוצאה 'למטה', ולהפך.
על פי פרשנות קופנהגן, הספין של שני החלקיקים לא היה מוגדר כלל עד ביצוע המדידה הראשונה. אם המדידה של החלקיק הראשון הניבה תוצאה 'למעלה', הרי שבאותו רגע הספין שלו הפך למוגדר, ומופנה כלפי מעלה. המידע הזה לכאורה שודר בזמן אפס למרחק רב לעבר החלקיק השני, כך שהוא 'ידע' להתאים את עצמו ולהגדיר לעצמו את הספין בכיוון ההפוך.
איינשטיין ועמיתיו התכוונו בפרדוקס זה להפריך את פרשנות קופנהגן, מכיוון ששידור מידע מהר יותר ממהירות האור סותר את תורת היחסות הפרטית. הם הציעו פרשנות אלטרנטיבית: הספין של החלקיקים בעצם כבר נקבע מראש, והעובדה שפונקציית הגל שלהם לא כללה מידע זה היא הוכחה שמכניקת הקוונטים עצמה אינה שלמה. הפרשנות הזו היא דוגמה לתאוריות משתנים חבויים, לפיהן העצמים מכילים מידע נוסף, שאינו מתואר על ידי פונקציית הגל שלהם.
לבסוף הופרכה הפרשנות של איינשטיין על ידי תוצאה הידועה כמשפט בל. המשפט הפריך את הפרשנות של איינשטיין כמו גם חלק מתאוריות המשתנים החבויים האחרות. התופעה של קשר בין חלקיקים מרוחקים כונתה לאחר מכן שזירה קוונטית, והוכח שעל אף שהיא קיימת, אין אפשרות להשתמש בה על מנת לשדר מידע מהר יותר ממהירות האור, ולכן אין בה סתירה מהותית לתורת היחסות הפרטית, כפי שחשבו איינשטיין ועמיתיו בתחילה.[7]
קנה מידה ועקרון ההתאמה[עריכת קוד מקור | עריכה]
מכניקת הקוונטים פותחה על מנת להתמודד עם תופעות הקשורות בעצמים בקנה מידה קטן, אטומים וחלקיקים תת-אטומיים. עם זאת, היא מקיימת את עקרון ההתאמה של בוהר, לפיו אם מציבים בנוסחאות של מכניקת הקוונטים גדלים המתארים עצמים בקנה מידה אנושי רגיל, כגון כדור טניס או מכונית, אזי מקבלים תוצאות זהות בקירוב לאלה של הפיזיקה הקלאסית.
לדוגמה, לפי עקרון האי-ודאות מכפלת האי-וודאויות של מיקום ותנע אינה יכולה להיות נמוכה מ- כאשר h הוא קבוע פלאנק השווה בערך ל- ביחידות של ג'ול לשנייה. זהו גודל משמעותי רק עבור קנה מידה אטומי או תת-אטומי, ולכן עקרון האי-ודאות לא מורגש בקנה המידה של הפיזיקה הקלאסית.[12]
פורמליזם מתמטי[עריכת קוד מקור | עריכה]
 ערך מורחב – הפוסטולטים של תורת הקוונטים
ערך מורחב – הפוסטולטים של תורת הקוונטים
מקובל להגדיר את הבסיס המתמטי של מכניקת הקוונטים על ידי רשימת פוסטולטים (אקסיומות), אף כי אין דרך אחת אחידה לעשות כן.[14][15][16] להלן נציג כמה פוסטולטים בליווי הסברים בסיסיים, תוך שימוש בסימון דיראק, סימון מתמטי מקובל במכניקת הקוונטים.
פוסטולט ראשון: מרחב המצבים[עריכת קוד מקור | עריכה]
מערכת פיזיקלית מאופיינת על ידי מרחב הילברט שמהווה את מרחב המצבים שלה. כל אבר במרחב זה מגדיר באופן מלא מצב אפשרי אחד של המערכת.
נסביר פוסטולט זה בתחילה עם דוגמה מהפיזיקה הקלאסית. נניח שיש חלקיק בודד בקופסה. ניתן לאפיין את מצבו של החלקיק בפיזיקה קלאסית בעזרת וקטור מיקום p, ווקטור מהירות v. הזוג (p,v) לכן הוא תיאור מלא של מצב אפשרי אחד של המערכת (נניח לשם פשטות שאין תכונות נוספות מלבד מיקום ומהירות שמשפיעות על המערכת). למשל זוג הווקטורים ((0,0,0),(0,0,0)) מתאר מצב בו החלקיק נמצא בראשית הצירים ומהירותו אפס. מרחב המצבים של המערכת הוא קבוצת כל הזוגות (p,v) האפשריים.
במכניקת הקוונטים מצב של המערכת, המכונה גם מצב קוונטי, מיוצג על ידי וקטור בעל ממד גבוה, בדרך כלל אינסופי, או פונקציית גל (שגם בה אפשר לראות וקטור בעל ממד אינסופי). הפוסטולט לא מגדיר באיזה אופן המצב הקוונטי מתאר תכונות מדידות כגון מיקום ומהירות, והדבר יוגדר בפוסטלט השלישי. בסימון דיראק אבר במרחב המצבים מסומן ומכונה "קֵט" (ket).
הפוסטולט מציין שמרחב המצבים אינו קבוצה סתם אלא מרחב הילברט, וזוהי אמירה משמעותית. למרחב הילברט תכונות מתמטיות מסוימות, ולכן הפוסטולט אומר למעשה שתכונות אלה יתקיימו בכל מערכת פיזיקלית. תכונה אחת כזו למשל היא סגירות לפעולות חיבור וכפל בסקלר. לכן אם ו- הם מצבים במרחב, אז בהכרח מצב אפשרי של המערכת הוא כל צירוף ליניארי שלהם, , כאשר a ו-b הם מספרים מרוכבים כלשהם. כפי שנראה בהמשך, הפוסטולט השלישי ייתן לכך משמעות של סופרפוזיציה. תכונה נוספת של מרחב הילברט היא קיומה של פעולה הקרויה מכפלה פנימית בין שני איברים, ומסומנת: . תוצאת המכפלה הזו היא מספר מרוכב (משמע סקלר). הפוסטולטים הבאים יעשו שימוש בתכונות אלה.
פוסטולט שני: התפתחות בזמן[עריכת קוד מקור | עריכה]
ההתפתחות בזמן של מצב קוונטי מוגדרת על ידי משוואת שרדינגר, , כאשר H הוא ההמילטוניאן המייצג את האנרגיה של המערכת.
במכניקה הקלאסית, אם ידוע מצב המערכת בזמן נתון, ניתן לחשב את מצבה בכל זמן בעתיד על ידי חוקי התנועה של ניוטון.
במכניקת הקוונטים האופן שבו משתנה המערכת מוגדר על ידי משוואת שרדינגר. אם מצב המערכת בזמן 0 הוא מצב ידוע , ניתן בעזרת המשוואה לחשב את מצב המערכת בכל זמן t בעתיד. משוואת שרדינגר היא דטרמיניסטית, ולכן חישוב זה הוא ודאי ומדויק. זאת בתנאי שלא מתרחשת בפרק הזמן זה מדידה, שעשויה לשנות את המצב באופן לא דטרמיניסטי, כפי שמוגדר בפוסטולט הבא.
פוסטולט שלישי: מדידה[עריכת קוד מקור | עריכה]
לכל גודל מדיד קיים אופרטור הרמיטי , ואוסף תוצאות המדידה האפשריות הן אוסף הערכים העצמיים של האופרטור, . אם התקבלה במדידה התוצאה אז לאחר המדידה המערכת תעבור למצב העצמי המתאים . אם מצב המערכת הנוכחי הוא מצב כלשהו , אז ההסתברות לקבל תוצאה היא , כלומר ריבוע המכפלה הפנימית בין המצב הנוכחי למצב העצמי המתאים ל-.
פוסטולט זה מגדיר מהי מדידה בעזרת כלים מתמטיים מופשטים, וכמה מקביעותיו הן המוזרות והשנויות במחלוקת ביותר במכניקת הקוונטים.[14]
אופרטור הוא אובייקט מתמטי המתאר פעולה, במקרה שלנו פעולה על המצב הקוונטי של המערכת. הפעלה של אופרטור על המצב הקוונטי גורמת לשינוי למצב קוונטי אחר. לדוגמה האופרטור משנה את המצב על ידי הכפלתו ב-x. למשל, אם המצב של המערכת מתואר על ידי פונקציית הגל אז לאחר הפעלת האופרטור פונקציית הגל תשתנה ל-. האופרטור משנה את המצב על ידי גזירת פונקציית הגל והכפלתה בקבועים . אם נפעיל אותו על אותה פונקציית גל מהדוגמה הקודמת, נקבל: .
לאופרטורים ייתכנו מצבים מיוחדים הקרויים מצבים עצמיים. כשאופרטור יופעל על אחד המצבים העצמיים שלו, השינוי היחיד שיחול בהם הוא הכפלה בקבוע. נסתכל לדוגמה על פונקציית הגל: . אם נפעיל עליה את האופרטור נקבל: . מכאן ש- היא פונקציית גל המתארת מצב עצמי של . כשמפעילים עליה את האופרטור היא מוכפלת ב-p. הקבוע p שבו היא מוכפלת קרוי ערך עצמי.
לפי הפוסטולט, כל גודל מדיד מיוצג על ידי אופרטור הרמיטי כלשהו. למשל, תנע מיוצג על ידי האופרטור שתואר לעיל. מכאן שלפי הפוסטולט, כשנפעיל מכשיר למדידת תנע, תוצאת המדידה תהיה אחד הערכים העצמיים של האופרטור (למשל, p), ולאחר המדידה מצב המערכת יהיה המצב העצמי המתאים (כלומר אם קיבלנו p, מצב המערכת כעת מתואר על ידי פונקציית הגל שהגדרנו לעיל).
תכונת ההרמיטיות של אופרטור מבטיחה שהערכים העצמיים שלו יהיו תמיד מספרים ממשיים. כך שאף על פי שמכניקת הקוונטים עושה שימוש נרחב במספרים מדומים, היא תמיד תנבא לתוצאות המדידה מספרים ממשיים.
נסתכל כעת על אופרטור כלשהו, , ועל שני מצבים עצמיים שלו ו-. על פי הפוסטולט הראשון, ניתן להרכיב מצב שהוא סופרפוזיציה של שניהם: . מהפוסטולט השלישי נובע כי אם נפעיל את המדידה אותה מייצג כאשר המערכת נמצאת במצב , אזי הסופרפוזיציה הזו תקרוס לאחד משני המצבים העצמיים, בהסתברות לראשון, ו- לשני, ותוצאת המדידה תהיה הערך העצמי המתאים.
תכונה מתמטית נוספת של אופרטור הרמיטי מבטיחה שאוסף המצבים העצמיים שלו מהווים בסיס למרחב כולו. פירוש הדבר, שעל ידי חיבור המצבים העצמיים עם מקדמים שונים (צירוף ליניארי) ניתן להגיע לכל מצב במרחב המצבים. מכאן שבכל רגע נתון ניתן לראות את מצב המערכת כסופרפוזיציה של המצבים העצמיים של כל אחד מהאופרטורים המייצגים גדלים מדידים.[14]
יצוין כי ניתן להגדיר אופרטורים קוונטים שאינם הרמיטיים, ולהם וקטורים עצמיים ימני ושמאלי וערכים עצמיים מרוכבים. אופרטור ההמילטוניאן, למשל, יהיה בעל ערך עצמי שחלקו המדומה, המסומן כ-Γ/2, מתאר את דעיכתה הגלובלית של פונקציית הגל במרחב הילברט בו היא מתקיימת. פורמליזם המכניקה הקוונטית הלא-הרמיטית נוח לתיאור מצבי רזוננס, להם חלק קשור וחלק חופשי, וכן לפתרון משוואת שרדינגר במערכות פתוחות או במערכות עם דיסיפציה (למשל, חיכוך או הדעכה בסיב אופטי). משוואת שרדינגר התלויה בזמן מקבלת בפורמליזם זה צורה של משוואת פלוקה (Floquet) בה הזמן הוא קואורדינטה, ולא פרמטר. על ידי שימוש בפורמליזם הלא-הרמיטי ניתן לגזור בפשטות יחסית מספר מסקנות חשובות לגבי אפקט שטארק ו"מצבים מולבשים", המשותפים לאלקטרון ולפוטון.
ראו גם[עריכת קוד מקור | עריכה]
|
עיינו גם בפורטל פורטל הפיזיקה מהווה שער לחובבי הפיזיקה ולמתעניינים בתחום. בין היתר, בפורטל תוכלו למצוא מידע על פיזיקאים חשובים, על ענפי הפיזיקה ועל תאוריות פיזיקליות. |
מושגים בסיסיים[עריכת קוד מקור | עריכה]
- סימון דיראק
- משוואת שרדינגר
- עקרון אי הוודאות
- פונקציית גל
- מצב קוונטי
- משפט ארנפסט
- סופרפוזיציה
- קריסת פונקציית הגל
- שניות גל-חלקיק
ניסויים ותופעות[עריכת קוד מקור | עריכה]
- ניסוי שני הסדקים
- קרינת גוף שחור (קרינה תרמית)
- האפקט הפוטואלקטרי
- ספקטרום פליטה
- תיקוני המבנה הדק (fine structure)
- תיקוני המבנה העל-דק (hyper-fine structure)
כלים מתמטיים[עריכת קוד מקור | עריכה]
- המילטוניאן
- מרחב הילברט
- מכפלה פנימית
- אנליזה מרוכבת
- אנליזת פורייה (התמרת פורייה וטור פורייה)
- אופרטורים ומטריצות
- אופרטור הרמיטי ויוניטריות
- משוואות דיפרנציאליות
- תורת שטורם-ליוביל
- רנורמליזציה
- אלגבראות סי כוכב
- תורת ההפרעות
בעיות יסודיות[עריכת קוד מקור | עריכה]
- חלקיק חופשי ("גל מישורי")
- בור פוטנציאל אינסופי
- אוסצילטור הרמוני קוונטי
- ספין - אינטראקציה של ספין בשדה מגנטי
נושאים מתקדמים[עריכת קוד מקור | עריכה]
- בעיית המדידה
- סיבית קוונטית (qubit)
- שזירה (Entanglement)
- מטריצת צפיפות (Density Matrix)
- הפרדוקס של איינשטיין-פודולסקי-רוזן
- אינפורמציה קוונטית
- משוואת קליין-גורדון
- משוואת דיראק
- אינטגרל מסלולי של פיינמן
- קוונטיזציה ראשונה
- קוונטיזציה שנייה
- תורת השדות הקוונטית
- אנרגיית נקודת האפס
- אופטיקה קוונטית
שימושים ויישומים[עריכת קוד מקור | עריכה]
- רמות אנרגיה של אטומים ובייחוד, אטום המימן
- כימיה קוונטית
- תרמודינמיקה קוונטית
- פיזיקה גרעינית
- פיזיקה של חלקיקים והמודל הסטנדרטי
- פיזיקה של חומר מעובה
- אלקטרוניקה ואלקטרומגנטיות בחומר
- מחשב קוונטי
- הצפנה קוונטית
- טלפורטציה קוונטית
- מחסום פוטנציאל סופי
אנשים[עריכת קוד מקור | עריכה]
- אלברט איינשטיין
- מקס פלאנק
- לואי דה-ברויי
- נילס בוהר
- ארווין שרדינגר
- ורנר הייזנברג
- פול דיראק
- ג'ון פון ניומן
- מקס בורן
- ריצ'רד פיינמן
- יקיר אהרונוב
- אשר פרס
- בוריס צירלסון
פרשנויות של מכניקת הקוונטים[עריכת קוד מקור | עריכה]
- פרשנות קופנהגן
- פירוש העולמות המרובים
- תאוריות משתנים חבויים
- תאוריית דה ברויי-בוהם
- תאוריית גיררדי-רימיני-ובר
שונות[עריכת קוד מקור | עריכה]
לקריאה נוספת[עריכת קוד מקור | עריכה]
- טוביאס הירטר, עידן האי־ודאות - איך גילו גדולי הפיזיקאים את עולם הקוונטים 1895–1945, ספרי עליית הגג וידיעות ספרים, 2023.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- צבי ינאי, הוודאות האבודה של הטבע והאחדות הקוואנטית, מחשבות 55, אפריל 1988, עמ' 4–25
- יואב בן דב, מנות וגלים (על התפתחות תורת הקוונטים) וגם החלקיק והצופה (תורת הקוונטים - בעיות ופירושים), פרקים מתוך ספרו "פיזיקה - תורות ומושגים", הוצאת מערכת הביטחון
- יששכר אונא, תורת הקוונטים עדיין במבחן, מדע, מאי 1983.
- דוד גורביץ' ודן ערב, הערך "תיאוריית הקוונטים", באתר אנציקלופדיה של הרעיונות
- ירדן ניר-בוכבינדר, מתי מטיל אלוהים את הקוביות, באתר האייל הקורא.
- אבני דרך, עשר התגליות הגדולות בפיזיקה ובאסטרונומיה, באתר ifeel
- רועי בר, מבוא לקשר כימי רשימות ההרצאות - ׁ(בעברית).
- אבשלום אליצור, תורת הקוונטים: מה היא אומרת - ומה לא
 אפרים שחמון, מסע אל העולם המופלא לתורת הקוונטים, "טבע הדברים" (כפי שנשמר בארכיון האינטרנט)
אפרים שחמון, מסע אל העולם המופלא לתורת הקוונטים, "טבע הדברים" (כפי שנשמר בארכיון האינטרנט)- יוסי אברון, כאן, שם ובכל מקום, אודיסאה 8, יולי 2010
- על שזירה קוונטית במדור "המאור הקטן" באתר רשת ב'
- קִוְנוּט, קִוְנֵט, מְקֻוְנָט – quantize, quantization, quantized: גזירת שורש מן קְוַנְט, זיכרונות האקדמיה ללשון העברית נ-נא-נב-נג, ישיבה רסח, עמ' 45–47, באתר האקדמיה ללשון העברית
- מכניקת הקוונטים, באתר אנציקלופדיה בריטניקה (באנגלית)
 תורת הקוונטים, דף שער בספרייה הלאומית
תורת הקוונטים, דף שער בספרייה הלאומית גדעון לב, תיאוריה שמאחדת בין תורת היחסות למכניקת הקוונטים. הניסוי של דניאל ג'פריס, באתר הארץ, 5 באפריל 2023
גדעון לב, תיאוריה שמאחדת בין תורת היחסות למכניקת הקוונטים. הניסוי של דניאל ג'פריס, באתר הארץ, 5 באפריל 2023- תגלית מדעית: חוקרים ראו תופעות ממכניקת הקוונטים בתנועת מטוטלות, באתר ידיעות אחרונות, 3 במרץ 2024
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ L.D. Landau and E. M. Lifshitz, Statistical Physics, New York: pergamon press
- ^ 1 2 3 Helge Kragh, Quantum Generations: A History of Physics in the 20th Century, Princeton: Princeton University, Press, 1999, Chapter 5
- ^ 1 2 Seth, S. (2013-10-01). Quantum Physics. In (Ed.), The Oxford Handbook of the History of Physics. : Oxford University Press,. Retrieved 4 Aug. 2018, from http://www.oxfordhandbooks.com/view/10.1093/oxfordhb/9780199696253.001.0001/oxfordhb-9780199696253-e-28
- ^ 1 2 Helge Kragh, Quantum Generations: A History of Physics in the 20th Century, Princeton: Princeton University, Press, 1999, Chapter 11
- ^ 1 2 Darrigol, O. (2002). Quantum Theory and Atomic Structure, 1900–1927. In M. Nye (Ed.), The Cambridge History of Science (The Cambridge History of Science, pp. 329-349). Cambridge: Cambridge University Press. doi:10.1017/CHOL9780521571999.019
- ^ Helge Kragh, Quantum Generations: A History of Physics in the 20th Century, Princeton: Princeton University, Press, 1999, Chapter 14
- ^ 1 2 3 ששה דברים שכל אחד צריך לדעת על פיזיקת קוונטים, צ'אד אורזל, פורבס (אנגלית)
- ^ מבנה האטום: המודל הקוונטי באתר dummies
- ^ 1 2 חלקיק בקופסה חד-ממדית אתר LibreTexts
- ^ 1 2 תיאורית הקוונטים מודגמת: תצפית משנה מציאות, Science Daily (אנגלית)
- ^ 1 2 3 4 Visual Quantum Mechanics, ברנד ת'אלר
- ^ 1 2 https://www.britannica.com/science/uncertainty-principle עקרון האי-ודאות, אנציקלופדיה בריטניקה
- ^ 1 2 איך צפייה בניסוי בלי להתערב בו משפיעה על התוצאה, חיים ברק, אתר מכון דוידסון
- ^ 1 2 3 חומרי השלמה על סימון דיראק ומצבים קוונטים, ר. ל. יפה, רשימות לקורס של MIT (אנגלית)
- ^ הפוסטולטים של מכניקת הקוונטים, טוד א. ברון, הרצאה בקורס עיבוד אינפורמציה קוונטית, אוניברסיטת דרום קליפורניה (אנגלית)
- ^ הפוסטולטים של מכניקת הקוונטים, דייוויד שריל, מבוא למבנה אלקטרוני, המכון הטכנולוגי של ג'ורג'יה (אנגלית)
| תחומים בפיזיקה | ||
|---|---|---|
| פיזיקה קלאסית | אופטיקה • אלקטרומגנטיות • אסטרונומיה • אקוסטיקה • מכניקה (מכניקה קלאסית • מכניקת הזורמים • מכניקת הרצף) • תרמודינמיקה | |
| פיזיקה מודרנית | אלקטרואופטיקה • אסטרופיזיקה • פיזיקת חלקיקים • פיזיקה גרעינית • פיזיקת מצב מעובה • פיזיקה סטטיסטית • תורת היחסות (הכללית • הפרטית) • מכניקת הקוונטים • תורת השדות הקוונטית • תורת המיתרים • פיזיקה כימית | |
| נושאים בינתחומיים | ביופיזיקה • פיזיקה רפואית • גאופיזיקה • פיזיקה מולקולרית | |
| היסטוריה של הפיזיקה | היסטוריה של הפיזיקה עד המאה ה-20 • התפתחות הפיזיקה במאה ה-20 | |