גל
יש לערוך ערך זה. הסיבה היא: הסברים לא ממצים.
| ||
| יש לערוך ערך זה. הסיבה היא: הסברים לא ממצים. | |

בפיזיקה, גל הוא התפשטות (או התקדמות) של הפרעה (סטיה משיווי משקל) בתווך כשלהו או בשדה. לדוגמה, גל במים הוא הפרעה בגובה המים, גל קול הוא הפרעה בצפיפות האוויר, וגל אלקטרומגנטי הוא הפרעה בשדה החשמלי והמגנטי. מאופי השדה, ניתן לראות שיש גלים שיכולים להתפשט רק בחומר, כמו גלי קול או גלים במים, משום שגלים אלו הם הפרעה בשדות הקשורים לתווך עצמו, כמו צפיפותו או גובהו. לעומת זאת, קיימים גלים שיכולים להתפשט גם בריק, למשל גלים אלקטרומגנטיים. בדרך כלל, המונח "גל" מתאר הפרעה מחזורית בזמן. הפרעה שאיננה מחזורית בזמן נקראת פולס.
לגלים תכונות שונות מאוד משל חלקיקים, והם מראים תופעות מיוחדות כמו התאבכות, עקיפה ושבירה. במשך שנים רבות עסק המדע בשאלה האם אור הוא גל או חלקיק, אך כיום הבעיה נפתרה בעזרתה של מכניקת הקוונטים. על פי תורה זו, לכל חלקיק יש גם אופי גלי, תופעה הנקראת דואליות גל-חלקיק, ולכן תופעות גליות לוקחות חלק מכריע בתיאור העולם הקוונטי.
מאפייני הגל[עריכת קוד מקור | עריכה]
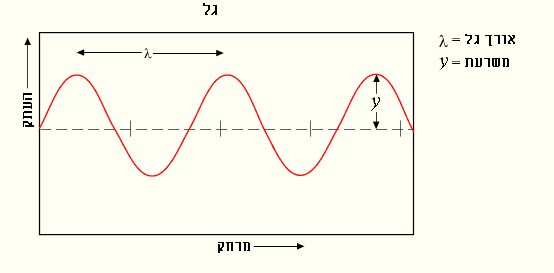
קיימים מספר מאפיינים או פרמטרים פיזיקליים המגדירים את הגל ואת התנהגותו.
- משרעת (או אמפליטודה בלעז) - גודל ההפרעה המקסימלי, ומסומנת באיור ב-, ולפעמים מסומנת ב-.
- אורך גל - המרחק בין שתי פסגות סמוכות של הגל. מסומן לרוב באות
- תדירות - מספר המחזורים ליחידת זמן, מסומנת לרוב באות f או באות .
- תדירות זוויתית - מאחר שבדרך כלל מתארים גלים על ידי פונקציות טריגונומטריות, נהוג לנרמל את התדירות, כך שהארגומנט יהיה כפולה של . לכן
- מספר הגל (וקטור הגל) - מספר הגל, המסומן לרוב ב , הוא המקביל המרחבי לתדירות הזוויתית. כשם שהתדירות הזוויתית מתקשרת לזמן המחזור על ידי , מספר הגל מתקשר לאורך הגל על ידי . בגלים במרחב רב ממדי, מוגדר וקטור גל, המציין את כיוון התקדמות ההפרעה, והנורמה שלו נתונה על ידי .
- כוון ההפרעה ביחס לכוון התנועה: גל אורכי הוא גל המורכב מהפרעה מתקדמת שכיוונה ככיוון התפשטות הגל, לדוגמה גל קול. לעומתו, גל רוחבי הוא גל שבו ההפרעה המתקדמת מאונכת לכיוון התקדמות הגל, לדוגמה גלים אלקטרומגנטיים. (הערה: יש הסבורים כי גלי מים הם גלים רוחביים אך צריך לשים לב כי גלי מים אינם רוחביים ואינם אורכיים)
- מהירות פאזה - מהירות ההתפשטות של חזית הגל. מסומנת ב-v ומוגדרת כ .
- מהירות חבורה - מהירות התקדמות האנרגיה (ריבוע אמפליטודת המעטפת) בחבורת גלים, מוגדרת על ידי יחס נפיצה כ .
כאשר , כמו בגלי סינוס למשל, הקשר בין שלושת הגדלים האחרונים ניתן באמצעות משוואת הגלים - .
מאפיין נוסף לקבוצת גלים הוא הפרש המופע (פאזה) או זווית המופע. גודל זה, המסומן לרוב ב-, מתאר את ההפרש בין הארגומנטים של שני גלים.
- קיטוב - קיטוב הוא תופעה המתרחשת בגלי רוחב. קיטוב הגל הוא הכיוון ההפרעה (שהוא, בגל רוחבי, ניצב לכיוון התקדמות הגל). לרוב, משתמשים במושג קיטוב בהקשר של גלים אלקטרומגנטיים. קיטוב עשוי להיות ליניארי, מעגלי (כיוון המשרעת מסתובב באופן מחזורי), אליפטי (המקרה הכללי יותר) או אקראי (לא מקוטב).
משוואת הגלים[עריכת קוד מקור | עריכה]
 ערך מורחב – משוואת הגלים
ערך מורחב – משוואת הגלים
כשמנסים למצוא את הדינמיקה של הרבה סוגי גלים בסיטואציות שונות, בפעמים רבות מגיעים למשוואה משותפת. לכן, משוואה זו זכתה להקרא משוואת הגלים:
זוהי משוואה דיפרנציאלית חלקית, שבה:
- הפונקציה היא השדה הרלוונטי שמשתנה במרחב ובזמן (לדוגמה, שדה חשמלי בגלים אלקטרומגנטיים ושדה לחץ האוויר בגלי קול).
- v היא מהירות התקדמות ההפרעה. היא נקבעת על פי התכונות של התווך הפיזיקלי.
- אופרטורי גזירה: לפלסיאן ונגזרת שנייה לפי הזמן.
באופן כללי, לרוב, המשוואה הזו מתקבלת רק אחרי שעושים מספר קירובים כמו הזנחות של חיכוך, מקדמים שגורמים לנפיצה, תופעות לא ליניאריות וכדומה.
פתרון משוואת הגלים[עריכת קוד מקור | עריכה]
הפתרון הבסיסי של משוואת הגלים שנקרא "גל מישורי" הוא
פתרון זה ניתן להצגה גם כצירוף של סינוסים וקוסינוסים. בנושא זה כדאי לראות את הערך הדן באוסצילטור הרמוני.
כאשר:
- הגודל הוא התדירות הזוויתית של הגל.
- הווקטור הוא וקטור הגל, כיוונו הוא כיוון ההתקדמות של הגל וגודלו עומד ביחס הפוך לאורך הגל, .
- הקשר בין התדירות הזוויתית למספר הגל במקרה זה הוא . במקרה הכללי (כמו בתווך דיאלקטרי, שבו מהירות התקדמות הגל c עשויה להיות תלויה באורך הגל) הקשר הוא לא-ליניארי והפונקציה נקראת יחס נפיצה.
- הפתרון הכללי ביותר של משוואת הגלים הוא סופרפוזיציה של גלים מישוריים עם יחס הנפיצה , כאשר האמפליטודה נקבעת על פי תנאי השפה של הבעיה. אם אין תנאי שפה שמגבילים את הערכים שווקטור הגל k יכול לקבל, אזי הפתרון הכללי נתון על ידי טרנספורם פורייה:
עקרונות פיזיקליים[עריכת קוד מקור | עריכה]
ממשוואת הגלים ניתן להסיק עקרונות פיזיקליים חשובים הנוגעים לטבעם של גלים ולטיב תנועתם. עקרונות אלה אושרו בניסויים וחלקם אף הוסקו באופן אמפירי.
- עקרון פרמה - עקרון הזמן המינימלי. קובע כי בתנועתו בין שתי נקודות, חזית הגל, הנקראת גם קרן, תנוע במסלול בו זמן התנועה הוא הקצר ביותר.
- חוק הויגנס - קובע כי ניתן להתייחס לכל נקודה על גבי חזית הגל כאל מקור של גל נקודתי.
מעקרונות אלו נובעות תכונות ייחודיות המאפיינות תופעות גליות.
תכונות של גלים[עריכת קוד מקור | עריכה]
קיימות מספר צורות התנהגות פיזיקליות אופייניות לגלים. קיומן של תכונות אלו מאפשר לקבוע האם התופעה הנמדדת היא גל. רוב התכונות נובעות מכך שהגל, שהוא פתרון של משוואה דיפרנציאלית חלקית ליניארית, הוא ליניארי, ומחוק הויגנס.
החזרה[עריכת קוד מקור | עריכה]

 ערך מורחב – החזרה (אופטיקה)
ערך מורחב – החזרה (אופטיקה)
החזרה (Reflection) היא כינוי לתופעה שבה חזית גל הנעה בתווך מסוים מגיעה לנקודת מפגש עם תווך אחר ובעקבות כך משנה את כיוונה לכיוון אחר בתווך ממנו הגיעה (וגם את מהירותה). החזרה של גל יכולה להיות באופן מסודר (כגון החזרת אור ממראה) או לא מסודר (כגון החזרת אור מקיר), החזרה קיימת בכל פעם שחזית גל מתווך אחד מגיעה לתווך אחר. על פי חוק סנל, אם זווית הפגיעה היא למעלה מן הזווית הקריטית ישנה החזרה מלאה (כל עוצמת הגל מוחזרת). במקרים אחרים ההחזרה היא חלקית.
שבירה[עריכת קוד מקור | עריכה]
 ערך מורחב – שבירה
ערך מורחב – שבירה
שבירה (Refraction) היא תופעה בה גל העובר מתווך בעל מקדם שבירה אחד אל תווך בעל גורם שבירה שונה ומשנה את כיוונו (וגם את מהירותו). זווית השבירה נקבעת על פי חוק סנל.
תופעות שבירה והחזרה מתוארות ומאופיינות באופן פיזיקלי על ידי תכונה של התווך, הנקראת עכבה (Impedance). העכבה היא היחס בין הכוח הפועל על האמפליטודה למהירות השינוי בה. עבור גלים אלקטרומגנטיים, העכבה היא הכללה של מושג ההתנגדות החשמלית.
התאבכות[עריכת קוד מקור | עריכה]
 ערך מורחב – התאבכות
ערך מורחב – התאבכות
התאבכות היא אולי התופעה המזוהה ביותר עם גלים.

כאשר עוברים מספר גלים דרך אותה נקודה במרחב, האמפליטודה של הגל באותה נקודה תהיה סכום וקטורי (כלומר: כולל התחשבות בכיוון) של האמפליטודות של כל הגלים באותה נקודה. עקרון ההתאבכות הוא מקרה פרטי של סופרפוזיציה - רכיבים ליניאריים המתחברים ביניהם.
באיור לעיל מתוארת התאבכות של שני גלים.
- התאבכות בונה (באיור השמאלי) מתרחשת כאשר כל הגלים מגיעים בשיא ומחזקים זה את זה.
- התאבכות הורסת (באיור הימני) מתרחשת כאשר סכום האמפליטודות שווה לאפס. עבור שני גלים, כאשר שני גלים בעלי אותה אמפליטודה מגיעים במופע הפוך (הפרש מופע של חצי מחזור) מתרחשת התאבכות הורסת שכן גל אחד מגיע בשיא והשני בשפל (שיא שלילי).
עקיפה[עריכת קוד מקור | עריכה]
 ערך מורחב – עקיפה
ערך מורחב – עקיפה
עקיפה (Diffraction) היא תופעה שבה הגל "עוקף" מכשול ונובעת מעקרון הויגנס.
כאשר בין מקור גלים לגלאי מבדיל עצם כלשהו, הגלאי יקלוט חלק מהגל שנפלט מהמקור למרות החסימה בדרך, מכיוון שהגל "עוקף" את המכשול. תופעה זו מתבססת על עקרון הויגנס (ראו נקודת פואסון).
נפיצה[עריכת קוד מקור | עריכה]
 ערך מורחב – נפיצה
ערך מורחב – נפיצה
נפיצה היא תופעה שבה חבורת גלים מתפרקת למרכיביה השונים (גלים בעל תדירות אחת ואורך גל יחיד).
כאשר חבורת גלים המורכבת מאורכי גל שונים עוברת לתווך בעל מקדם שבירה שונה מהתווך ממנו באה (ותלוי באורך הגל), זווית השבירה של כל אורך גל היא שונה. תופעה זו נקראת נפיצה. תופעה נפוצה הנובעת מכך היא הקשת בענן.
התקן שגורם לנפיצה הוא מנסרה, בייחוד מנסרה משולשת. אייזק ניוטון ידוע בניסוייו במנסרות ובכך שהצליח ליצור קשת באופן מלאכותי.
דוגמאות לגלים[עריכת קוד מקור | עריכה]
- תנודות של מיתר מתוח - כאשר פורטים על גיטרה, המיתר מתנודד ונוצר גל עומד, והמשוואה המתארת את תנודת המיתר היא משוואת הגלים האידיאלית (בהתאם לתנאי השפה של קצוות קשורים).
- גלי מים - גל רוחב הנוצר במים כתוצאה ממגע עצם בהם.
- גלי קול - הקול הוא גל אורך של הפרשי לחצים המתפשט בתוך חומר. מהירותו של הקול מושפעת מצפיפות התווך.
- גל אלקטרומגנטי - גל רוחב הנובע משדה חשמלי ושדה מגנטי המשתנים בזמן. גל זה יכול להתפשט גם בריק ומהירותו מושפעת מהחומר בו הוא עובר. גלים אלקטרומגנטיים באורכי גל שונים מכונים בשמות כגון: גלי אור וגלי רדיו.
ראו גם[עריכת קוד מקור | עריכה]
|
עיינו גם בפורטל פורטל הפיזיקה מהווה שער לחובבי הפיזיקה ולמתעניינים בתחום. בין היתר, בפורטל תוכלו למצוא מידע על פיזיקאים חשובים, על ענפי הפיזיקה ועל תאוריות פיזיקליות. |
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- אנימציות של התפשטות גלים בתנאים שונים, ד"ר רובין הוגאן מאוניברסיטת רדינג
- נדב שנרב, צוללות ותורת הגלים, באתר "דיומא", 12 ביולי 2020
- גל, באתר אנציקלופדיה בריטניקה (באנגלית)
| גלים | ||
|---|---|---|
| מאפיינים | משרעת • תדירות • מופע • אורך גל • וקטור גל • מספר גל • מהירות פאזה • מהירות חבורה • קיטוב | 
|
| תופעות | החזרה • העברה • שבירה • התאבכות • עקיפה • נפיצה • בליעה | |
| מושגים | גל עומד • אפנון • חבילת גלים • תווך • מתנד הרמוני • תהודה • אפקט דופלר | |
| אנליזה | משוואת הגלים • משוואת הלמהולץ • עקרון הויגנס • עקרון פרמה • חוקי פרנל | |
| סוגי גלים | גל מישורי • גל כדורי • גל רוחב • גל אורך • פולס • קרינה אלקטרומגנטית • גל קול • גל (מים) • פונקציית גל | |