רשת פייסטל

בקריפטוגרפיה, רשת פייסטל (או מבנה פייסטל) היא שיטה גנרית לבניית פונקציה פנימית איטרטיבית של צופן בלוקים הקרויה על שם ממציאה, המדען הגרמני-אמריקאי הורסט פייסטל. רשת פייסטל מחלקת את הטקסט הגלוי לשני חצאים, ימין ושמאל. בכל איטרציה מופעלת הפונקציה הפנימית על צד אחד כאשר פלט הפונקציה משמש להצפנת הצד השני באמצעות פעולת או-אקסקלוסיבי (XOR) ואילו החצי הראשון נותר ללא שינוי. באיטרציה הבאה מחליפים בין הצדדים כך שהפלט מהצד הימני הופך להיות הקלט לצד השמאלי ולהפך.

הרעיון של פייסטל הוא ליצור תמורה פסאודו-אקראית (בקיצור PRP) מפונקציה פסאודו-אקראית שאינה בהכרח הפיכה (בקיצור PRF), שזו תכונה בסיסית הנדרשת מכל צופן בלוקים אחרת פענוח לא יהיה אפשרי תמיד. המבנה הסימטרי גורם לכך שפונקציות ההצפנה והפענוח מבוצעות באופן זהה בהחלפת סדר הזנת המפתחות בלבד. מבנה זה מקטין את גודל היישום של הצופן במיוחד בחומרה, היות שאין צורך ליישם את פונקציות ההצפנה והפענוח בנפרד. רשת פייסטל הוכחה כבטוחה, היא פופולרית ביותר ונכללת בצפנים מודרניים רבים, בהם: DES, Blowfish, KASUMI, Twofish, 3DES, Tiny, RC5 ו-TEA.

היסטוריה

רשת פייסטל הופיעה לראשונה בצופן לוציפר שפותח במשותף על ידי הורסט פייסטל ודון קופרשמידט במסגרת עבודתם ב-IBM. השימוש בבנייה הפך נפוץ לאחר שהממשל הפדרלי של ארצות הברית אימץ את תקן ההצפנה DES שהתבסס על לוציפר.

כאמור, צפנים רבים הם בעלי מבנה פייסטל. עובדה זו הובילה לכך שהקהילה המדעית השקיעה מאמץ אקדמי רב בניתוח תכונות המבנה. בעבודתם משנת 1988 הוכיחו מיכאל לובי וצ'ארלס רקופף שאם פונקציית השלב מתנהגת בצורה פסבדו-אקראית תחת מפתח ההצפנה אזי שילובה בתוך רשת פייסטל יניב תמורה פסאודו-אקראית לאחר 3 איטרציות ותמורה פסאודו-אקראית חזקה לאחר 4 איטרציות. אחד היתרונות של רשת פייסטל על-פני רשת החלפה-תמורה הוא שפונקציית השלב אינה חייבת להיות הפיכה.

פרטי הבנייה

באופן כללי, מבנה פייסטל ממפה טקסט גלוי באורך $2\cdot t$ סיביות המחולק לשניים $(L_{0},R_{0})$ בהתאמה, לטקסט מוצפן $(R_{n},L_{n})$ באורך $2\cdot t$ בהתאמה, באמצעות $n$ מפתחות הצפנה $k_{1},...,k_{n}$ בתהליך $n$ שלבי. בכל שלב, מחצית הקלט האחת מוזנת לפונקציה $f_{i}$ שבתורה מפיקה מהקלט ומפתח ההצפנה המתאים $k_{i}$ פלט פסאודו-אקראי המשמש כמפתח להצפנת מחצית הקלט השנייה באמצעות XOR ואז הן מחליפות מקומות. אפשר לראות שבכל שלב היות ש-XOR הפיכה, אם חוזרים על אותה הפעולה עם המפתח המתאים מתקבל הקלט המקורי. מכאן שהפענוח יכול להתבצע באופן דומה אך בסדר הפוך של הסבבים ועם החלק המתאים של המפתח.

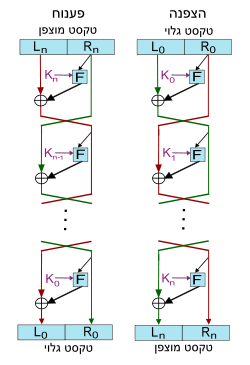
ביתר פירוט תהי $F$ פונקציית שלב ויהיו $K_{0},K_{1},\ldots ,K_{n}$ מפתחות הצפנה, הנקראים תת-מפתחות, המתאימים לאיטרציות $0,1,\ldots ,n$ בהתאמה. הבנייה עובדת באופן הבא:

1. הבנייה מחלקת את הטקסט הגלוי לשני חלקים שווים $L_{0}$, $R_{0}$.
2. עבור כל שלב $i=0,1,\ldots ,n$ מבצעים:

$L_{i+1}=R_{i}\,$

$R_{i+1}=L_{i}\oplus {\rm {F}}(R_{i},K_{i})$.

• הטקסט המוצפן הוא:

$\ (R_{n},L_{n})$

פענוח הצופן נעשה באופן דומה בסדר איטרציות הפוך $i=n,n-1,\ldots ,0$

$R_{i}=L_{i+1}\,$

$L_{i}=R_{i+1}\oplus {\rm {F}}(L_{i+1},K_{i})$.

• כך שבסוף התהליך מתקבל שוב הטקסט הגלוי:

$\ (R_{0},L_{0})$

ביטחון

אם מסמנים את רשת פייסטל ב-$r$ סבבים:

$(L_{r},R_{r})={\text{Feistel}}_{f_{1},...,f_{r}}(L_{0},R_{0})$

כאשר $f_{1},...,f_{r}$ הן $r$ פונקציות שונות (לא בהכרח הפיכות) הממפות מחרוזת באורך $2n$ סיביות למחרוזת באורך $2n$ סיביות. אפשר לראות שעבור כל ערך $r$ הרשת ${\text{Feistel}}$ היא תמורה הפיכה ויעילה ללא תלות בפונקציות הפנימיות. ביתר פירוט אם $F$ היא פונקציה פסאודו-אקראית אז רשת פייסטל עם סבב בודד $F^{(1)}$ המוגדרת כ:

$F_{k}^{(1)}(x)={\text{Feistel}}_{F_{k}}(x)$

היא פרמוטציה עם מפתח מעל $\{0,1\}^{2n}$ כאשר $k\in \{0,1\}^{n}$, אך היא אינה פסאודו אקראית כי $n$ הסיביות הראשונות של הפלט ($L_{1}$) שוות ל-$n$ הסיביות האחרונות של הקלט ($R_{0}$) ללא תלות במפתח. מעבר לבעיה שחלק מהטקסט המקורי פשוט לא הוצפן כלל ונותר במצבו הגלוי, עובדה זו כשלעצמה מצביעה בבירור שהפונקציה אינה פסאודו אקראית כי מקרה כזה שבו רק מחצית הקלט השתנתה, יכול להתרחש בסבירות מאוד מאוד נמוכה אילו היה מדובר בפונקציה אקראית אמיתית.

יתרה מזו, במקרה כזה קל לנחש את המפתח. למשל במקרה של DES עם סבב אחד, התוצאה תהיה $L_{1}=R_{0}$ וכן $R_{1}=L_{0}\oplus F_{k}(R_{0})$, במצב כזה הקלט והפלט של הפונקציה הפנימית ידוע. כלומר אנחנו יודעים ש-$F_{k}(R_{0})=R_{1}\oplus L_{0}$. לכן אם מבצעים את התמורה ההפוכה של $P$ (ב-DES התמורה $P$ רק מבצעת "סידור מחדש" של הסיביות לפי טבלה קבועה), על $R_{1}\oplus L_{0}$ מתקבלים ערכי ביניים שהם תוצאה של תיבות ההחלפה (S-box), כל תיבת החלפה מקבלת שש סיביות ומחזירה ארבע. כזכור הקלט לתיבות ההחלפה הוא XOR של תיבת ההרחבה $E$ עם חלק מהמפתח במקרה זה המפתח היחידי $k$ וכל חלק משפיע על תיבת החלפה אחרת. כך שאפשר לדעת אם ניחוש של 6 סיביות הצליח פשוט על ידי בדיקה שקלט ופלט הפונקציה הפנימית מתאים בפוזיציות הללו. היות שתיבות ההחלפה מכווצות את הקלט, עבור כל 6 סיביות מפתח ישנם רק ארבעה פלטים אפשריים. יוצא איפה שאפשר לצמצם את החיפוש בכוח גס של המפתח מ-$2^{48}$ ל-$4^{48/6}=4^{8}$ שזה $2^{16}$ ניסיונות (במחשב רגיל חיפוש כזה לא לוקח יותר ממספר מילי שניות). היות שההתקפה האמורה הסתמכה על מבנה הפונקציה הפנימית המשמעות היא שבמקרה של DES רשת פייסטל עם סבב אחד לא נחשבת בטוחה.

רשת פייסטל בשני סבבים

רשת פייסטל בשני סבבים $F^{(2)}$ כדלהלן:

$F_{k_{1},k_{2}}^{(2)}(x)={\text{Feistel}}_{F_{k_{1}},F_{k_{2}}}(x)$

כאשר $k_{1}$ ו-$k_{2}$ הם שני מפתחות נפרדים ובלתי תלויים זה בזה, עדיין אינה פסאודו אקראית משום שאפשר לבצע את הטריק הבא: מצפינים שני מסרים כאשר $n$ הסיביות האחרונות שלהם זהות, לדוגמה $x_{1}=L_{0}R_{0}$, $x_{2}=L_{0}^{*}R_{0}$ ומקבלים מהם שני טקסטים מוצפנים $c_{1}=(L_{2}R_{2})$ ו-$c_{2}=(L_{2}^{*}R_{2}^{*})$ בהתאמה. ה-XOR של המחצית הראשונה של $c_{1}$ עם המחצית הראשונה של $c_{2}$ דהיינו $L_{2}\oplus L_{2}^{*}$ שווה ל-$L_{0}\oplus L_{0}^{*}$. לכן התקפת הבחנה פשוטה יכולה לשבור את האלגוריתם. אם השוויון האמור מתקיים המתקיף מחזיר '1' אחרת '0'. הסיבה לכך נובעת מהעובדה שהמפתחות לא הספיקו להשפיע על כל הפלט במידה שווה בשל מספר הסבבים המועט. לתופעה זו קוראים אפקט מפולת. כלומר השאיפה היא שלאחר מספר ראוי של סבבים עם מפתחות שונים, כמעט כל סיביות הפלט יושפעו במידה שווה במקרה הממוצע ולכן התקפה כזו לא תהיה אפשרית.

ניחוש המפתח קשה יותר אך עדיין בר ביצוע. למשל במקרה של DES אפשר לראות שעם שני סבבים אפשר לבצע התקפה דומה ל-DES בסבב אחד המתוארת לעיל כי הקלט והפלט של הפונקציה הפנימית בשני הסבבים ידוע. כלומר אפשר לנחש את המפתחות בזמן של $2\cdot 2^{16}$ אפילו אם המפתחות בלתי תלויים זה בזה כלל. אף על פי שתהליך הרחבת המפתח של DES למעשה משתמש במפתח המאסטר בשינויים קלים כדי להכין את מפתחות הסבבים כך שסיביות מסוימות של $k_{1}$ ו-$k_{2}$ למעשה זהות, דבר שיכול לעזור להתקפה.

רשת פייסטל בשלושה סבבים

רשת פייסטל בשלושה סבבים $F^{(3)}$ המוגדרת כדלהלן:

$F_{k_{1},k_{2},k_{3}}^{(3)}(x)={\text{Feistel}}_{F_{k_{1}},F_{k_{2}},F_{k_{3}}}(x)$

באופן מפתיע כן נחשבת פסאודו אקראית בהנחה שמשתמשים בשלושה מפתחות נפרדים והפונקציה הפנימית היא פסאודו-אקראית. אך היא אינה פסאודו-אקראית חזקה.

ניחוש המפתח במקרה של DES עם שלושה סבבים קשה יותר. אפשר לראות שבמצב זה אין בידי המתקיף מידע מלא על קלט/פלט הפונקציה הפנימית בכל הסבבים כמו בדוגמאות הקודמות ולכן כוח גס ישיר אינו אפשרי כיוון שחסר למתקיף מידע האם הניחוש שלו הצליח. לדוגמה בסבב השני הפלט הוא $L_{1}\oplus R_{2}$ כאשר שני הערכים האמורים ידועים אבל הקלט $R_{1}$ נותר בלתי ידוע. מצד שני אנחנו יודעים ש-$R_{1}=L_{0}\oplus F_{k_{2}}(R_{0})$ וכן $R_{1}=R_{3}\oplus F_{k_{3}}(R_{2})$ אבל הפלט של $F_{K_{1}}$ ו-$F_{k_{3}}$ לא ידוע.

אבל במקום להסתמך על ניחוש הקלט והפלט המלאים של הפונקציה הפנימית בכל הסבבים, המתקיף יכול להתמקד ביחס שבין החלקים השונים של הקלט שמקצתם ידוע. היות שהפלט בסבב הראשון הוא $L_{0}\oplus R_{1}=L_{0}\oplus L_{2}$ והפלט בסבב השלישי הוא $L_{2}\oplus R_{3}$ יוצא ש-XOR של הפלט מהסבב הראשון עם הפלט מהסבב השני שווה ל-

$(L_{0}\oplus L_{2})\oplus (L_{2}\oplus R_{3})=L_{0}\oplus R_{3}$

כאשר הערך האחרון ידוע. על בסיס נתון זה והעובדה שתהליך הרחבת המפתח של DES מחלק את המפתח לשני חצאים, כל חצי משפיע רק על החצי המתאים מהקלט (רק ארבע תיבות החלפה), ואם נוסיף לכך את העובדה שהתמורה המפזרת ידועה גם היא כך שאפשר לדעת כל סיבית מהיכן הגיעה, יוצא שאפשר לבצע התקפה לניחוש חצי מהמפתח בזמן של $2^{28}$ זאת בתנאי שיש דרך לדעת האם ניחוש הצליח. היות שהקלט לסבב הראשון ידוע, אפשר לנחש חצי מהמפתח לחשב את ארבע תיבות ההחלפה המושפעות מחצי זה, באותה מידה לבדוק להיכן הסיביות עברו בעקבות הפיזור ובכך לקבל מחצית מפלט הסבב הראשון. באותה דרך אפשר לחשב את אותן הפוזיציות בפלט הסבב השלישי (כזכור הקלט לסבב השלישי ידוע). עם מידע זה אפשר לוודא שהניחוש נכון על ידי השוויון המתואר לעיל. כמובן שניחוש נכון אינו מעיד בהכרח שנמצא המפתח הנכון אלא רק בהסתברות של $2^{-16}$ כלומר מתוך $2^{28}$ מפתחות אפשריים נשארים עם $2^{28}/2^{16}=2^{12}$ אפשרויות תקפות עבור חצי מפתח ו-$2^{24}$ עבור המפתח כולו. כך שאם בידי המתקיף מספר זוגות קלט/פלט של DES הוא יכול לנחש את המפתח במלואו בזמן כולל של $2\cdot 2^{28}+2^{24}<2^{30}$ ועם זיכרון בסדר גודל של $2\cdot 2^{12}$. התקפה בסיבוכיות כזו ניתנת לביצוע כיום על מחשב אישי בזמן מאוד קצר.

ההתקפה המתוארת הסתמכה על המבנה הפנימי של הפונקציה הפסאודו-אקראית והיא רלוונטית רק לגבי DES. אין הדבר מעיד בהכרח על כך שרשת פייסטל בשלושה סבבים אינה בטוחה, כל עוד הפונקציה הפנימית נחשבת פסאודו אקראית בטוחה.

רשת פייסטל בארבעה סבבים

הוכח שאם מוסיפים סבב רביעי מתקבלת תמורה פסאודו-אקראית חזקה, כדלהלן:

קלט: מפתח $k\in \{0,1\}^{4n}$ שמתחלק לארבעה מפתחות $k_{1},k_{2},k_{3},k_{4}$ כאשר $|k_{i}|=n$ וקלט $x\in \{0,1\}^{2n}$ שמחולק ל-$L_{0},R_{0}$ כאשר $|L_{0}|=|R_{0}|=n$ וכן פונקציה פסאודו-אקראית כלשהי $F$ ש"מערבבת" הקלט באורך $n$ יחד עם המפתח ומחזירה פלט פסאודו-אקראי באורך $n$ באופן כזה שהתוצאה נראית אקראית.

1. מחשבים את $L_{1}=R_{0}$ וכן $R_{1}=L_{0}\oplus F_{k_{1}}(R_{0})$

2. מחשבים את $L_{2}=R_{1}$ וכן $R_{2}=L_{1}\oplus F_{k_{2}}(R_{1})$

3. מחשבים את $L_{3}=R_{2}$ וכן $R_{3}=L_{2}\oplus F_{k_{3}}(R_{2})$

4. מחשבים את $L_{4}=R_{3}$ וכן $R_{4}=L_{3}\oplus F_{k_{4}}(R_{3})$

הפלט הוא $(L_{4},R_{4})$.

הוכח שהמבנה המתואר הוא פונקציה פסאודו אקראית חזקה והיא הנפוצה ביותר בצפנים מודרניים. בכל אופן קיימת קריפטואנליזת "התקפת הבחנה גנרית" נגד מבנה פייסטל עד שבעה סבבים בסיבוכיות של $2^{2n}$ כאשר $n$ מתייחס לגודל מחצית הקלט בסיביות.

רשת פייסטל כללית

צפנים מודרניים מגיעים לפעמים עם רשת פייסטל בסגנון שונה מרשת פייסטל הקלאסית שהגיעה עם DES. היא נקראת רשת פייסטל כללית (General Feistel Network) בקיצור GFN שהיא מעין הכללה של מבנה פייסטל בכמה שינויים. קיימים כמה סוגים ביניהם:

• רשת פייסטל כללית בלתי מאוזנת (Unbalanced).
• רשת פייסטל כללית מתחלפת (Alternating).
• רשת פייסטל כללית מסוג 1 (Type 1).
• רשת פייסטל כללית מסוג 2 (Type 2).
• רשת פייסטל כללית מסוג 3 (Type 3).

בין הצפנים המודרניים שמיישמים רשת פייסטל בסגנון שונה מ-DES הם: RC6 ו-CLEFIA המיישמים רשת פייסטל מסוג 2, MARS המיישם רשת פייסטל מסוג 3, CAST הבנוי מרשת פייסטל מסוג 1 ועוד רבים. מהיבט תאורטי הביטחון המוכח של רשת פייסטל הקלאסית החל עם עבודתם של לובי וראקוף, בהנחה ש-$r$ הפונקציות הפנימיות נבחרו באופן אקראי ובלתי תלוי. הנושא נחקר על ידי רבים אחרים כמו מאורר, נאור וריינגולד, ואודני, פיטרזק ופטרין. האחרון הוכיח שרשת פייסטל הקלאסית עם שישה סבבים מספיק טובה נגד התקפת מוצפן נבחר עם $2^{n(1-\epsilon )}$ שאילתות עבור כל $\epsilon >0$. לגבי הכללה של רשת פייסטל אין ידע תאורטי נרחב כמו בקלאסית.

רשת פייסטל בלתי מאוזנת

רשת פייסטל כללית בלתי מאוזנת

רשת פייסטל כללית לא מאוזנת הנקראת בקיצור UFN היא מבנה דומה לרשת פייסטל הקלאסית הכולל סדרה של $r$ פונקציות בהן חלק מבלוק הקלט משמש קלט לפונקציה המצפינה את יתרת הבלוק ואז הם מתחלפים ביניהם. ההבדל הוא שבניגוד לקלאסית ברשת לא מאוזנת שני החלקים אינם בגודל שווה.

בניסוח רשמי, יהיו הפרמטרים $n$ ו-$m$ שלמים חיוביים גדולים מאפס ותהי הפונקציה הפסאודו-אקראית $F:\{0,1\}^{n}\rightarrow \{0,1\}^{m}$ כאשר $m>n$ או $m<n$ (במקרה ש-$n=m$ מתקבלת רשת פייסטל רגילה). מגדירים את הפרמוטציה $\Psi _{F}:\{0,1\}^{m+n}\rightarrow \{0,1\}^{m+n}$ על ידי:

${\boldsymbol {\Psi _{F}(A,B)=(B,A\oplus F(B))}}$

כאשר $|A|=m$ סיביות ו-$|B|=n$ סיביות והסימן $\oplus$ הוא XOR. הסמל $\Psi$ מייצג את רשת פייסטל עם פונקציית הסבב הפנימית $F$ המבוצעת $r$ פעמים עם $r$ מפתחות שונים. מרחב המפתח הוא $(m+n)r$ סיביות. דרך אחרת להציג זאת היא ההרכבה:

$\Psi _{F_{1}}\circ \Psi _{F_{2}}\circ \cdots \circ \Psi _{F_{r}}$ (המחשה של המבנה מובאת בתרשים משמאל).

אפשר לחלק עוד את רשת פייסטל בלתי מאוזנת לשתי שיטות. אם $m>n$ זו היא רשת פייסטל בלתי מאוזנת מסוג source heavy אחרת אם $m<n$ היא מסוג target heavy. אם $b$ הוא gcd (מחלק מרבי משותף) של $m$ ו-$n$ אז הפונקציה הפנימית $F$ מורכבת מאוסף של $2^{k}$ פונקציות הממפות מספר באורך $m$ סיביות למספר באורך $n$ סיביות ולהפך. או $m/b$ תת-בלוקים ל-$n/b$ תת-בלוקים.

רשת פייסטל מתחלפת

רשת פייסטל כללית מתחלפת

רשת פייסטל מתחלפת (Alternating Feistel Network) בקיצור AFN היא רשת פייסטל שבה משתמשים בשתי פונקציות פנימיות המופעלות לסירוגין.

אם $m$ ו-$n$ הם שלמים חיוביים כאשר $m\geq n$, רשת פייסטל מתחלפת היא רשת פייסטל בלתי מאוזנת הכוללת $r$ סבבים שבהם כל סבב אי זוגי הוא מהצורה ${\text{F}}(m,n)$ (סבב מכווץ) וכל סבב זוגי הוא מהצורה ${\text{F'}}(n,m)$ (סבב מרחיב). ההנחה היא ש-$r$ זוגי.

רשת פייסטל כללית מסוג 1

רשת פייסטל כללית מסוג 1

בניגוד לרשת פייסטל הקלאסית שמחלקת את בלוק הקלט לשני חצאים ימין ושמאל בהתאמה, רשת פייסטל כללית מסוג 1, 2 או 3 היא רשת פייסטל הפועלת במספר ערוצים גדול יותר (בלוק הקלט מחולק למספר חלקים גדול או שווה לשניים), עם פונקציה פנימית אחת, שתים או שלוש בהתאמה. הפונקציות הפנימיות מופעלות בכל סבב על חלק מהערוצים לסירוגין ולאחר מכן הם מחליפים מקומות לפי סדר מסוים. בניסוח רשמי, יהיו הפרמטרים $k\geq 2$ וכן $n\geq 1$ שני שלמים חיוביים (אם $k=2$ מתקבלת רשת פייסטל רגילה). תהי $F:\{0,1\}^{n}\rightarrow \{0,1\}^{n}$ פונקציה חד-כיוונית עבור התמורה $\Psi _{F}:\{0,1\}^{n}\rightarrow \{0,1\}^{n}$. רשת פייסטל כללית מסוג 1 מוגדרת בניסוח רשמי:

$\Psi _{F}(B_{1},...,B_{k})=(B_{2}\oplus F(B_{1}),B_{3},...,B_{k},B_{1})$

התמורה פועלת על $k$ ערוצים שהם המילים $B_{i}$, כל אחד מהם באורך $n$ סיביות.

רשת פייסטל כללית מסוג 2

רשת פייסטל כללית מסוג 2

רשת פייסטל כללית מסוג 2. יהיו הפרמטרים $k\geq 2$ וכן $n\geq 1$ שני שלמים חיוביים. יהיו $k/2$ פונקציות חד-כיווניות $f_{i}:\{0,1\}^{n}\rightarrow \{0,1\}^{n}$ עבור כל $i\leq k/2$. תהי $F=(f_{1},...,f_{k/2})$ המאגדת בתוכה את הפונקציות האמורות עבור התמורה $\Psi _{F}:\{0,1\}^{kn}\rightarrow \{0,1\}^{kn}$ המוגדרת כך:

$\Psi _{F}(B_{1},...,B_{k})=(B_{2}\oplus f_{1}(B_{1}),B_{3},B_{4}\oplus f_{2}(B_{3}),B_{5},...,B_{k}\oplus f_{k/2}(B_{k-1}),B_{1})$

כאשר $B_{i}$ הן מילים באורך $n$ סיביות.

רשת פייסטל כללית מסוג 3

רשת פייסטל כללית מסוג 3

רשת פייסטל מסוג 3. יהיו הפרמטרים $k\geq 3$ וכן $n\geq 1$ שני שלמים חיוביים. יהיו $k-1$ פונקציות חד-כיווניות $f_{i}:\{0,1\}^{n}\rightarrow \{0,1\}^{n}$ עבור כל $i\leq k-1$. תהי $F=(f_{1},...,f_{k-1})$ פונקציה המאגדת את כל הפונקציות החד-כיווניות עבור התמורה $\Psi _{F}:\{0,1\}^{kn}\rightarrow \{0,1\}^{kn}$ המוגדרת כך:

$\Psi _{F}(B_{1},...,B_{k})=(B_{2}\oplus f_{1}(B_{1}),B_{3}\oplus f_{2}(B_{2}),...,B_{k}\oplus f_{k-1}(B_{k-1}),B_{1})$

כאשר $|B_{i}|=n$.

ראו גם

• רשת החלפה-תמורה