צופן קיסר
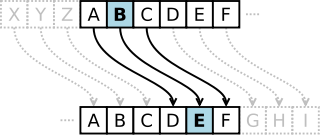
בתחום הקריפטוגרפיה, צופן קיסר, הידוע גם כצופן היסט, קוד קיסר או היסט קיסר או הסטה קיסרית, הוא אחד הצפנים הפשוטים והידועים בעולם ההצפנה. זהו סוג של צופן החלפה שבו כל אות בטקסט מוחלפת על ידי אות הנמצאת בהיסט קבוע כלשהו ממנה באלף-בית. למשל אם נקבע את ההיסט להיות 3, האות A תוחלף באות D, האות B תוחלף באות E וכך הלאה. הכינוי קיסר נובע מכך שיוליוס קיסר נהג להשתמש בצופן על מנת לתקשר עם מפקדיו.
צעד ההצפנה המבוצע על יד הצופן משולב במנגנונים יותר מורכבים, כמו צופן ויז'נר. כמו כל צופן החלפה אלפביתי, צופן קיסר ניתן לפיענוח בקלות ואינו מספק כמעט שום הגנה על אמצעי התקשורת.
היסטוריה ושימושים[עריכת קוד מקור | עריכה]

צופן קיסר מכונה כך על שם יוליוס קיסר, שלפי דבריו של סווטוניוס, עשה בו שימוש עם היסט של 3 כדי להסתיר את תוכנן של הודעות צבאיות :
"אם היה לו מסר מסווג, הוא רשם אותו בקוד, כלומר, על ידי שינוי סדר האותיות של האלף-בית, כך שאף מילה לא הייתה מובנת. אם מישהו חשק לפענח את ההודעות ולהבין את משמעותן, היה עליו להחליף אותיות."
— סווטוניוס, יוליוס האלוהי, 56.6
לא ברור עד כמה יעיל היה צופן קיסר באותה תקופה, אולם סביר שהצופן היה יחסית בטוח משום שמעט מאויביו היו משכילים ובוודאי שלא בעלי יכולת לחשוב על שיטת פענוח. בהנחה שמישהו יכול לקרוא את ההודעה, אין עדות לשיטה כלשהי לפתרון צפני החלפה פשוטים. העדות המוקדמת ביותר היא מהמאה ה-9 לספירה בעולם הערבי עם פיתוח שיטת ניתוח התדירות.
במאה ה-19, היה אזור בעיתונים ששימש לעיתים להחלפת הודעות מוצפנות בצפנים פשוטים. דייוויד קאהן מתאר מקרים של זוגות אוהבים שהתכתבו תוך שימוש בצופן קיסר בעיתון הטיימס. אפילו בתקופת מלחמת העולם הראשונה, צבא האימפריה הרוסית עדיין השתמש בצופן קיסר, כתחליף לצפנים מורכבים שהיו קשים יותר להטמעה בקרב החיילים; מפענחים אוסטרים וגרמנים לא התקשו לפענח את הודעותיהם.
צופן קיסר מצוי לעיתים בצעצועי ילדים כמו טבעות הצפנה. היסט קיסר של 13 מבוצע באלגוריתם ה-ROT13, שיטה פשוטה להסתרת טקסט שמשמשת לעיתים בפורומים באינטרנט אך לא משמשת כשיטת הצפנה.
צופן ויז'נר עושה שימוש בצופן קיסר עם היסט שונה בכל מקום בטקסט. ערך ההיסט נקבע באמצעות מילה חוזרת. אם מילה ארוכה מספיק ונבחרת באקראי אז זהו צופן פנקס חד פעמי, שאינו ניתן לפענוח אם המשתמש שומר על מילת המפתח בסוד. מילות מפתח קצרות מההודעה, חושפות דפוס ציקלי שעשוי להתגלות עם גרסה סטטיסטית מתקדמת של ניתוח תדרים.
שימוש יוצא דופן בצופן הוא בקלף המזוזה מתקופת הגאונים, בו נכתב, בשיטת הסטה של מקום אחד שמאלה, "כוזו במוכסז כוזו"[1] ("ה' אלוהינו ה'") כדי שלא לכתוב את השם המפורש.
פענוח הצופן[עריכת קוד מקור | עריכה]
| היסט הפענוח |
הטקסט הנתון |
|---|---|
| 0 | exxegoexsrgi |
| 1 | dwwdfndwrqfh |
| 2 | cvvcemcvqpeg |
| 3 | buubdlbupodf |
| 4 | attackatonce |
| 5 | zsszbjzsnmbd |
| 6 | yrryaiyrmlac |
| ... | |
| 23 | haahjrhavujl |
| 24 | gzzgiqgzutik |
| 25 | fyyfhpfytshj |
צופן קיסר ניתן בקלות לפענוח גם אם ברשותנו רק הטקסט המוצפן ללא המפתח. שני מקרים באים בחשבון:
- המפענח יודע (או מנחש) שנעשה שימוש בצופן החלפה כלשהו מבלי שהוא יודע בהכרח שמדובר בצופן מסוג קיסר.
- המפענח יודע שנעשה שימוש בצופן קיסר אולם אינו יודע את ערך ההיסט.
במקרה הראשון, הקידוד יכול להתפענח תוך שימוש בשיטות כלליות כמו בצופן החלפה רגיל. שיטה כמו ניתוח תדרי או מילים נפוצות. בעת הפענוח, המפענח אמור לזהות דפוס חוזר כלשהו בפתרון ולהסיק שבעת הקידוד נעשה שימוש בצופן קיסר.
במקרה השני, הפענוח אף יותר ישיר. מאחר שיש רק מספר מוגבל של היסטים (לפי מספר האותיות בשפה), ניתן לבחון כל היסט בתורו בהתקפת כוח גס. דרך אחת לבצע זאת היא לנהל טבלה של כל ההיסטים האפשריים. הדוגמה ממחישה זאת עבור הטקסט המוצפן "EXXEGOEXSRGI"; הטקסט המקורי מיד מזוהה בעין כאשר מבצעים היסט של 4. דרך אחרת להבין את השיטה היא לדמיין שתחת כל אות בטקסט המוצפן, כל האלף-בית רשום בהיפוך החל מאותה אות. ניתן לשפר את שיטת ההתקפה אם משתמשים ברצועות שעליהן רשום האלף בית מהסוף להתחלה. הרצועות אז מיושרות כדי ליצור את הטקסט המוצפן בשורה אחת, ואת טקסט המקור בשורה אחרת.
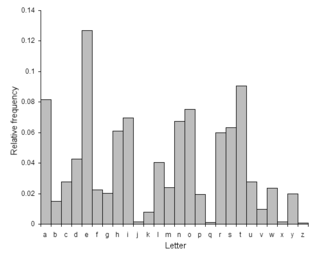
גישת כוח גס שונה כרוכה לזווג בין פילוגי התדירויות של האותיות. על ידי שרטוט גרף של תדירות הופעת האותיות בטקסט המוצפן ותוך ידיעת הפילוג הצפוי של האותיות בשפת המקור של הטקסט המקורי, ניתן בקלות לזהות את ערך ההיסט על ידי בחינה של תכונות הגרף. זהו ניתוח תדירות. למשל בשפה האנגלית התדירויות של האותיות E, T, (בדרך כלל מופיעות הכי הרבה) ו Q, Z (מופיעות הכי מעט) שונות לחלוטין. מחשבים יכולים לבצע סוג כזה של בדיקה על ידי השוואה של פילוג התדירויות הנתון לפילוג הצפוי בשפה; למשל ניתן לעשות שימוש במבחני מבחן כי בריבוע.
לטקסט בשפה טבעית, יהיה פענוח יחיד. אולם לטקסטים קצרים במיוחד ייתכנו מספר מועמדים. למשל, הטקסט המוצפן MPQY עשוי להיות מפוענח כ "aden" או כ "know" (בהנחה שטקסט המקור הוא באנגלית); באופן דומה "ALIIP" הופך ל "dolls" או למילה "wheel";
במקרה השני ניתן גם להשתמש בפענוח תדירויות גס, וניתן לנסות רק מספר קטן עוד יותר של אפשרויות- פענוח אות אחת במקרה הזה הוא פענוח כל הצופן. גם אם מספר אותיות מפוענחות ונראה שהן מסודרות על פי צופן קיסר, ניתן להסיק שכל הצופן הוא צופן קיסר ולבדוק אם מתקבלת תוצאה הגיונית.
ביצוע חוזר של הצפנות ופענוחים לא מספק מידה נוספת של אבטחה. ההסבר המתמטי לכך הוא שההצפנה יוצרת תחת מפתחות שונים חבורה.
דוגמה[עריכת קוד מקור | עריכה]
ההתמרה שמבצע הצופן מומחשת בפשטות כאשר מישרים שתי קבוצות של אלף-בית; האלף-בית של הצופן הוא האלף בית של המקור מוסט במספר מיקומים ימינה או שמאלה. למשל בדוגמה שלהלן נתון צופן קיסר שבו מבוצעת הסטה ימינה של 3 מקומות. פרמטר ההיסט, שכאן הוא נקבע להיות 3, משמש כמפתח הצופן:
מקור: abcdefghijklmnopqrstuvwxyz מוצפן: DEFGHIJKLMNOPQRSTUVWXYZABC
כדי לקודד הודעה, יש לבחון כל אות באלף בית של המקור לעיל ולהחליפה באות שמתחתיה באלף בית המוצפן. כדי לפענח יש לבצע את הפעולה ההפוכה בדיוק. להלן שורת הודעה לדוגמה שמקודדת לפי האלף בית שלעיל :
מקור: the quick brown fox jumps over the lazy dog מוצפן: WKH TXLFN EURZQ IRA MXPSV RYHU WKH ODCB GRJ
ההצפנה יכולה להיות מיוצגת גם על ידי שימוש בחשבון מודולרי. בשיטה זו, ראשית יש להתמיר את האותיות למספרים לפי,A = 0, B = 1,..., Z = 25. הצפנה של אות תוך שימוש בהיסט n יכולה להיות מתוארת מתמטית באופן הבא,
פענוח מבוצע באופן דומה רק על ידי החלפת סימן,
ההחלפה נותרת בעינה לאורך כל ההודעה, כך שהצופן מסווג כצופן מונואלפביתי, בניגוד להחלפה פוליאלפביתית.
מקורות[עריכת קוד מקור | עריכה]
- David Kahn, The Codebreakers — The Story of Secret Writing, 1967. ISBN 0-684-83130-9.
- F.L. Bauer, Decrypted Secrets, 2nd edition, 2000, Springer. ISBN 3-540-66871-3.
- Chris Savarese and Brian Hart, The Caesar Cipher 1999 Caesar Cipher, web.archive.org, 2009-04-17.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- תוכנה לקידוד טקסט התוכנה מכילה שיטת התקפת מילון כדי לפענח את הטקסט באופן אוטומאטי
- מקודד היסט קיסר בפורמט Excel מאפשר לראות את כל 25 האפשרויות בו זמנית
- מקודד online לקוד קיסר
- צופן קיסר, באתר MathWorld (באנגלית)
- היסט קיסר
- מדריך למתחילים בנושא הצפנה
- מקורות היסטוריים לשימוש בצופן קיסר
- JavaScript Shift Cipher Encryptor/Decryptor
- Code Cracker (אורכב 24.09.2005 בארכיון Wayback Machine) Cracks many classic encryption codes including Caesar cipher, trying all permutations
- מקודד online בשיטת קיסר(הקישור אינו פעיל)
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ דוד לאו, "כוזו במוכסז כוזו" במזוזה, באתר "מורשת", כ"ח בשבט התשס"ו


