אלכסון
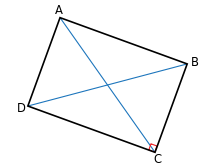
בגאומטריה, אֲלַכְסוֹן (מיוונית λοξόν, נטוי) הוא קטע המחבר בין שני קודקודים של מצולע שאינם נמצאים על צלע אחת. במשולש אין אלכסונים כלל, במרובע יש שני אלכסונים, ובמחומש יש חמישה אלכסונים.
כאשר במצולע יש n קודקודים, מכל קודקוד ניתן למתוח אלכסונים לכל הקודקודים, מלבד אל עצמו ואל שני הקודקודים הסמוכים אליו, ובסך הכול ניתן למתוח n − 3) × n) אלכסונים. בדרך זו ספרנו כל אלכסון פעמיים (מכיוון שאלכסון מחבר בין 2 קודקודים הוצאנו כל אלכסון פעמים, פעם אחת מכל קודקוד), ולכן יש לחלק את התוצאה בשניים. מספר האלכסונים במצולע הוא, אפוא:
- , כאשר n הוא מספר הצלעות במצולע.
לעיתים ישנם לאלכסונים תכונות נוספות, כמו בריבוע או מעוין, ששם הם גם חוצי זווית של הקודקודים מהם הם יוצאים וגם מאונכים זה לזה.
במרובע ניתן לחשב את השטח באמצעות אורכי האלכסונים והזווית שביניהם על ידי הנוסחה:
במצולע קמור כל האלכסונים נמצאים בתוך המצולע, אך במצולע קעור ישנם אלכסונים גם מחוץ למצולע, כאשר לפחות אלכסון אחד עובר כולו מחוץ למצולע.
אלכסון מוגדר גם בגאומטריה של המרחב, שם הוא ישר המחבר בין שני קודקודים לא סמוכים של פאון.
בשפה שאיננה מתמטית, משמשת המילה "אלכסון" לתיאור דבר נטוי, שאינו אנכי או אופקי (קיר אלכסוני, לדוגמה).
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- הערך "אלכסון", במיקרופדיה תלמודית, באתר ויקישיבה


