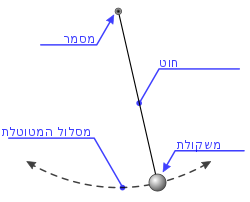
מטוטלת מתמטית (נקראת גם מטוטלת פשוטה ) היא מטוטלת שמורכבת מגוף בעל ממדים קטנים, התלוי על חוט שמסתו ומידת ההתארכות שלו בזמן התנודות ניתנים להזנחה. בנוסף, זווית התנודה של המטוטלת קטנה יחסית. זהו מודל פיזיקלי , שאינו קיים באופן מושלם במציאות, (ולכן המודל מכונה מטוטלת מתמטית), אך בזכות הקירוב ניתן לתאר את תנועת הגוף באופן פשוט. תחת קירוב זה מטוטלת מתמטית היא סוג של אוסצילטור הרמוני , ולכן מהווה מודל לתופעות פיזיקליות רבות.
לאחר הסטת הגוף מנקודת שיווי המשקל ושחרורו, הגוף יבצע תנודות הרמוניות במישור אנכי סביב נקודת שיווי המשקל-לאורך קשת מעגל. זמן המחזור של תנודות מטוטלת מתמטית אינו תלוי במסת המשקולת ובמשרעת (זווית ) התנודות. זוהי תכונה חשובה, שכן היא מאפשרת למדוד מרווחי זמן . בעבר (עד המצאת השעון החשמלי) השתמשו בני האדם בשעון המונע על ידי מטוטלת.
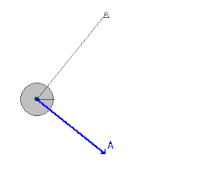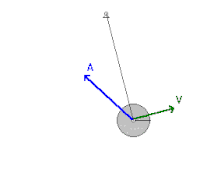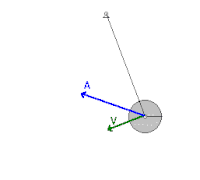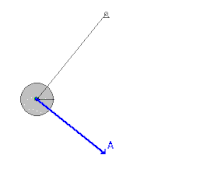
אנימציה של תנועת מטוטלת, המראה את השתנות וקטורי המהירות (V) והתאוצה (A). ניתוח הכוחות על מטוטלת מתמטית ננתח את תנועת המטוטלת, בקירוב בו החוט חסר מסה ואורכו קבוע, מסת המטוטלת נקודתית, וזווית התנודה קטנה. נסמן:
l
{\displaystyle \ l}
m
{\displaystyle \ m}
g
{\displaystyle \ g}
θ
{\displaystyle \ \theta }
ננתח את המומנטים הפועלים על המטוטלת, יחסית לנקודת התלייה. מכיוון שהחוט מחובר לנקודת התלייה, הוא אינו מפעיל מומנט. לכן, המומנט היחיד הפועל על המטוטלת הוא המומנט שמפעיל כוח הכובד , וגודלו
−
m
g
l
sin
θ
{\displaystyle \ -mgl\sin \theta }
העתק ).
מומנט ההתמד של המערכת הוא פשוט
I
=
m
l
2
{\displaystyle I=ml^{2}}
−
m
g
l
sin
θ
=
m
l
2
θ
¨
{\displaystyle \ -mgl\sin \theta =ml^{2}{\ddot {\theta }}}
(ניתן להגיע לנוסחה זו גם על פי משוואת התנועה, מבלי להיכנס למומנט ההתמד .
הדרך שווה לאורך המטוטלת כפול הזווית (ברדיאנים) הנגזרת השנייה של הדרך שווה לתאוצה ששווה ל-g כפול סינוס הזווית
−
g
sin
θ
=
l
θ
¨
{\displaystyle -g\sin \theta =l{\ddot {\theta }}}
באמצעות קירוב זוויות קטנות ,
sin
θ
≈
θ
{\displaystyle \ \sin \theta \approx \theta }
משוואה של אוסצילטור הרמוני :
θ
¨
=
−
g
l
θ
{\displaystyle \ {\ddot {\theta }}=-{\frac {g}{l}}\theta }
הפתרון הכללי של משוואה זו הוא:
θ
=
θ
0
sin
(
ω
t
+
ϕ
)
{\displaystyle \ \theta =\theta _{0}\sin(\omega t+\phi )}
כאשר
ω
=
g
l
{\displaystyle \omega ={\sqrt {\frac {g}{l}}}}
θ
0
,
ϕ
{\displaystyle \ \theta _{0},\phi }
פונקציה מחזורית , בתדירות
f
=
1
2
π
g
l
{\displaystyle f={\frac {1}{2\pi }}{\sqrt {\frac {g}{l}}}}
T
=
2
π
l
g
{\displaystyle \ T=2\pi {\sqrt {\frac {l}{g}}}}
המרחק מנקודת שיווי המשקל הוא
x
=
l
θ
{\displaystyle \ x=l\theta }
x
=
x
0
sin
(
ω
t
+
ϕ
)
{\displaystyle \ x=x_{0}\sin(\omega t+\phi )}
באופן כללי, ניתן לפתור את המשוואה פתרון אנליטי גם ללא הקירוב של זוויות קטנות, בעזרת אינטגרל אליפטי .
במערכת זו, כאשר
H
{\displaystyle H}
המילטוניאן וכאשר
H
=
g
l
{\displaystyle H={\frac {g}{l}}}
ספרטריקס .
הסטייה של זמן המחזור מזמן המחזור המדויק, תוך קירוב זוויות קטנות . ניתן לראות כי עד לזווית מפתח של 30°, מתקבל דיוק טוב מאוד הקטן מ-2%. כאמור, ניתן למצוא את זמן המחזור של מטוטלת פשוטה גם ללא ההנחה של זוויות קטנות, אולם פתרון זה אינו אנליטי (כלומר, לא ניתן להציגו כהרכבה של פונקציות אלמנטריות : פולינומים , אקספוננטים ופונקציות טריגונומטריות ). הפתרון מערב אינטגרל אליפטי , שאותו יש לחשב באופן נומרי .
משימור אנרגיה מתקבל מיידית כי
v
=
2
g
Δ
h
{\displaystyle \ v={\sqrt {2g\Delta h}}}
Δ
h
{\displaystyle \ \Delta h}
v
=
l
d
θ
d
t
{\displaystyle v=l{\frac {d\theta }{dt}}}
d
θ
d
t
=
2
g
Δ
h
l
{\displaystyle {\frac {d\theta }{dt}}={\frac {\sqrt {2g\Delta h}}{l}}}
מצד שני, משיקול גאומטרי ניתן לראות ש
Δ
h
=
l
(
cos
θ
−
cos
θ
0
)
{\displaystyle \ \Delta h=l(\cos \theta -\cos \theta _{0})}
θ
0
{\displaystyle \ \theta _{0}}
המשוואה הדיפרנציאלית
d
θ
d
t
=
2
g
l
(
cos
θ
−
cos
θ
0
)
{\displaystyle {\frac {d\theta }{dt}}={\sqrt {{\frac {2g}{l}}(\cos \theta -\cos \theta _{0})}}}
זוהי משוואה פרידה , וצריך לבצע את האינטגרל
∫
d
t
=
∫
d
θ
2
g
l
(
cos
θ
−
cos
θ
0
)
{\displaystyle \int dt=\int {\frac {d\theta }{\sqrt {{\frac {2g}{l}}(\cos \theta -\cos \theta _{0})}}}}
ניתן לקבל את זמן המחזור על ידי אינטגרציה על רבע מחזור והכפלה ב-4:
T
=
4
∫
θ
0
0
d
θ
2
g
l
(
cos
θ
−
cos
θ
0
)
{\displaystyle T=4\int _{\theta _{0}}^{0}{\frac {d\theta }{\sqrt {{\frac {2g}{l}}(\cos \theta -\cos \theta _{0})}}}}
אינטגרל זה אינו פתיר אנליטית, אך ניתן להביעו באמצעות
F
(
k
,
ϕ
)
{\displaystyle \ F(k,\phi )}
האינטגרל האליפטי של לז'נדר מהסוג הראשון , כך:
T
=
4
l
g
F
(
sin
θ
0
2
,
π
2
)
{\displaystyle T=4{\sqrt {\frac {l}{g}}}F(\sin {\frac {\theta _{0}}{2}},{\frac {\pi }{2}})}
הרחבה - ניתוח האופנים העצמיים למטוטלת בעלת N מתנדים צמודים [ עריכת קוד מקור | עריכה ] מטוטלות מתמטיות צמודות מטוטלת בעלת N מתנדים צמודים, היא בעצם מספר מטוטלות הקשורות זו לזו כאשר החוט של הראשונה יוצא מסוף המטוטלת הקודמת. מספר האופנים העצמיים של מטוטלות מתמטיות צמודות, הוא בדיוק כמספר המתנדים הצמודים שבה. האופנים העצמיים מצביעים על אורך פרקי הזמן שבהם המערכת חוזרת לאותו מבנה מרחבי, ללא חשיבות לזווית ביחס לאנך לרצפה, אלא רק לזוויות בתוך המערכת. עם הוספת מתנד צמוד למטוטלת, האופנים העצמיים שלה מתפלגים באופן הבא: מספר האופנים העצמיים של המערכת גדל והפרש הערכים בין אחד למשנהו קטן. בנוסף לכך, הם הולכים ומתבדרים.
ניתוח מתמטי עבור שני מתנדים צמודים [ עריכת קוד מקור | עריכה ] על מנת לחשב את משוואות התנועה עבור מטוטלת בעלת שני גופים, נשתמש במשוואות אוילר-לגראנז' . לפי משוואות אלו:
T
=
1
2
m
1
v
1
2
+
1
2
m
2
v
2
2
{\displaystyle \ T={\frac {1}{2}}m_{1}v_{1}^{2}+{\frac {1}{2}}m_{2}v_{2}^{2}}
כאשר: T - האנרגיה הקינטית האצורה במערכת.
U, אנרגיית הגובה האצורה במערכת היא:
U
=
−
g
(
R
1
cos
ϕ
(
m
1
+
m
2
)
+
m
2
R
2
cos
ψ
)
{\displaystyle \ U=-g(R_{1}\cos \phi (m_{1}+m_{2})+m_{2}R_{2}\cos \psi )}
פונקציית הלגראנז' L של המערכת היא:
L
=
T
−
U
{\displaystyle \ L=T-U}
ϕ
{\displaystyle \ \phi }
d
d
t
∂
L
∂
ϕ
˙
=
∂
L
∂
ϕ
{\displaystyle \ {\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {\phi }}}}={\frac {\partial L}{\partial \phi }}}
הנגזרות החלקיות בכל אגף מתקבלת המשוואה:
(
I
)
:
m
1
R
1
2
ϕ
¨
+
m
2
R
2
2
ϕ
¨
+
m
2
R
1
R
2
ψ
¨
cos
(
ϕ
−
ψ
)
−
m
2
R
1
R
2
ψ
˙
sin
(
ϕ
−
ψ
)
(
ϕ
˙
−
ψ
˙
)
{\displaystyle \ (I):m_{1}R_{1}^{2}{\ddot {\phi }}+m_{2}R_{2}^{2}{\ddot {\phi }}+m_{2}R_{1}R_{2}{\ddot {\psi }}\cos(\phi -\psi )-m_{2}R_{1}R_{2}{\dot {\psi }}\sin(\phi -\psi )({\dot {\phi }}-{\dot {\psi }})}
=
−
m
2
R
1
R
2
ϕ
˙
ψ
˙
sin
(
ϕ
−
ψ
)
−
g
R
1
sin
ϕ
(
m
1
+
m
2
)
{\displaystyle \ =-m_{2}R_{1}R_{2}{\dot {\phi }}{\dot {\psi }}\sin(\phi -\psi )-gR_{1}\sin \phi (m_{1}+m_{2})}
באותה צורה, מחישוב משוואת אוילר-לגראנז' לפי הזווית
ψ
{\displaystyle \ \psi }
(
I
I
)
:
m
2
R
2
2
ψ
¨
+
m
2
R
1
R
2
ϕ
¨
cos
(
ϕ
−
ψ
)
−
m
2
R
1
R
2
ϕ
˙
sin
(
ϕ
−
ψ
)
(
ϕ
˙
−
ψ
˙
)
{\displaystyle \ (II):m_{2}R_{2}^{2}{\ddot {\psi }}+m_{2}R_{1}R_{2}{\ddot {\phi }}\cos(\phi -\psi )-m_{2}R_{1}R_{2}{\dot {\phi }}\sin(\phi -\psi )({\dot {\phi }}-{\dot {\psi }})}
=
m
2
R
1
R
2
ϕ
˙
ψ
˙
sin
(
ϕ
−
ψ
)
−
g
m
2
R
2
sin
ψ
{\displaystyle \ =m_{2}R_{1}R_{2}{\dot {\phi }}{\dot {\psi }}\sin(\phi -\psi )-gm_{2}R_{2}\sin \psi }
לאחר קירוב לזווית קטנות וארגון המשוואות, מקבלים מ-(I):
(
2
,
1
)
:
R
1
ϕ
¨
+
m
2
m
1
+
m
2
R
2
ψ
¨
=
−
g
ϕ
{\displaystyle \ (2,1):R_{1}{\ddot {\phi }}+{\frac {m_{2}}{m_{1}+m_{2}}}R_{2}{\ddot {\psi }}=-g\phi }
הערה: משמעות הסימונים למשוואות (n,k) הוא: המשוואה ה-k עבור n מתנדים צמודים.
מ-(II) מקבלים:
(
2
,
2
)
:
R
1
ϕ
¨
+
R
2
ψ
¨
=
−
g
ψ
{\displaystyle \ (2,2):R_{1}{\ddot {\phi }}+R_{2}{\ddot {\psi }}=-g\psi }
ניתוח מתמטי עבור שלושה מתנדים צמודים [ עריכת קוד מקור | עריכה ] מחישוב משוואות אוילר לגראנז' בצורה זהה לזו שפורטה לעיל, קירוב לזוויות קטנות, וארגון המשוואות מתקבלות המשוואה הבאות:
(
3
,
1
)
:
R
1
ϕ
¨
+
m
2
+
m
3
m
1
+
m
2
+
m
3
R
2
ψ
¨
+
m
3
m
1
+
m
2
+
m
3
R
3
θ
¨
=
−
g
ϕ
{\displaystyle \ (3,1):R_{1}{\ddot {\phi }}+{\frac {m_{2}+m_{3}}{m_{1}+m_{2}+m_{3}}}R_{2}{\ddot {\psi }}+{\frac {m_{3}}{m_{1}+m_{2}+m_{3}}}R_{3}{\ddot {\theta }}=-g\phi }
(
3
,
2
)
:
R
1
ϕ
¨
+
R
2
ψ
¨
+
m
3
m
2
+
m
3
R
3
θ
¨
=
−
g
ψ
{\displaystyle \ (3,2):R_{1}{\ddot {\phi }}+R_{2}{\ddot {\psi }}+{\frac {m_{3}}{m_{2}+m_{3}}}R_{3}{\ddot {\theta }}=-g\psi }
(
3
,
3
)
:
R
1
ϕ
¨
+
R
2
ψ
¨
+
R
3
θ
¨
=
−
g
θ
{\displaystyle \ (3,3):R_{1}{\ddot {\phi }}+R_{2}{\ddot {\psi }}+R_{3}{\ddot {\theta }}=-g\theta }
בעזרת שש המשוואות שפותחו לעיל, ננסח עתה נוסחה כללית עבור מספר (k) של מתנד במטוטלת בעלת N מתנדים:
(
N
,
k
)
∑
i
=
1
K
R
i
ϕ
¨
i
+
∑
i
=
k
+
1
N
ϕ
¨
i
R
i
∑
j
=
i
N
m
i
∑
j
=
k
N
m
i
=
−
g
ϕ
k
{\displaystyle \ (N,k)\sum _{i=1}^{K}R_{i}{\ddot {\phi }}_{i}+\sum _{i=k+1}^{N}{\ddot {\phi }}_{i}R_{i}{\frac {\sum _{j=i}^{N}m_{i}}{\sum _{j=k}^{N}m_{i}}}=-g\phi _{k}}
כאשר:
ϕ
i
{\displaystyle \ \phi _{i}}
הערה: אם k=N האיבר האחרון אינו מופיע, משום שהסכום מ-N+1 עד N הוא סכום ריק .


 ערך מורחב – מטוטלות מתמטיות צמודות
ערך מורחב – מטוטלות מתמטיות צמודות














































