סימטריה
יש לשכתב ערך זה. הסיבה היא: ערך חלקי ומבולגן.
| ||
| יש לשכתב ערך זה. הסיבה היא: ערך חלקי ומבולגן. | |
ערך ללא מקורות
| ||
| ערך ללא מקורות | |

סִימֶטְרִיָּה (מיוונית: συμμετρεῖν – למדוד ביחד) בשפה היומיומית מתארת תחושה של פרופורציה, הרמוניה ושיווי משקל, או מושג מתמטי מדויק, שמשתמשים בו במסגרת החוקים של מערכות פורמליות, כגון גאומטריה ופיזיקה לתאר בדרך כלל אובייקט שאינו משתנה תחת כמה טרנספורמציות. מכיוון שיש קשר בין שתי המשמעויות, הן נדונות יחד בערך זה. ההפך של סימטריה הוא אסימטריה.
במתמטיקה[עריכת קוד מקור | עריכה]
בגאומטריה[עריכת קוד מקור | עריכה]
הסימטריה הידועה ביותר היא סימטריה גאומטרית. לרוב, עצם גאומטרי נחשב סימטרי אם קיימת איזומטריה המשמרת אותו במקום. לדוגמה, למעגלים וכדורים יש מספר אינסופי של איזומטריות שיעבירו אותן לעצמן, למשל סיבוב סביב מרכזם. יש מספר סוגי סימטריה במישור, כל אחד מתקשר לסוג שונה של איזומטריה:
- סימטריה סיבובית, שבה הצורה נשמרת תחת סיבוב סביב נקודה קבועה. בהרבה מאוד מקרים, אם חוזרים על הסיבוב הנ"ל מספר פעמים, מקבלים את העתקת הזהות. דוגמאות לסימטריות סיבוביות הן הדגל של האי מאן, צלב קרס ומגן דוד, להם סדרי סימטריה מגודלים 6,4,3 בהתאמה.
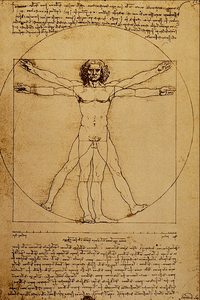
- סימטריה שיקופית, שבה ניתן להעביר ישר שמחלק את הצורה ל-2 חלקים שהן צורות מראה אחת של השנייה. דוגמאות לכך הן מצב הפתיחה של משחק שחמט, האדם הוויטרובי ומשולשים שווי-שוקיים.
- סימטרית הזזה, שבה הגוף נשמר תחת הזזת המישור לכיוון כלשהו. סימטריות כאלו ניתן למצוא במבנים מחזוריים אינסופיים דוגמת סריגי בראבה או ריצוף מחזורי של שטח באריחים זהים.
סימטריית שיקוף[עריכת קוד מקור | עריכה]

 ערך מורחב – שיקוף (מתמטיקה)
ערך מורחב – שיקוף (מתמטיקה)
שיקוף של מישור ביחס לישר הוא העתקה שמעבירה כל נקודה לנקודה הנמצאת במרחק שווה מהישר, כך שהקו המחבר ביניהן מאונך לישר (כלומר הישר הוא אנך אמצעי שלו). את הישר מכנים ציר הסימטריה. הנקודות שעל הישר עצמו נשארות במקומן. זוהי הפעולה המתקבלת כאשר מתבוננים במישור דרך מראה המוצבת על הישר הקבוע. לדוגמה, שיקוף ביחס למראה מאונכת יעביר את האות גימל לאות זין (בכתב יד), וישאיר ללא שינוי את האותיות שין או חית. שיקוף היא העתקה שומרת מרחקים.
השיקוף מתאפיין בכך שהוא העתקה שומרת מרחקים מסדר 2, כלומר, הפעלת השיקוף פעמיים, ביחס לאותו ישר, מחזירה את המרחב לקדמותו. בדומה לזה, הפעלה של שני שיקופים ביחס לישרים מקבילים מהווה הזזה בכיוון המאונך לישרים ובאורך הכפול מהמרחק ביניהם, ואילו הפעלה זו של שני שיקופים ביחס לישרים נחתכים הוא סביב סיבוב של המישור ביחס לנקודת החיתוך שלהם ובזווית כפולה מהזווית ביניהם. כל איזומטריה של המישור ניתנת להגדרה כהרכבה של עד שלושה שיקופים ובהזזה נוכל לקבל צורה.
בניגוד לסיבוב והזזה, השיקוף היא פעולה הופכת אוריינטציה, כלומר את כיוון העצמים. לדוגמה, אם נתון משולש שסדר קודקודיו הם ABC בכיוון השעון, אז הוא יעבור למשולש 'A'B'C שסדר קודקודיו נגד כיוון השעון.
בתורת החבורות[עריכת קוד מקור | עריכה]
 ערך מורחב – חבורת סימטריות
ערך מורחב – חבורת סימטריות
חבורות רבות הן תמורות על איברי קבוצה מסיימת, תחת התנאי שהפעולה משמרת מספר תכונות. דוגמאות לכך הן החבורה הדיהדרלית, חבורת איזומטריות וחבורת ההעתקות פרויקטיביות. עבור מבנה מתמטי, חבורת הסימטריות היא למעשה חבורת האוטומורפיזמים של המבנה.
באמנות החזותית[עריכת קוד מקור | עריכה]
בפילוסופיה[עריכת קוד מקור | עריכה]
בדיאלוג טימאוס משווה אפלטון את חמשת הפאונים האפלטוניים לארבעת היסודות וליקום. בהתאמה זו, היקום מתאים לתריסרון, שהוא הקרוב ביותר בצורתו לכדור, שהוא "המושלמת בין הצורות והדומה ביותר לעצמה". כל הפאונים האפלטוניים סימטריים, אבל הכדור נחשב בעיני אפלטון ליותר סימטרי מהם, משום שיש אינסוף דרכים להעתיק אותו אל עצמו.
סימטריה היא מושג מרכזי בענף הפילוסופי אסתטיקה. אריסטו גרס כי "צורות היופי העיקריות הן סדר, סימטריה ומוגדרות, הבאים לידי ביטוי במיוחד במדעי המתמטיקה" (אריסטו, מטאפיזיקה).
בביולוגיה[עריכת קוד מקור | עריכה]

 ערך מורחב – כיראליות#כיראליות_בביולוגיה
ערך מורחב – כיראליות#כיראליות_בביולוגיה
למולקולות כיראליות, היינו סימטריות, יכול להיות תפקוד שונה לחלוטין במערכות ביולוגיות, לעיתים הגוף יודע לנצל רק צורת מראה אחת של מולקולה, לעומת השנייה.
בכימיה[עריכת קוד מקור | עריכה]
פעולת סימטריה, המשאירה מולקולה ללא שינוי, כלומר, באוריינטציה זהה למקורית, נקראת פעולת זיהוי (המושג אוריינטציה זהה אינו זהה למושג אוריינטציה שקולה). כאשר מסובבים את ציר C2 פעם אחת, אז מתקבלת אוריינטציה שקולה, ורק הסיבוב השני ייתן אוריינטציה זהה. ציר C3 בסיבוב °120 סביב ציר יתן לנו אוריינטציה שקולה למקורית, כך גם סיבוב ב- °240, ורק הסיבוב השלישי סביב ציר המולקולה תוביל לזהות. פעולת הזיהוי מסמנים ב-I. אי פעולה אף היא זהות: אם אין משנים את מצבה של מולקולה, הרי ברור שהוא נשאר כפי שהיה. אפשר לסובב מולקולות במגמת השעון ונגד מגמת השעון. למשל, פעולות C3 במגמת השעון ונגד מגמת השעון נותנות אוריינטציות שקולות, אך לא זהות.
בפיזיקה[עריכת קוד מקור | עריכה]
בפיזיקה המודרנית נעשה שימוש רב בסימטריות. כאשר קיימת סימטריה מסוימת למערכת פיזיקלית ניתן ללמוד מכך רבות על התכונות של אותה המערכת. הדוגמה החשובה ביותר לכך היא משפט נתר לפיו כל סימטריה גוררת חוק שימור בקואורדינאטה הצמודה. לדוגמה, סימטריה של חוקי הפיזיקה בזמן גוררת את חוק שימור האנרגיה.
הסימטריה המרחבית היא כלי מאוד חשוב בקריסטלוגרפיה, בה מטפלים לרוב בגבישים בעלי מבנה מחזורי (חתיכות גדולות של סריגי בראבה או סריג בראבה עם בסיס).
נושא הסימטריות התגלה כחשוב ביותר גם בפיזיקה של חלקיקים אלמנטריים, כאשר יובל נאמן ומארי גל-מאן גילו שאם מסדרים קבוצה מסוימת של חלקיקים לפי התכונות שלהם מקבלים מבנה של חבורה. יש קשר בין הסימטריות של חבורה זו למבנה המרחב-זמן. במסגרת תורת המיתרים נידון גם הנושא של סימטריית-על. יוג'ין ויגנר זכה בפרס נובל על "תרומתו לתאוריה של גרעין האטום והחלקיקים הבסיסיים ובייחוד התגלית והיישום של עקרונות הסימטריה הבסיסיים".
בגאולוגיה[עריכת קוד מקור | עריכה]
הסימטריה בגאולוגיה קיימת בתחום הסטרוקטורלי (מבני) בכל הקשור למבנים כמו אנטיקלינה או סינקלינה. הם יכולים להיות בעלי מבנה סימטרי – שהמדרונות שלהם משני צידי הקמר או הקער הם סימטריים, או אסימטריים.
באדריכלות[עריכת קוד מקור | עריכה]


סימטריה לרוב נתפסת כדוגמה לאסתטיקה וליופי, ולכן בניינים, קומפוזיציות, פסלים וגנים לרוב נעשים בצורה סימטרית. באדריכלות של העת העתיקה וימי הביניים הייתה שאיפה לבנות מבנים סימטריים, כאשר הסימטריה העיקרית היא סימטריית שיקוף ימין-שמאל. יש חוקרים הטוענים שהסימטריה בכנסיות ימי הביניים הייתה רק מקורבת ובכוונה נשתלו בה פגמים קטנים כדי להעביר מסר שרק אלוהים מושלם.
חלופות[עריכת קוד מקור | עריכה]
האמנות המודרנית דווקא אינה דוגלת תמיד בסימטריה. כך, למשל, לה קורבוזיה, מהאדריכלים הנודעים של המאה ה-20, טען כי "הסימטריה היא ההרמוניה של העניים", והעדיף את השימוש ביחס הזהב.
ראו גם[עריכת קוד מקור | עריכה]
לקריאה נוספת[עריכת קוד מקור | עריכה]
- איאן סטיוארט, מרטין גולוביצקי, סימטריה נוראה - האם אלוהים הוא גיאומטריקן?, מאנגלית: עמנואל לוטם, זמורה ביתן, 2001
- מריו ליביו, שפת הסימטריה – המשוואה שלא נמצא לה פתרון, הוצאת אריה ניר, 2006
- מרכוס דו סוטוי, סימטריה, מסע אל מרחבי התבניות של הטבע, מאנגלית: אוריאל גבעון, ספרי עליית הגג, ידיעות ספרים, 2010
- Giora Hon, and Bernard R. Goldstein, 2008. From Summetria to Symmetry: The Making of a Revolutionary Scientific Concept. Archimedes: New Studies in the History and Philosophy of Science and Technology, 20. Dordrecht: Springer
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- הסבר על סימטריה – מתוך מילון המושגים בגאומטריה של משרד החינוך.
- אבשלום אליצור, שמאל דוחה וימין מקרבת: סימטריה ושימור צורה בעולם החיים
- ד"ר מאיר בוזגלו, סדרת הרצאות אודות סימטריה, ערוץ האוניברסיטה העברית ב-יוטיוב
- סימטריה שיקופית וסיבובית, באתר לרגו (LerGO)
 הניו יורק טיימס, מדוע הטבע מעדיף סימטריה? סוף סוף יש תשובה, באתר הארץ, 28 במרץ 2022
הניו יורק טיימס, מדוע הטבע מעדיף סימטריה? סוף סוף יש תשובה, באתר הארץ, 28 במרץ 2022 סימטריה, דף שער בספרייה הלאומית
סימטריה, דף שער בספרייה הלאומית
- J.Rosen, Symmetry at the foundations of science(הקישור אינו פעיל), Computers & Mathematics with Applications, Volume 17, Issues 1–3, 1989, Pages 13-15 (באנגלית)
