ישר
בגאומטריה, יָשָׁר הוא מושג יסודי, המאופיין באמצעות האקסיומות העוסקות בו. לישר יש ממד אחד ויחיד - אורך. בגאומטריה אוקלידית ישר נבנה באמצעות סרגל. בגאומטריה אנליטית ישר במישור הוא אוסף נקודות המקיימות משוואה ליניארית נתונה. בגאומטריה ספירית הישר מיוצג (כלומר מקיים את כל האקסיומות) על ידי מעגל גדול על-פני ספירה והנקודה מיוצגת על ידי זוג נקודות אנטיפודיות.
אקסיומות הישר[עריכת קוד מקור | עריכה]
אקסיומות הגאומטריה העוסקות בישר:
- לכל שתי נקודות שונות זו מזו יש ישר אחד ויחיד ששתי נקודות אלה נמצאות עליו.
- כל ישר מכיל לפחות נקודה אחת.
- מחוץ לכל ישר יש לפחות נקודה אחת.
- אם לישר ולמישור שתי נקודות משותפות שונות זו מזו, הישר נמצא במישור.
- האקסיומה של פאש: אם: הישר x אינו מכיל אף אחת משלוש הנקודות C ,B ,A שאינן על ישר אחד, ו-x מכיל נקודה שבין A ל-B; אז מתקיים אחד מן השניים (ואחד בלבד): או ש-x מכיל נקודה בין A ל-C או ש-x מכיל נקודה בין B ל-C.
- מאקסיומות הגאומטריה ניתן להוכיח כי יש לפחות ישר אחד וכי כל ישר מכיל אינסוף נקודות.
מושגים גאומטריים המתבססים על הישר[עריכת קוד מקור | עריכה]
- קטע הוא חלק של ישר המצוי בין שתי נקודות מסוימות שעליו (בין אם כולל את שתי הנקודות - ואז הוא נקרא קטע סגור, אינו כולל את שתי הנקודות ואז נקרא קטע פתוח או כולל רק אחת מהן - קטע חצי סגור וחצי פתוח). שתי הנקודות נקראות קצות הקטע והקטע המוגדר על ידן מכונה בשם הקטע המחבר את שתי הנקודות.
- קרן היא חלק של ישר שמתחיל בנקודה מסוימת ונמשך עד אינסוף.
או, בהגדרה מדויקת: קרן היא קבוצת נקודות על הישר שאינה קטע ואינה מכילה את כל נקודות הישר ואשר כל קטע המחבר שתי נקודות עליה מוכל בה. נקודה נקראת ראשית הקרן אם כל קטע פתוח על הישר המכיל אותה - מכיל נקודה בקרן ונקודה מחוץ לקרן. קרן המכילה את הראשית שלה נקראת קרן סגורה. קרן שאינה מכילה את הראשית נקראת קרן פתוחה. - קו שבור הוא אוסף של קטעים ישרים עוקבים (כלומר, נקודת ההתחלה של קטע אחד היא נקודת הסוף של אחר).
- מצולע הוא קו שבור סגור (לקטע האחרון והראשון נקודת קצה משותפת) ופשוט (לא חותך את עצמו).
משוואת הישר[עריכת קוד מקור | עריכה]
משוואת ישר במישור[עריכת קוד מקור | עריכה]
משוואת הישר במישור x-y בצורה הכללית ביותר היא
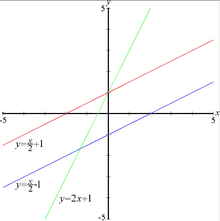
אם נוח להציג את הישר כפונקציה , כלומר:
הגודל הוא השיפוע של הישר, ומתקיים ש- כאשר היא הזווית בין הישר לבין ציר ה-x. הקבוע קובע איפה יחתוך הישר את ציר ה-y ב-x=0.
משוואת הישר העובר דרך נקודה ששיפועו הוא נתונה על ידי
את המשואה אפשר להציג גם כך: , כאשר הוא הווקטור (שלמעשה מהווה הנורמל של הישר) ו- הוא הווקטור .
המשוואה של ישר העובר דרך שתי נקודות נתונות, ו- היא:
- .
אם x0 ≠ x1, ניתן לכתוב משוואה זו בצורה:
או
- .
משוואת ישר במרחב[עריכת קוד מקור | עריכה]
ניתן להציג ישר במרחב בעל ממדים ( ) בהצגה וקטורית בצורה הבאה:
כאשר הוא נקודה על הישר, הוא וקטור הכיוון, ו- הוא סקלר (אשר "רץ" על כל הערכים הממשיים).
במקרה של ישר העובר דרך שתי נקודות במרחב , אפשר להגיע להצגה זאת בדרך הבאה:
קל לראות שעבור t=0 מקבלים את ועבור t=1 מקבלים את .
ניתן להציג ישר במרחב כזה גם כצירוף של משוואות ליניאריות.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- ישר, באתר MathWorld (באנגלית)
- ישר, באתר אנציקלופדיה בריטניקה (באנגלית)






























