מעגל חסום – הבדלי גרסאות
מ הוספת תבנית:MathWorld בקישורים חיצוניים (תג) (דיון) |
מ ←המעגל החסום במשולש: עריכה |
||
| שורה 3: | שורה 3: | ||
== המעגל החסום במשולש == |
== המעגל החסום במשולש == |
||
[[קובץ:Triangle.Incircle.png|שמאל|ממוזער|250px|מעגל חסום במשולש]] |
[[קובץ:Triangle.Incircle.png|שמאל|ממוזער|250px|מעגל חסום במשולש]] |
||
במשולש, מרכז המעגל החסום הוא ה[[נקודה (גאומטריה)|נקודה]] שבה נפגשים שלושת [[חוצה זווית|חוצי הזוויות]] של המשולש. הסיבה לכך היא שחוצה הזווית הוא ה[[מקום גאומטרי|מקום הגאומטרי]] של הנקודות שמרחקיהן משתי הצלעות שווים זה לזה, ומרחקו של מרכז המעגל החסום משלוש הצלעות |
במשולש, מרכז המעגל החסום הוא ה[[נקודה (גאומטריה)|נקודה]] שבה נפגשים שלושת [[חוצה זווית|חוצי הזוויות]] של המשולש. הסיבה לכך היא שחוצה הזווית הוא ה[[מקום גאומטרי|מקום הגאומטרי]] של הנקודות שמרחקיהן משתי הצלעות שווים זה לזה, ומרחקו של מרכז המעגל החסום משלוש הצלעות הוא קבוע. |
||
מכיוון שהמעגל כולו נמצא בתוך המשולש, הרי שבפרט מרכזו של המעגל החסום נמצא תמיד בתוך המשולש (להבדיל ממרכז ה[[מעגל חוסם|מעגל החוסם]] שנמצא בתוך המשולש, על אחת הצלעות או מחוץ למשולש, בהתאם לסוג המשולש). |
מכיוון שהמעגל כולו נמצא בתוך המשולש, הרי שבפרט מרכזו של המעגל החסום נמצא תמיד בתוך המשולש (להבדיל ממרכז ה[[מעגל חוסם|מעגל החוסם]] שנמצא בתוך המשולש, על אחת הצלעות או מחוץ למשולש, בהתאם לסוג המשולש). |
||
נסמן ב- |
נסמן ב-<math>p = \frac{a+b+c}{2}</math> את מחצית [[היקף]] המשולש. רדיוס המעגל החסום הוא <math>\ r = \frac{S}{p}</math>, כאשר S הוא [[שטח]] המשולש, שאותו אפשר לחשב לפי [[נוסחת הרון]] <math>S = \sqrt{p(p-a)(p-b)(p-c)}</math>. |
||
[[משפט אוילר (גאומטריה)|משפט אוילר]], הקרוי של שמו של ה[[מתמטיקאי]] [[לאונרד אוילר]], קובע כי המרחק d בין מרכז המעגל החוסם ומרכז המעגל החסום של [[משולש]] מקיים: <math>d^2 = R\cdot(R - 2r)</math>, כאשר R הוא [[רדיוס]] המעגל החוסם ו- r הוא רדיוס המעגל החסום. מנוסחה זו נובע כי <math>R\ge 2r</math>. |
[[משפט אוילר (גאומטריה)|משפט אוילר]], הקרוי של שמו של ה[[מתמטיקאי]] [[לאונרד אוילר]], קובע כי המרחק d בין מרכז המעגל החוסם ומרכז המעגל החסום של [[משולש]] מקיים: <math>d^2 = R\cdot(R - 2r)</math>, כאשר R הוא [[רדיוס]] המעגל החוסם ו- r הוא רדיוס המעגל החסום. מנוסחה זו נובע כי <math>R\ge 2r</math>. |
||
הקטעים המחברים את קודקודי המשולש עם נקודות ההשקה של הצלעות למעגל החסום, נפגשות בנקודה אחת הקרויה |
הקטעים המחברים את קודקודי המשולש עם נקודות ההשקה של הצלעות למעגל החסום, נפגשות בנקודה אחת הקרויה [[נקודת ז'רגון]] {{אנ|Incircle_and_excircles_of_a_triangle#Gergonne_triangle_and_point}} של המשולש. |
||
==מעגל חסום במצולע משוכלל== |
==מעגל חסום במצולע משוכלל== |
||
גרסה מ־19:36, 14 בספטמבר 2019
בגאומטריה של המישור, מעגל חסום במצולע הוא מעגל המשיק לכל הצלעות של המצולע. בין המצולעים שיש להם מעגל חסום: כל המשולשים וכל המצולעים המשוכללים. מלבן (שאינו ריבוע) הוא דוגמה למצולע שאין לו מעגל חסום.
המעגל החסום במשולש
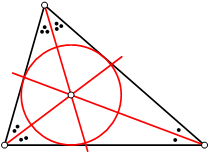
במשולש, מרכז המעגל החסום הוא הנקודה שבה נפגשים שלושת חוצי הזוויות של המשולש. הסיבה לכך היא שחוצה הזווית הוא המקום הגאומטרי של הנקודות שמרחקיהן משתי הצלעות שווים זה לזה, ומרחקו של מרכז המעגל החסום משלוש הצלעות הוא קבוע.
מכיוון שהמעגל כולו נמצא בתוך המשולש, הרי שבפרט מרכזו של המעגל החסום נמצא תמיד בתוך המשולש (להבדיל ממרכז המעגל החוסם שנמצא בתוך המשולש, על אחת הצלעות או מחוץ למשולש, בהתאם לסוג המשולש).
נסמן ב- את מחצית היקף המשולש. רדיוס המעגל החסום הוא , כאשר S הוא שטח המשולש, שאותו אפשר לחשב לפי נוסחת הרון .
משפט אוילר, הקרוי של שמו של המתמטיקאי לאונרד אוילר, קובע כי המרחק d בין מרכז המעגל החוסם ומרכז המעגל החסום של משולש מקיים: , כאשר R הוא רדיוס המעגל החוסם ו- r הוא רדיוס המעגל החסום. מנוסחה זו נובע כי .
הקטעים המחברים את קודקודי המשולש עם נקודות ההשקה של הצלעות למעגל החסום, נפגשות בנקודה אחת הקרויה נקודת ז'רגון (אנ') של המשולש.
מעגל חסום במצולע משוכלל

במצולע משוכלל, מרכז המעגל החסום מתלכד עם מרכז המעגל החוסם.
נסמן:
- n - מספר הצלעות של המצולע המשוכלל
- t - אורך הצלע במצולע המשוכלל
- R - רדיוס המעגל החוסם
- r - רדיוס המעגל החסום.
מתקיים:
חתכי חרוט
משפט פונסלה, שהוא אחד המשפטים החשובים בגאומטריה פרויקטיבית, קובע שאם C,D הם חתכי חרוט ויש מצולע בן n צלעות החסום באחד מהם וחוסם את השני, אז יש אינסוף מצולעים כאלה, וכולם בעלי אותו מספר צלעות.[1]
תחום שבת
המשנה במסכת עירובין עוסקת בקביעת תחום שבת, ובין השאר נאמר בה:
אִם אֵינוֹ מַכִּיר, אוֹ שֶׁאֵינוֹ בָקִי בַהֲלָכָה, וְאָמַר, שְׁבִיתָתִי בִמְקוֹמִי, זָכָה לוֹ מְקוֹמוֹ אַלְפַּיִם אַמָּה לְכָל רוּחַ.
עֲגֻלּוֹת, דִּבְרֵי רַבִּי חֲנִינָא בֶּן אַנְטִיגְנוֹס.
וַחֲכָמִים אוֹמְרִים, מְרֻבָּעוֹת, כְּטַבְלָא מְרֻבַּעַת, כְּדֵי שֶׁיְהֵא נִשְׂכָּר לַזָּוִיוֹת:
לדברי רבי חנינא בן אנטיגנוס תחום שבת של אדם זה הוא מעגל שרדיוסו אלפיים אמה, וחכמים אומרים שתחום שבת הוא ריבוע החוסם מעגל זה. בהתאם לדברי חכמים, בכיוון האלכסון המרחק שנכלל בתוך תחום שבת הוא אלפיים אמה כפול , כלומר 2,828 אמות. בפירושו למשנה מציין פינחס קהתי: "ויש סוברים שיש לו לכל רוח כמידת האלכסון", כלומר שתחום שבת של אדם זה הוא המעגל החוסם של הריבוע, שהוא מעגל שרדיוסו 2,828 אמות.
ראו גם
קישורים חיצוניים
הערות שוליים
- ^ ראו Bull. Amer. Math. Soc. 51(3), 2014, pp. 373--445.









