עקומת ROC
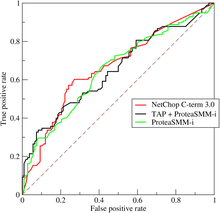
בסטטיסטיקה, עקומה אופיינית למסווג, או עקומת ROC, היא גרף המציג את הביצועים של מסווג דו-ערכי, לאור סף ההחלטה שנקבע לו. העקומה נוצרת על ידי התוויית שיעור החיוביים האמיתיים (TPR) מול שיעור החיוביים הכוזבים (FPR) תחת ספי קבלה שונים. שיעור החיוביים האמיתיים ידוע גם כרגישות או כיסוי בלמידת מכונה. שיעור החיוביים הכוזבים ידוע גם כדלף וניתן לחשב אותו כ־1 פחות הסגוליות. עקומת ROC היא, אם כן, הרגישות כפונקציה של הדלף. באופן כללי, אם התפלגות ההסתברות ידועה הן לפגיעה (Hit, חיובי אמיתי) והן לאזעקת שווא (חיובי כוזב), ניתן לייצר את עקומת ROC על ידי התוויית פונקציית הסתברות הפגיעות (שיעור חיוביים אמיתיים) בציר ה־y לעומת פונקציית ההסתברות לאזעקת שווא (שיעור חיוביים כוזבים) בציר ה־x.
ניתוח ROC מספק כלים לבחירת מבחן (או מסווג) אופטימלי, בטרם מתחשבים בהקשר העלות של כל אחת מסוגי הטעויות או בהתפלגות הפרטים בין הקבוצות. ניתוח ROC קשור באופן ישיר וטבעי לניתוח עלות/תועלת של קבלת החלטות.
עקומת ROC פותחה לראשונה על ידי מהנדסי חשמל ורדאר במהלך מלחמת העולם השנייה, על מנת לשפר את הזיהוי של כלי האויב. לאחר זמן לא רב, הרעיון אומץ בתחום הפסיכולוגיה, כדי להסביר זיהוי של גירויים על ידי החושים. מאז, ניתוח ROC הופעל במגוון תחומים, ביניהם רפואה, רדיולוגיה, ביומטריה ועוד. בעת האחרונה גובר השימוש בניתוח זה בתחום למידת המכונה וכריית המידע.
עקרונות פעולה
[עריכת קוד מקור | עריכה]מבחן (מסווג או בדיקת אבחון) הוא פונקציה שמקשרת בין כל פרט או מקרה לבין קטגוריה או מחלקה מסוימת. תוצאת הסיווג או האבחון היא לרוב בדידה. אם תוצאת המבחן היא רציפה (בעלת ערך ממשי) – אז דרוש לקבוע סף אבחנה בין הקטגוריות השונות (למשל, כדי לבדוק האם אדם חולה ביתר לחץ דם, על פי מדידת לחץ הדם שלו בזמן מסוים, יש לבחור ערך סף שמעליו האדם יוגדר חולה).
במקרה שהאבחנה היא בין שתי קטגוריות בלבד (סיווג דו־ערכי), נהוג לסמן את אחת האפשרויות כ"חיובית" והאחרת – "שלילית". במקרה כזה, קיימות ארבע אפשרויות: אם האבחנה היא חיובית והערך האמיתי גם הוא חיובי, הפרט נקרא "חיובי אמיתי"; אם הערך האמיתי הוא דווקא שלילי, הפרט הוא "חיובי כוזב". מאידך, אם הערך האמיתי הוא שלילי, אם האבחנה גם היא שלילית, הפרט ייקרא "שלילי אמיתי", והפרט ייקרא "שלילי כוזב" אם הערך האמיתי הוא דווקא חיובי. ניתן להציג ערכים אלו בעזרת מטריצת טעות.
 | ||||||||||||||
| תיאור גרפי של מטריצת הטעות: הקו החוצה מפריד בין הפריטים החיוביים (משמאל) לבין הפריטים השליליים (מימין). האליפסה מתארת את המסווג: הפריטים בתוך האליפסה סומנו על ידי המסווג כחיוביים, ומחוץ לה – כשליליים. | ||||||||||||||
| ||||||||||||||
| ||||||||||||||
מתוך מטריצת הטעות, ניתן לחלץ כמה מדדים. עקומות ROC מתחשבת רק בשניים ממדדים אלו: שיעור החיוביים האמיתיים (בקיצור, שח"א), ושיעור החיוביים הכוזבים (שח"כ) – שניהם כפונקציה בפרמטר מסוים של המסווג. השח"א מוגדר כמספר החיוביים הנכונים מתוך כל הנדגמים שהיו באמת החיוביים, והשח"כ מוגדר כמספר החיוביים השגויים מתוך כל הנדגמים שהיו באמת השליליים.
מרחב ROC
[עריכת קוד מקור | עריכה]מרחב ROC מוגדר על ידי שני מספרים אלו – שח"כ FPR בציר האופקי, ושח"א TPR בציר האנכי, ומבטא את העלות (במונחי שח"כ) והתועלת (במונחי שח"א) למבחן מסוים.
במרחב זה, כל מבחן מיוצג כנקודה. המבחן האידיאלי (או: הסיווג המושלם) יופיע במרחב כנקודה בפינה השמאלית העליונה (0,1) של המרחב, כלומר אין פרטים חיוביים כוזבים ואין פרטים שליליים כוזבים (כלומר: כל הפרטים חיוביים נתגלו על ידי המסווג).
ניחוש אקראי לחלוטין ייוצג כנקודה על הקו האלכסוני מהפינה השמאלית התחתונה לנקודה הימנית העליונה (מקווקו אדום, בתמונה). למשל: הטלת מטבע הוגן תתקרב, ככל שהמדגם גדל, למבחן שנמצא בנקודה (0.5,0.5). בדומה, מבחן שנותן תוצאה חיובית לכל הפרטים יגרום ל־100% חיוביים אמיתיים אבל גם ל-100% חיוביים כוזבים, ויסומן כנקודה בפינה הימנית העליונה.
האלכסון, אם כן, מחלק את מרחב ROC לשני חלקים: נקודות מעליו מייצגות סיווג מוצלח (עדיף על בחירה אקראית), ונקודות מתחתיו סיווג רע (גרוע מבחירה אקראית). יצוין שאם מסווג נמצא מתחת לאלכסון אחרי בדיקה במדגם גדול מספיק, ניתן פשוט להפוך את הסיווג שלו משלילי לחיובי ולהפך, כדי לקבל סיווג מוצלח.

דוגמה
[עריכת קוד מקור | עריכה]בדוגמה הבאה מוצגים ארבעה סיווגים שונים ממדגם שבו 100 פרטים חיוביים ו־100 שליליים:
| A | B | C | C′ | ||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
| ||||||||||||||||||||||||||||||||||||
| שח"א = 0.63 | שח"א = 0.77 | שח"א = 0.24 | שח"א = 0.76 | ||||||||||||||||||||||||||||||||||||
| שח"כ = 0.28 | שח"כ = 0.77 | שח"כ = 0.88 | שח"כ = 0.12 | ||||||||||||||||||||||||||||||||||||
| PPV = 0.69 | PPV = 0.50 | PPV = 0.21 | PPV = 0.86 | ||||||||||||||||||||||||||||||||||||
| F1 = 0.66 | F1 = 0.61 | F1 = 0.22 | F1 = 0.81 | ||||||||||||||||||||||||||||||||||||
| נכונות = 0.68 | נכונות = 0.50 | נכונות = 0.18 | נכונות = 0.82 |
ארבעת המסווגים מיוצגים על ידי נקודת במרחב ROC שבתמונה. התמונה מראה בבירור שמסווג A הוא המוצלח ביותר מבין A, B ו־C. תוצאת הסיווג של B נמצאת על קו הניחוש האקראי (האלכסון), וניתן לראות גם שהנכונות של B היא 50%. עם זאת, אם נשקף את נקודה C דרך הנקודה (0.5,0.5), התוצאה המתקבלת, C' היא מוצלחת אפילו יותר מ־A. C' פשוט מחליפה בין הקטגוריות של C (כאשר C מסווגת "שלילי", C' מסווגת חיובי, ולהפך).
PPV= שח"א/(שח"א+שח"כ). PPV מייצג את שיעור החיוביים האמיתיים מתוך כלל החיוביים.
עקומות במרחב ROC
[עריכת קוד מקור | עריכה]
הזזה של סף ההחלטה שקולה לתנועה על עקומת ה-ROC.
סיווגים מבוססים לעיתים רבות על משתנה מקרי רציף. במקרה כזה, ניתן לכתוב את צפיפויות ההסתברות של כל אחת מהקטגוריות כפונקציה של המשתנה המקרי (T). אם נסמן את צפיפות ההסתברות לקטגוריה חיובית ב־ ואת צפיפות ההסתברות לקטגוריה שלילית ב־, נוכל לקבל את הביטויים הבאים לשח"א (TPR) ולשח"כ (FPR) כפונקציה של סף ההחלטה :
כעת, ניתן לשרטט את עקומת ROC של המסווג כפונקציה של הפרמטר .
כדוגמה, נניח שריכוזי החלבונים בדם של חולים ושל בריאים מתפלגים נורמלית סביב ממוצע של 2 גרם לד"ל וגרם אחד לד"ל, בהתאמה. בדיקה רפואית מסוימת עשויה למדוד את ריכוזו של חלבון מסוים בדגימות הדם, ולסווג כדגימה מאדם חולה כל דגימה שבה הריכוז גבוה מערך מוגדר מראש. על ידי הזזת ערך הסף מטה (באיור: הזזת הקו העבה שמאלה), ניתן להגדיל את שיעור החיוביים האמתיים, יחד עם הגדלת שיעור החיוביים הכוזבים, והזזה מעלה (באיור: ימינה) תקטין את שניהם יחד. צורתה של העקומה תיקבע לפי מידת המובחנות בין שני הגירויים (באיור: כמות החפיפה בין שתי ההתפלגויות).
ערכים נגזרים
[עריכת קוד מקור | עריכה]לעיתים, יוצרים מתוך עקומת ROC מדדים נוספים למסווג. דוגמאות נפוצות הן:
- סטטיסטי J של יודן מופיע בגרף כמרחק בין נקודה מסוימת על העקומה, לבין נקודה על האלכסון בעלת אותו שח"כ.
- השטח מתחת לעקומה (המכונה לפעמים A' או איי-פריים).
רקע היסטורי
[עריכת קוד מקור | עריכה]השימוש הראשון בעקומת ROC היה בימי מלחמת העולם השנייה, לשם ניתוח אותות מכ"ם. בעקבות המתקפה על פרל הארבור בשנת 1941, צבא ארצות הברית החל במחקר חדש על מנת להגדיל את יכולת הזיהוי של כלי טיס יפניים על ידי המכ"מים שבידיו.[דרוש מקור]
בשנות ה־50 של המאה ה־20, החלו להימצא עקומות ROC בשימוש הפסיכופיזיקה, על מנת להעריך את יכולת הזיהוי של אותות חלשים על ידי אנשים (ולעיתים גם על ידי בעלי חיים נוספים). ברפואה, ניתוח ROC נמצא בשימוש נרחב לשם הערכות בדיקות אבחון. עקומות ROC גם נמצאות בשימוש נרחב באפידמיולוגיה ומחקר רפואי, ולעיתים קרובות מוזכרות בהקשר של רפואה מבוססת ראיות. ברדיולוגיה, ניתוח ROC הוא טכניקה נפוצה להעריך טכניקות רדיולוגיה חדשות. במדעי החברה, ניתוח ROC, הנקרא בהקשר זה לעיתים קרובות יחס נכונות ROC, הוא טכניקה נפוצה לבחינת הנכונות של מודלים הסתברותיים להפרת הלוואה. עקומות ROC נפוצות גם ברפואת מעבדה כדי להעריך את הדיוק האבחנתי של בדיקה, לבחור את הסף האופטימלי לבדיקה ולהשוות את דיוק אבחון של כמה בדיקות.
יעילותן של עקומות ROC הוכחה גם בהערכת יכולותיהן של שיטות בלמידת מכונה. אחד המיישמים הראשונים של ניתוח ROC בתחום הלמידה החישובית היה קנת ספקמן, שהדגים את חשיבותן של עקומות ROC בהשוואה בין אלגוריתמים שונים לסיווג.[1]
ראו גם
[עריכת קוד מקור | עריכה]לקריאה נוספת
[עריכת קוד מקור | עריכה]- Balakrishnan, Narayanaswamy (1991); Handbook of the Logistic Distribution, Marcel Dekker, Inc., ISBN 978-0-8247-8587-1
- Brown, Christopher D.; and Davis, Herbert T. (2006); Receiver operating characteristic curves and related decision measures: a tutorial, Chemometrics and Intelligent Laboratory Systems, 80:24–38
- Fawcett, Tom (2004); ROC Graphs: Notes and Practical Considerations for Researchers, Pattern Recognition Letters, 27(8):882–891.
- Gonen, Mithat (2007); Analyzing Receiver Operating Characteristic Curves Using SAS, SAS Press, ISBN 978-1-59994-298-8
- Green, William H., (2003) Econometric Analysis, fifth edition, Prentice Hall, ISBN 0-13-066189-9
- Heagerty, Patrick J.; Lumley, Thomas; and Pepe, Margaret S. (2000); Time-dependent ROC Curves for Censored Survival Data and a Diagnostic Marker, Biometrics, 56:337–344
- Hosmer, David W.; and Lemeshow, Stanley (2000); Applied Logistic Regression, 2nd ed., New York, NY: Wiley, ISBN 0-471-35632-8
- Lasko, Thomas A.; Bhagwat, Jui G.; Zou, Kelly H.; and Ohno-Machado, Lucila (2005); The use of receiver operating characteristic curves in biomedical informatics, Journal of Biomedical Informatics, 38(5):404–415
- Stephan, Carsten; Wesseling, Sebastian; Schink, Tania; and Jung, Klaus (2003); Comparison of Eight Computer Programs for Receiver-Operating Characteristic Analysis, Clinical Chemistry, 49:433–439
- Swets, John A.; Dawes, Robyn M.; and Monahan, John (2000); Better Decisions through Science, Scientific American, October, pp. 82–87
- Zou, Kelly H.; O'Malley, A. James; Mauri, Laura (2007); Receiver-operating characteristic analysis for evaluating diagnostic tests and predictive models, Circulation, 115(5):654–7
- Zhou, Xiao-Hua; Obuchowski, Nancy A.; McClish, Donna K. (2002). Statistical Methods in Diagnostic Medicine. New York, NY: Wiley & Sons. ISBN 978-0-471-34772-9.
קישורים חיצוניים
[עריכת קוד מקור | עריכה]הערות שוליים
[עריכת קוד מקור | עריכה]- ^ Spackman, Kent A. (1989). "Signal detection theory: Valuable tools for evaluating inductive learning". Proceedings of the Sixth International Workshop on Machine Learning. San Mateo, CA: Morgan Kaufmann. pp. 160–163.





