לוגריתם

בערך זה נעשה שימוש בסימנים מוסכמים מתחום המתמטיקה. להבהרת הסימנים ראו סימון מתמטי.

לוגריתמים בבסיסים שונים : אדום הוא בבסיס e, צהוב בבסיס 2, כחול בבסיס 1/2. כל שֶ‏נֶ‏ת על גבי הציר היא בגודל יחידה אחת. לוגריתמים בכל הבסיסים עוברים דרך הנקודה (1,0) , שכן כל מספר שאינו 0 ומועלה בחזקת 0 נותן תוצאה 1. בנוסף כולם עוברים דרך (1,"b"), עבור בסיס "b" שכן כל מספר מועלה בחזקת 1 הוא המספר עצמו.

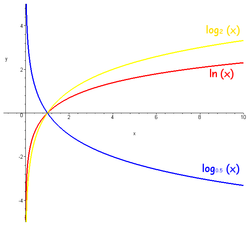
במתמטיקה, לוגריתם (Logarithm) הוא פונקציה הפוכה לפונקציה המעריכית. הפונקציה מסומנת באותיות $\ \log$.

הלוגריתם של $x$ בבסיס נתון $\ b$ (הגדול מאפס ושונה מ-1 ובהתאם x חיובי), הוא החזקה שבה יש להעלות את $\ b$ כדי לקבל את $\ x$.
אם $\ b>0$ ו־$\ x=b^{y}$, נאמר ש־$\ y$ הוא לוגריתם של $\ x$ לפי בסיס $\ b$, ונכתוב זאת: $\ \log _b x=y$.

דוגמה: $\ \log _{10} 100=2$, משום ש- $\ 100=10^2$.

ובמילים: הלוגריתם של $\ 100$ לפי בסיס $\ 10$ הוא $\ 2$, משום ש־$\ 10$ בחזקת $\ 2$ שווה ל־$\ 100$.

בסיס ברירת המחדל:

שימוש בסימון $\ \log$ ללא ציון הבסיס עלול לבלבל מעט, משום שמשמעותו משתנה לפי ההקשר:

• בטקסטים מתמטיים משמעותו $\ \log_{e}$ (הלוגריתם הטבעי, שבסיסו מספר אוילר). נהוג לכתוב פונקציה זו בקיצור $\ \ln$.
• בטקסטים הנדסיים משמעותו $\ \log_{10}$.
• בטקסטים שעוסקים במדעי המחשב משמעותו $\ \log_{2}$, לעתים נכתב בקיצור $\ \mbox{lg}$.

רקע היסטורי

הלוגריתמים הוכנסו לשימוש בתחילת המאה ה-17 על ידי ג'ון נפייר. עד להחלפתם על ידי המחשב והמחשבון, בחצי השני של המאה ה-20, היו הלוגריתמים כלי עזר עיקרי לחישוב, באמצעות לוח לוגריתמים ובאמצעות סרגל חישוב. הרעיון הבסיסי מאחורי שני עזרי חישוב אלה הוא הכלל לפיו לוגריתם של מכפלה שווה לסכום הלוגריתמים של כל אחד מאיברי המכפלה. כלל זה מאפשר להחליף פעולת כפל, שהיא פעולה מורכבת יחסית, בפעולת החיבור הפשוטה יותר. בכלים אלה נעשה שימוש בלוגריתמים לפי בסיס $\ 10$.

חוקי הלוגריתמים

החוקים המפורטים להלן נכונים לכל $\ a, b, c$ ממשיים חיוביים, ובתנאי שבסיס הלוגריתמים שונה מ־1.

ערכים מיוחדים	$\ \log _a (1)=0$ $\ \log _a (a)=1$
כפל, חילוק והעלאה בחזקה חוקים אלו יכולים להקל על חישובי כפל, חילוק, חזקה ושורש, באמצעות לוח לוגריתמים או סרגל חישוב.	$\ \log _c (a\cdot b) = \log _c (a) + \log _c (b)$ $\ \log _c \left(\frac{a}{b}\right) = \log _c (a) - \log _c (b)$ $\ {\log_a b}\cdot{\log_c d}={\log_c b}\cdot{\log_a d}$ לכל $\ r$ ממשי: $\ \log _c (a^r) = r\cdot \log _c (a)$
הלוגריתם והפונקציה המעריכית חוקים אלו שימושיים לפתרון משוואות בהן הנעלם הוא מעריך של חזקה.	$\ x^{\log_a b}=b^{\log_a x}$ $\ a^{\log_a b}=b$ לכל $\ r$ ממשי: $\ \log_a a^r=r$
שינוי בסיס הלוגריתם חוק זה שימושי להמרת לוגריתמים במחשבונים. לרוב המחשבונים יש לחצנים לחישוב לוגריתם טבעי (ln) ולוגריתם בבסיס 10 ($\ \log_{10}$), אבל לא לבסיס 2 ($\ \log_{2}$). כדי לחשב את $\ \log_{2} 100$, מחשבים $\ \frac{\log_{10} 100}{\log_{10} 2}$ או $\ \frac{\ln{100}}{\ln{2}}$, שנותן תוצאה זהה).	$\ \log_a b=\frac{\log_c b}{\log_c a}$ $\ \log_a b=\frac{1}{\log_b a}$
גבולות	כאשר a > 1: $\ \lim_{x\to0} \log_a (x) = -\infty$ כאשר a < 1: $\ \lim_{x\to0} \log_a (x) = \infty$ כאשר a > 1: $\ \lim_{x\to\infty} \log_a (x) = \infty$ כאשר a < 1: $\ \lim_{x\to\infty} \log_a (x) = -\infty$ $\ \lim_{x\to0} \log_a (x) \cdot x^b = 0$ $\ \lim_{x\to\infty} \log_a (x) / x^b = 0$
נגזרת	$\ {d \over dx} \log_a (x) = {1 \over x \ln(a)} = {1 \over x} \cdot log_a e$
אינטגרל	$\ \int \log_a (x)\, dx = x \log_a (x) - \frac{x}{\ln(a)} + C$

ראו גם

• סקאלה לוגריתמית
• לוגריתם חוזר
• נגזרות של פונקציות לוגריתמיות
• פונקציה מעריכית