בקבוק קליין

במתמטיקה, בקבוק קליין הוא משטח קומפקטי דו-ממדי, שאינו ניתן לשיכון במרחב האוקלידי התלת-ממדי, אלא רק במרחב בעל ארבעה ממדים או יותר.
את המשטח חקר לראשונה המתמטיקאי הגרמני פליקס קליין, שבנה אותו (מתמטית) לראשונה ב-1882, על ידי חיבור של שתי טבעות מביוס לאורך שפתן. שני המבנים זכו להתעניינות רבה מצידם של אמנים ויוצרים, ואפילו של פסיכואנליטיקאים. קליין קרא למשטח Kleinsche Fläche, כלומר "משטח קליין", אך הובן בטעות כ-Kleinsche Flasche, כלומר "בקבוק קליין", וטעות זו הפכה לשמו המקובל של המשטח.[1]
בקבוק קליין הוא המשטח היחיד מגנוס 2 שלא ניתן לכוון אותו.
בניה של בקבוק קליין[עריכת קוד מקור | עריכה]
כדי לבנות בקבוק קליין, לוקחים בקבוק יין פתוח (וריק), ויוצרים חור עגול בקרקעית הבקבוק. כעת מושכים את צוואר הבקבוק ומכופפים אותו כלפי מטה, כלפי החור. לו היינו מחברים את צוואר הבקבוק לחור מלמטה, היינו מקבלים צינור סגור, הקרוי טורוס. אלא שמטרתנו שונה - נחבר את הצוואר אל החור מלמעלה - משימה שלשמה נאלץ (בעולמנו התלת-ממדי) לחצות עם צוואר הבקבוק את גוף הבקבוק עצמו. לו היינו פועלים בעולם ארבע-ממדי, לא היה הצוואר צריך לחצות את הגוף, וכך היה מתקבל דגם אמיתי של בקבוק קליין. הנפח של בקבוק קליין הוא אפס: אין לו פנים וחוץ.
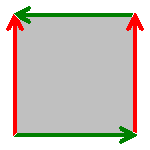
כדי לחסוך את הצורך לעבוד בעולם ארבע-ממדי (ואפילו תלת-ממדי), מתמטיקאים מעדיפים לחקור עצמים טופולוגיים על ידי הדבקה (במחשבה) של צלעות מצולעים (ראו טופולוגיה אלגברית). הרעיון בהדבקה כזו הוא שהמצולע משמש מפה של העצם שאותו חוקרים, וכך אפשר לדמיין שער המוביל מצלע אחת על המפה לצלע אחרת. הדוגמה הפשוטה ביותר היא הדבקה של שתי צלעות נגדיות בריבוע, באותו כיוון. כך מתקבל גליל. אם נדביק גם את שתי הצלעות הנגדיות האחרות זו לזו, באותו כיוון, יהא זה כאילו אנחנו מחברים את קצות הגליל זה לזה (באותו כיוון), וכך יתקבל טורוס. לעומת זאת, אם נדביק את שני המעגלים שבקצות הגליל בכיוונים הפוכים, יתקבל בקבוק קליין.
טבעת מביוס מתקבלת מהדבקה של שתי צלעות בריבוע, בכיוונים הפוכים. מכאן אפשר להסיק שאם מדביקים שתי טבעות מביוס זו לזו מתקבל בקבוק קליין. למעשה, גם אם מדביקים את שפתה של טבעת אחת לעצמה (כפי שאפשר להדביק שפה אחת של גליל לעצמה, ולקבל מעין שקית חלב פתוחה בקצה האחד), מתקבל בקבוק קליין. אפשר להפוך את הסדר, ולומר זאת כך: בקבוק קליין אפשר לחתוך לשתי טבעות מביוס; וגם, באופן שונה, לטבעת אחת.
דרך אחרת להבין משטחים טופולוגיים היא לחורר אותם. אם מחוררים חור קטן בכדור ומותחים את שפת החור, מתקבל (בסופו של דבר) עיגול פתוח. אם חוזרים על אותו מעלל בבקבוק קליין, מתקבלת צורה המורכבת מטבעת רגילה וטבעת מביוס, שהודבקו זו לזו בריבוע משותף.
בקבוק קליין כמשטח[עריכת קוד מקור | עריכה]
הטופולוגיה היא ענף של הגאומטריה, שבו מנסים מתמטיקאים ללמוד מבנים גאומטריים על ידי צמצום נקודת ההסתכלות לאזורים קטנים ("סביבות"). אחד המבנים החשובים בטופולוגיה הוא המשטח - אם מתבוננים בסביבה הסמוכה לכל נקודה על משטח, התמונה דומה לזו שרואים מנקודה במישור (בשפה מתמטית אומרים ש"משטח" הוא מרחב טופולוגי, שהוא הומיאומורפי מקומית לכדור היחידה הפתוח של , כלומר: לדיסק ). מישור הוא דוגמה אחת; פני כדור הם דוגמה אחרת. הכדור שונה מן המישור בכך שיש לו פנים וחוץ, אבל זוהי תכונה שלא ניתן לזהותה כאשר מגבילים את הראות למרחקים קצרים (אכן, בעבר התקשו יושבי כדור הארץ לזהות שהם חיים על פני כדור ולא על מישור).
דוגמה נוספת למשטח הוא עיגול פתוח, כלומר, עיגול, ללא המעגל המקיף אותו. כל נקודה שעל-פני העיגול רחוקה במידת-מה מן הקצה, ולכן היא נראית (בקנה מידה קטן מספיק) כנקודה שעל מישור. לעומת זאת, אם נקיף את העיגול במעגל, התוצאה איננה נחשבת עוד למשטח - משום שמנקודה שעל המעגל נראית תמונה אחרת שונה: מישור מצד אחד, ריקנות מצד שני. במונחים טופולוגיים, המעגל הוא השפה של העיגול. לכדור ולטורוס אין שפה, והם נקראים 'משטחים סגורים'. משטחים שיש להם שפה, כמו העיגול הפתוח, אינם כאלה. אם כך, טבעת מביוס איננה משטח סגור - יש לה שפה, שגם היא (מבחינה טופולוגית) מעגל.
כיווניות של משטחים סגורים[עריכת קוד מקור | עריכה]
מבחינים בין שני סוגים של משטחים המשוקעים במרחב תלת-ממדי: כאלה שיש להם שני צדדים, וכאלה שיש להם רק צד אחד. את הראשונים, כמו פני הכדור או העיגול הפתוח, אפשר לצבוע בשני צבעים; את האחרונים, כמו טבעת מביוס, אי אפשר. משתמשים גם במונח 'כיוון' ("אוריינטציה"): משטחים בעלי שני צדדים הם 'ניתנים לכיוון' ("אוריינטביליים"), בעוד שבעלי צד אחד אינם ניתנים לכיוון. אפשר להבין זאת כך: אם נציב את האות d על משטח שניתן לכיוון ונסיע אותה אנה ואנה, נוכל להחזיר אותה לאותו מקום כך שתראה כמו האות p, אבל לעולם לא נוכל להפוך אותה לאות b. לעומת זאת, על פני משטח שאינו ניתן לכיוון ההבחנה בין ימין ושמאל אינה קיימת, ולכן אפשר יהיה לשקף את הסימן על ידי הסעתו במסלול מתאים.
בקבוק קליין הוא משטח סגור, שכאשר הוא משוקע במרחב התלת-ממדי הוא אינו ניתן לכיוון. (למשטח המשוכן במרחב הארבעה ממדי אין "צדדים", כמו שלעקומה במרחב התלת־ממדי אין צדדים).
הטבעה במרחב התלת-ממדי[עריכת קוד מקור | עריכה]
הטבעה (immersion) היא העתקה הפיכה מקומית של מרחב טופולוגי אחד לשני. אמנם אי-אפשר לשכן את בקבוק קליין במרחב התלת-ממדי, אפשר להטביע אותו שם. דרך אחת לעשות כן מופיעה בציור למעלה; ישנה דרך אחרת, הקרויה "הטבעה בצורת 8", ושתיהן אינן הומוטופיות זו לזו. הטבעה שומרת על האפשרות לכוון משטח, ולכן להטבעה של בקבוק קליין מוכרח להיות צד אחד בלבד; מכאן נובע שכל הטבעה כזו מוכרחה לחתוך את עצמה, ולכן היא איננה מהווה שיכון.
מאפיין אוילר[עריכת קוד מקור | עריכה]
משטחים סגורים אפשר למיין (עד כדי הומיאומורפיזם) לפי הכיווניות ומאפיין אוילר. בקבוק קליין מוגדר כמשטח הסגור (היחיד) שאינו ניתן לכיוון, ומאפיין אוילר שלו שווה לאפס.
את המאפיין של בקבוק קליין אפשר לחשב מתוך העובדה שאפשר לשכן בו את גרף פרנקלין, שהוא גרף בן 12 קודקודים ו-18 צלעות, המחלק את המשטח ל-6 רכיבים. רכיבים אלה מהווים מפה, שאותה לא ניתן לצבוע בפחות משישה צבעים; לכן בקבוק קליין מקיים את "משפט ששת הצבעים", בדומה למשפט ארבעת הצבעים שמקיים הכדור.
החבורה היסודית[עריכת קוד מקור | עריכה]
את בקבוק קליין אפשר לבנות על ידי הדבקה של שתי טבעת מביוס לאורך שפה משותפת, שהיא מעגל. לפי משפט ואן קמפן, החבורה היסודית של המשטח המתקבל היא מכפלת היתוך של שני עותקים של החבורה הציקלית האינסופית, ביחס לתת-החבורות מאינדקס 2, כלומר . זוהי הרחבה מרכזית של החבורה הדיהדרלית האינסופית בחבורה הציקלית האינסופית.
בקבוק קליין בפסיכואנליזה[עריכת קוד מקור | עריכה]
בהרצאה מפורסמת[2] שנשא הפילוסוף והפסיכואנליטיקאי ז'אק לאקאן ב-1966 הוא הסביר שהמגוון של משטחים טופולוגיים שמהם ניתן לחתוך טבעות מביוס, ובכללם בקבוק קליין, הוא "חשוב מאוד, מכיוון שהוא מסביר דברים רבים על המבנה של מחלות נפש". כך למשל "החיתוך בטורוס מקביל לסובייקט הנוירוטי". יצוין שממשטח מכוון כמו הטורוס לא ניתן לחתוך משטח שאינו מכוון, כמו טבעת מביוס.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- בקבוק קליין, באתר MathWorld (באנגלית)
- בקבוק קליין, באתר אנציקלופדיה בריטניקה (באנגלית)
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ סיימון סינג, הסודות המתמטיים של הסימפסונים, תרגם חיים שמואלי, הוצאת ספרי עליית הגג, 2018, עמ' 235
- ^ Jacques Lacan, Of Structure as the Inmixing of an Otherness Prerequisite to Any Subject Whatever