חשבון מודולרי
חשבון מוֹדוּלַרי (הידוע גם כחשבון קונגרואנציות) הוא שיטה מתמטית, בה מחליפים מספרים בשארית החלוקה במספר קבוע. לדוגמה, בחשבון מודולו 7 מתקיים השוויון , מכיוון ש: , ושארית החילוק של 11 ב-7 היא 4.
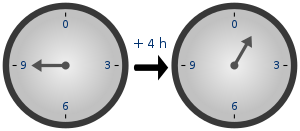
הדוגמה הידועה ביותר לחשבון מודולרי היא החשבון על-פני השעון, שהוא חשבון מודולרי מודולו 24. כאשר השעה כעת היא 20:00, ואנו רוצים לדעת מה תהיה השעה 9 שעות מאוחר יותר, הפעולה שאנו עושים היא .
הגדרה פורמלית[עריכת קוד מקור | עריכה]
יהי n מספר טבעי. המספרים a,b שקולים מודולו n אם n מחלק את ההפרש a-b. המספרים a,b שקולים אם ורק אם הם נותנים אותה שארית בחלוקה ב-n. במקרה זה מסמנים . (אומרים גם ש-a,b קונגרואנטיים מודולו n).
החשבון המודולרי מודולו מתבצע באופן פורמלי על אוסף מחלקות שקילות של המספרים השלמים, כאשר יחס השקילות הוא היחס שהוגדר בפסקה הקודמת. אפשר לבחור במספרים השלמים מ- ועד כנציגים סטנדרטיים של המחלקות, ואז התוצאה של חישוב מודולרי תהיה מוגבלת לקבוצת השאריות האפשריות המתקבלות מחילוק מספר כלשהו ב.
תכונות השקילות המודולרית[עריכת קוד מקור | עריכה]
יחס השקילות המודולרית הוא אכן יחס שקילות, כלומר הוא
בנוסף לזה, פעולות החיבור והכפל בין מחלקות השקילות מוגדרות היטב: אם וכן , אז וכן . לכן קבוצת המספרים השלמים מודולו מהווה חוג קומוטטיבי, עם הכפל והחיבור הטבעיים, שאותו מסמנים ב- או ב- (הסימון האחרון רומז לכך שזהו חוג מנה של חוג המספרים השלמים ביחס לאידיאל של המספרים המתחלקים ב-n). החוג הזה הוא תחום שלמות אם ורק אם מספר ראשוני (ואז הוא שדה).
הופכי ביחס לכפל[עריכת קוד מקור | עריכה]
איבר הוא הפיך אם קיים כך ש- . במקרה זה, b הוא ההופכי כפלי של a. את ההופכי שלו מסמנים כנהוג ב- .
מציאת הופכי כפלי מודולרי, כלומר פתרון המשוואה , נעשית באמצעות אלגוריתם אוקלידס המורחב, המספק ערכים x,y המקיימים , משום שאז . לדוגמה: ההופכי כפלי של הוא כיוון ש- לכן .
חילוק[עריכת קוד מקור | עריכה]
 ערך מורחב – חילוק מודולרי
ערך מורחב – חילוק מודולרי
כפל של , בהופכי כפלי של שלם כלשהו שקול לחילוק ב-, כלומר שקול ל- (מודולו ).
מכיוון שלא כל מספר הפיך מודולו n, לא תמיד אפשר לחלק שוויונות מודולריים. למעשה, אם , אז מובטח רק ש- .
משפט אוילר[עריכת קוד מקור | עריכה]
שני מספרים שלמים נקראים זרים אם המחלק המשותף המרבי שלהם הוא 1. פונקציית אוילר המסומנת מייצגת את מספר השלמים בטווח הזרים ל-. כלומר שהמחלק המשותף המרבי שלהם עם הוא . אם ראשוני אזי כל המספרים עד זרים ל-, כיוון שמספר ראשוני אינו מתחלק באף אחד מהמספרים הנמוכים ממנו מעצם ההגדרה. משפט אוילר קובע שעבור כל שלם שזר ל- מתקיים . כאשר מספר ראשוני מתקבל כמקרה פרטי המשפט הקטן של פרמה: , לכל שלא מתחלק ב-.
חבורות מודולריות[עריכת קוד מקור | עריכה]
פעולת החיבור בחשבון מודולרי היא, בדומה לחיבור הרגיל, קומוטטיבית ואסוציאטיבית, וכן יש בה איבר יחידה (0), ולכל מספר יש איבר נגדי. לפיכך חיבור בחשבון מודולרי יוצר חבורה קומוטטיבית שהיא החבורה הציקלית מסדר n.
גם פעולת הכפל בחשבון מודולרי היא קומוטטיבית ואסוציאטיבית, ואיבר היחידה בה הוא 1, אך לא לכל איבר יש איבר הופכי (כלומר, כזה שמכפלתם של שני האיברים תהיה איבר היחידה 1). לכן אוסף השאריות מודולו n הוא מונואיד ולא חבורה. במונואיד הזה יש מחלקי אפס, כגון . לאבר שהוא מחלק אפס לא יכול להיות הפכי כפלי; ובמונואיד של השאריות מודולו n זו המניעה היחידה לקיומו של הפכי. מספר הוא הפיך מודולו n אם הוא זר ל-n, ומחלק אפס אחרת. אוסף השאריות השונות מאפס הוא חבורה אם ורק אם n ראשוני. באופן כללי יותר, אוסף השאריות ההפיכות נקרא חבורת אוילר של n.
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- גדי אלכסנדרוביץ', אז מה זה בעצם חשבון מודולרי?, באתר "לא מדויק"
- חשבון מודולרי, באתר MathWorld (באנגלית)
- חשבון מודולרי, באתר אנציקלופדיה בריטניקה (באנגלית)


































![{\displaystyle \ [1,n-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c69bc4d24d86e73399d6e6378830cc93d950a5b)






