משתמש:Dtomarov/פונקצית מריחת כתם

פונקציית מריחת כתם (באנגלית: Point Spread Function, או בקיצור PSF) מתארת את האופן בו מערכת המבצעת דימות מורחת את דמותו של מקור אור נקודתי. מערכות דימות מעשיות אינן מושלמות, משום כך הן גורמות לעיוות אור העובר דרכן. באופן תאורטי, מערכות דימות מושלמות אינן יוצרות עיוותים כלל, ובפרט נקודת אור תשמר את צורתה במעבר דרך מערכת כזו. מאחר ובמערכות ליניאריות מתקיימת תכונת הסופרפוזיציה, ניתן לקבוע את אופן העיוות של המערכת על ידי בדיקת השפעתה על נקודת אור בודדת.
פונקציית מריחת הכתם היא למעשה תגובת ההלם של מערכת דימות. ידיעת פונקציית מריחת הכתם היא בעלת חשיבות רבה, כיוון שהיא מאפיינת באופן מלא את המערכת ומאפשרת לחשב כל דמות שתיווצר במוצא המערכת כתוצאה מעצם מסויים בכניסתה[1].
פונקציית מריחת הכתם מהווה מדד לטיב המערכת, והיא מופיעה בתחומים רבים כגון: אופטיקת פוריה, הדמיות אסטרונומיות, הדמיות רפואיות, מיקרוסקופיה אלקטרונית וכן בשיטות דימות שונות כדוגמת מיקרוסקופיה תלת-מימדית (לדוגמה סריקה באמצעות מיקרוסקופיה קונפוקלית) ומיקרוסקופיה פלואורוסנטית.
הגדרה כללית יותר לפונקצית מריחת כתם היא תגובת ההלם של המערכת דימות, וניתן לחשוב עליה כעל גרסתה המרחבית של פונקציית תמסורת אופטית.
מבוא
[עריכת קוד מקור | עריכה]
בערכת דימות ליניארית ולא קוהרנטיות מתקיימת תכונת הליניאריות. כלומר כאשר שני עצמים עוברים דימות, הדמות שתיווצר תהיה שווה לסכומן של הדמויות שנוצרו מכל עצם בנפרד:
בהסתמך על ביטוי זה, ניתן לחשב את השדה של הדמות באופן הבא: תחילה מבטאים את השדה של העצם כסכום דו-ממדי של פונקציות הלם ממושקלות, ולאחר מכן מחשבים וסוכמים את הדמויות הנוצרות מכל פונקציית הלם ממושקלת. זהו למעשה עקרון הסופרפוזיציה.

דמות המתאימה לפונקציית הלם ממושקלת יחידה כפי שתוארה קודם, למעשה מתארת את מידת המריחה שמבצעת המערכת לעצם נקודתי, או באופן שקול את השפעת פונקציית מריחת הכתם על עצם נקודתי. במערכות ללא תלות מרחבית, פונקציית מריחת הכתם שווה בכל מקום על מישור המוצא. כאשר העצם מתואר כאוסף של עצמים נקודתיים בעלי עוצמה משתנה, הדמות ניתנת לחישוב על ידי סכימה של פונקציות פיזור הנקודה של העצמים הנקודתיים. ייצוג זה מתואר על ידי פעולת הקונבולוציה.
כיוון שפונקציית מריחת הכתם מאופיינת על ידי מערכת הדימות, ניתן לדעת כיצד תראה הדמות מתוך ידעת המאפיינים האופטיים של המערכת. בתחום עיבוד תמונה של מיקרוסקופים וכן באסטרונומיה, ידיעת פונקציית פיזור הנקודה מאפשרת לשחזר תמונה של העצם המקורי על ידי ביצוע דה קונבולוציה. ביצוע דה קונבולוציה על פונקציית מריחת הכתם ועל הדמות מסלקת רעש ובכך משפרת את היכולת להבחין בפרטים עדינים.
תאוריה ועקרון פעולה
[עריכת קוד מקור | עריכה]במקרה בו פונקציית מריחת הכתם אינה תלויה במיקום על מישור העצם, הפונקציה תקרא "בלתי תלויה בהזזה" (באנגלית: Shift Invariant). בהיעדר עיוותים במערכת (לדוגמה כתוצאה מאברציות), הקואורדינטות של מישור הדמות יהיו תלויות בקואורדינטות של מישור העצם באופן ליניארי על ידי יחס ההגדלה M כדלקמן:
במידה ומערכת הדימות מייצרת דמות הפוכה, ניתן להתיחס לצירים של מישור הדמות כהפוכים בכיוונם לצירים של מישור העצם. מתוך שימוש בהנחות כי פונקציית מריחת הכתם אינה תלויה במיקום כן שאין עיוותים במערכת, נוכל לחשב את אינטגרל הקונבולוציה במישור המוצא. הביטוי מתמטי לאינטגרל זה, שתוצאתו תניב את השדה המתקבל במישור העצם באופן הבא:
כפי שכבר ראינו בפרק המבוא, ניתן לפרש את הביטוי שהתקבל כסכום של פונקציות הלם ממושקלות. בנוסף, זוהי גם תוצאה של שימוש בתכונת הדגימה של פונקציית ההלם הדו-מימדית. הצגה של העצם בצורה זו מאפשר לנו לחשב את שדה הדמות כסופרפוזיציה של דמויות, שכל אחת מהן נובעות מפונקציות הלם נפרדת. במילים אחרות, נוכל לרשום את שדה הדמות כסופרפוזיציה של פונקציות פיזור נקודה ממושקלות במישור הדמות, על ידי אותה פונקציית משקל, שהשתמשנו בה במישור העצם כדי להביע את העצם. הביטוי המתמטי שמתקבל עבור הדמות הוא:
נשים לב כי , היא הדמות של .

פונקציית ההלם הדו מימדית היא פונקציה בצורת "עמוד" עם צלעות בסיס באורך , כאשר . ניתן לתאר את העצם כמרוצף בריבועים זעירים עם בסיס בגודל , ולכל ריבוע פונקציית "עמוד" משלו. אם גובה פונקציית העמוד הוא , ומתקיים כי , ישאף לאינסוף כך שנפח פונקציית העמוד ישאר 1. התוצאה האחרונה מעניקה לפונקציית ההלם הדו מימדית את תכונת הדגימה בה השתמשנו מוקדם יותר. על פי תכונת הדגימה, כאשר נבצע אינטגרציה על מכפלה בין כל פונקציה רציפה לפונקציית ההלם , התוצאה תהיה ערכה של הפונקציה בנקודה .

מגבלותיה של פונקציית ההלם
[עריכת קוד מקור | עריכה]הרעיון של מקור אור נקודתי חיוני בכל הקשור לפונקציית מריחת הכתם. מקור אור שכזה אינו פיזיקלי, ועל כן אינו קיים בטבע. עם זאת, התאור המתמטי של מקור נקודתי עוזר להציג ולהסביר כיצד פועלות מערכות דימות אופטיות. עצם דו מימדי המתואר כמקור אור נקודתי ייצר גל כדורי מושלם בעל אמפליטודה (בעברית: משרעת) אחידה. לגל זה יהיו חזיתות גל כדוריות שוות פאזה ובעלות עוצמה אחידה (עקרון הויגנס-פרנל). נשים לב כי לא רק שמקור אור נקודתי יוצר רצף אחיד של גלים מישוריים מתקדמים, אלא בנוסף גם יוצר רצף אחיד של גלים דועכים בצורה מעריכית. גלים דועכים אלו הם שמאפשרים רזולוציה הקטנה מאורך גל יחיד (ראה אופטיקת פוריה). התמרת פוריה של פונקציית ההלם הדו-מימדית מקיימת:
מפתחים סופיים
[עריכת קוד מקור | עריכה]העדשה הריבועית מעכבת חלק מחזית הגל הכדורי, ובכך ממקדת אותו לנקודה מטושטשת במישור הדמות. במקרה של עדשה בודדת, מקור אור נקודתי במישור העצם הנמצא על הציר הפראקסיאלי, יוצר במישור הדמות פונקציית מריחת כתם בצורת דיסקת איירי. ניתן להראות (ראה אופטיקת פוריה, עקרון הויגנס-פרנל, עקיפת פראונהופר) שהשדה הנוצר מעצם מישורי (או באופן שקול, שדה המתכנס לדמות מישורית) קשור לפילוג השדה של מקור (דמות) על ידי התמרת פוריה. כמו כן, פונקציה אחידה בעלת תמך מעגלי במישור התדר, תתאים לפונקציית איירי במרחב (ולהיפך), כאשר היא פונקציית בסל מסדר ראשון. כלומר הארה אחידה של מפתח עגול שמעביר גל כדורי אחיד ומתכנס, תייצר דמות בצורת פונקציית איירי במישור המוקד.

קיימת חשיבות לארגומנט של פונקציית איירי, כיוון שהוא זה שקובע את מימדי הפונקציה במישור הדמות. אם היא הזווית המקסימלית שהגלים המתכנסים יוצרים עם ציר העדשה, r הוא המרחק הרדיאלי במישור הדמות, ומספר הגל הוא כאשר הוא אורך הגל, אז הארגומנט של פונקציית איירי יהיה: . אם היא זווית קטנה (רק חלק מהגל הכדורי המתכנס יוצר את ההדמות), אז המרחק הרדיאלי יקבל ערך גדול מאוד לפני שנבחין בשינוי כלשהו בארגומנט מהמרכז. ניתן לומר כי אם קטנה, אז דיסקת איירי תהיה רחבה (זהו ניסוח שקול לעקרון אי הוודאות של הייזנברג: תחום צר במישור אחד יוביל לתחום רחב במישור השני, והקשר ביניהם יהיה דרך המכפלת רוחב סרט-מרחב(Space-Bandwidth Product)). לאור זאת, הגדלה משמעותית של המערכת, אשר לרוב תהיה בעלת ערכי קטנים (לפי תנאי הסינוס של Abbe), עשויה להכיל טשטוש רב יותר בגלל פונקציית מריחת כתם רחבה יותר. גודל פונקציית מריחת הכתם מתכונתי למקדם ההגדלה של המערכת. כלומר הטשטוש אינו גרוע יותר במובן היחסי, אך הוא אכן גרוע יותר במובן המוחלט.
מדידה של פונקציית מריחת הכתם
[עריכת קוד מקור | עריכה]לצורך מדידת פונקציית מריחת הכתם של העדשה, לא נדרש מקור אור נקודתי השולח גל כדורי מושלם לכל עבר במרחב. זאת ממאחר והעדשה מעבירה רוחב סרט (זוויתי) מוגבל. כלומר מקור בעל רוחב סרט גדול מרוחב הסרט שמעבירה העדשה (מאיר מעבר לזווית שנפרשת בין ציר העדשה לקצותיה), לא יתרום יותר ממקור אחר בעל רוחב סרט השווה לזה שמעבירה העדשה. המשמעות היא שניתן להסתפק במקור אור עם רוחב סרט זוויתי בעל רוחב סרט השווה לפחות לזה שמעבירה העדשה שבוחנים (כמובן שהוא צריך להיות אחיד בתחום זה). במילים אחרות, נדרש מקור אור נקודתי הנוצר מגל כדורי (אחיד) מתכנס, שמחצית מהזווית המקסימלית תהיה גדולה מהזווית שנוצרת בין הציר המרכזי לקצה העדשה.
באופן מעשי, רזולוציה אינטרינזית מוגבלת של מערכת הדימות תגרום לכך שפונקציית פיזור הנקודות שתמדד לא תהיה נקיה מאי-ודאות.[3] בעת ביצוע ההדמיה, רצוי להנחית את אונות הצד של אלומת הדמות על ידי שימוש באפודיזציה. במקרה של מערכת דימות שמעבירה אלומה גאוסית, פונקציית מריחת הכתם מתוארת על ידי המשווה הבאה:[4]
כאשר הוא מקדם התלוי ביחס הקטימה וברמת ההארה, הוא Numerical Aperture (בעברית: מפתח נומרי), היא מהירות האור, הוא תדר של פוטון במערכת הדימות, היא העוצמה של אלומת הייחוס, ו- הוא מקדם התאמה והמיקום הרדיאלי ממרכזה של האלומה עבור מישור עבור מסויים.
היסטוריה ושיטות
[עריכת קוד מקור | עריכה]הדיפרקציה (בעברית: עקיפה) נחקרה לראשונה על ידי ג'ורג' בידל איירי במאה ה-19. באותו זמן הוא פיתח ביטוי לאמפליטודה והעוצמה של הפונקציית מריחת הכתם עבור מכשיר מדידה אידיאלי, נקי מאברציות אופטיות (היוצרות דיסקת איירי). את התאוריה לפונקציית מריחת כתם בעלת אברציות בקרבת המוקד האופטמלי חקרו פריץ זרניקה (Frits Zernike) ובן ניג'בור (Ben Nijoboer) בשנות ה-30 וה-40 של המאה העשרים. פולינומי זרניקה, אשר פותחו על ידי זרניקה, לקחו חלק מרכזי בניתוח שביצעו השניים. זאת מכיוון שפולינומים אלו אפשרו ייצוג יעיל של אברציות במערכות אופטיות בעלות סימטריה סיבובית. תוצאות אנליטיות מהשנים האחרונות אפשרו להרחיב את הגישה של זרניקה ו-Nijboer להערכת פונקציית מריחת הכתם לנפחים גדולים בסביבת המוקד האופטימלי. ההרחבה לניתוח של זרניקה ו-Nijboer, הנקראת תאורית ENZ (Extended Nijboer-Zernike Theory) מאפשרת את חקר ההדמיה הלא אידיאלית של עצמים תלת ממדיים במיקרוסקופיה קונפוקלית ובאסטרונומיה בתנאים לא אידיאליים. השימוש בתאורית ENZ נמצא בשימוש גם באפיון אברציות של מכשירים, על ידי מדידת הפילוג של העוצמה דרך המוקד ופתרון הבעיה ההופכית.
שימושים
[עריכת קוד מקור | עריכה]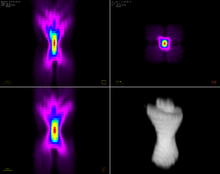
מיקרוסקופיה
[עריכת קוד מקור | עריכה]טשטוש מהווה בעיה חמורה במיקרוסקופיה, לצורך הפחתתו נעשה שימוש בדה קונבולוציה. פונקציית מריחת הכתם נחוצה לצורך שימושה, ועל כן היא בעלת חשיבות רבה.
לצורך אפיון ניסיוני של פונקציית מריחת הכתם במיקרוסקופיה נדרשים עצמים זעירים הקטנים מסף הרזולוציה (דמויי נקודה) שישמשו כמקור אור נקודתי. משום כך נעשה שימוש בנקודות קוונטיות ונקודות פלורסנטיות למטרות אלו.[5][6] עבור עצמים שאינם כה זעירים עשויים לפזר אור באופן שאינו אחד, ובכך לפגוע בדיוק פונקציית מריחת הכתם. במקרים אלו נעשה שימוש במודלים תאורטיים כפי שתוארו לעיל, ואלו מאפשרים חישובים מדויקים של פונקציית מריחת הכתם תחת תנאי דימות רבים.
אסטרונומיה
[עריכת קוד מקור | עריכה]באסטרונומיה תצפיתית, האפיון הניסיוני של פונקציית מריחת הכתם הוא לרוב פשוט, מאחר וקיימים מקורות אור נקודתיים רבים כגון כוכבים וקוואזורים (Quasars). צורתה ומקורה של פונקציית מריחת הכתם עשוי להשתנות באופן ניכר, כתלות במכשיר המדידה ובמטרה שלשמה הוא נמצא בשימוש.
בטלסקופ רדיו, הגורם הדומיננטי המשפיע על פונקציית מריחת הכתם ניתן לזיהוי על ידי הקונפיגורציה של המפתח במישור פוריה. בפועל, עשויים להיות מספר גורמים שנוצרים מאלמנטים שונים במערכת אופטית מורכבת שישפיעו על פונקציית מריחת הכתם. תאור מלא של פונקציית מריחת הכתם יכלול בנוסף תופעות של דיפוזיה של האור (פוטו-אלקטרונים) בגלאי, בנוסף לשגיאת עקיבה בטלסקופ או בכלי ההנושא את הטלסקופ. בטלסקופים אופטיים ההנמצאים על פני הקרקע, מערבולות אטמוספריות (ראיה אסטרונומית) משפיעה באופן ניכר על פונקציית מריחת הכתם. בהדמיה ברזולוציה גבוהה על פני הקרקע, פונקציית מריחת הכתם תשתנה עם המיקום על העצם (תופעה זו נקראת באנגלית anisoplanatis). במערכות אופטיקה אדפטיבית המבוססות על פני האדמה פונקציית מריחת הכתם תהיה שילוב של מפתח המערכת עם שאריות לא מתוקנות של גורמים אטמוספריים.[7]


ליטוגרפיה
[עריכת קוד מקור | עריכה]פונקציית מריחת הכתם היא גבול טבעי עבור הדמיה קונבנציונלית של חריר,[8] עם גבול הדפסה מינימלי הנמצא בין 0.6-0.7 של של מערכת הדימות.[9][10] לדוגמה במערכת EUV (Extreme Ultraviolet) עם אורך גל של 13.5 ננומטרים ו- , ממדי החריר הקטנים ביותר שניתן לבצע להם הדמיה יהיו בטווח של 25-29 ננומטרים. מסכת הזזת פאזה היא בעלת שוליים המוסיפים 180 מעלות לפאזה, ועל ידי כך מאפשרים רזולוציה עדינה יותר.[8]
אופטלמולוגיה
[עריכת קוד מקור | עריכה]בשנים האחרונות חלה התקדמות משמעותית בפיתוח אופטיקה אדפטיבית, והם נמצאים בשימוש בתחום האופתלמולוגיה. הפיתוחים מאפשרים כעת לחשב בדיוק רב את פונקציית מריחת הכתם של העין האנושית, ובכך הופכים אותה לכלי אבחון יעיל ומדויק.
פונקציית מריחת הכתם מאפשרת לרופא מטפל לבחון טיפולים שונים לעינו של המטופל, ולחזות כיצד כל אחד מהם ישפיע על גלגל העין. בנוסף, מידיעת הפונקציה ניתן לתכנן פתרונות שימזערו אותה, ובכך לבצע דימות in vivo למבנים אנטומיים זעירים כגון פוטורצפטורים.[11]
ראו גם
[עריכת קוד מקור | עריכה]- תגובת הלם
- פונקציית תמסורת אופטית
- מערכת ליניארית
- מערכת אופטית
- דיסקת איירי
- פונקציית תמסורת
- דה קונבולוציה
- רזולוציה
קישורים חיצוניים
[עריכת קוד מקור | עריכה]הערות שוליים
[עריכת קוד מקור | עריכה]קטגוריה:אופטיקה קטגוריה:ראייה ממוחשבת
- ^ Rafael C. Gonzalez, Richard E. Woods, 5, Digital Image Processing, 4th Edition, Pearson, 2017, עמ' 350. (בenglish)
- ^ Kiarash Ahi, Mehdi Anwar, Developing terahertz imaging equation and enhancement of the resolution of terahertz images using deconvolution, Proc. SPIE 9856, Terahertz Physics, Devices, and Systems X: Advanced Applications in Industry and Defense, 98560N, Terahertz Physics, Devices, and Systems X: Advanced Applications in Industry and Defense 9856, May 26, 2016, עמ' 98560N doi: 10.1117/12.2228680
- ^ Kiarash Ahi, Sina Shahbazmohamadi, Navid Asadizanjani, Quality control and authentication of packaged integrated circuits using enhanced-spatial-resolution terahertz time-domain spectroscopy and imaging, Optics and Lasers in Engineering 104, July 2017, עמ' 274–284 doi: 10.1016/j.optlaseng.2017.07.007
- ^ K. Ahi, Mathematical Modeling of THz Point Spread Function and Simulation of THz Imaging Systems, IEEE Transactions on Terahertz Science and Technology, 6 7, November 2017, עמ' 747–754 doi: 10.1109/tthz.2017.2750690
- ^ Light transmitted through minute holes in a thin layer of silver vacuum or chemically deposited on a slide or cover-slip have also been used, as they are bright and do not photo-bleach. Light transmitted through minute holes in a thin layer of silver vacuum or chemically deposited on a slide or cover-slip have also been used, as they are bright and do not photo-bleach. S. Courty; C. Bouzigues; C. Luccardini; M-V Ehrensperger; S. Bonneau & M. Dahan (2006). "Tracking individual proteins in living cells using single quantum dot imaging". In James Inglese (ed.). Methods in Enzymology: Measuring biological responses with automated microscopy, Volume 414. Academic Press. pp. 223–224. ISBN 9780121828196.
- ^ P. J. Shaw & D. J. Rawlins (August 1991). "The point-spread function of a confocal microscope: its measurement and use in deconvolution of 3-D data". Journal of Microscopy. 163 (2): 151–165. doi:10.1111/j.1365-2818.1991.tb03168.x.
- ^ POINT SPREAD FUNCTION (PSF)
- ^ 1 2 The Natural Resolution
- ^ Corner Rounding and Line-end Shortening
- ^ Principles and Practice of Light Microscopy
- ^ Austin Roorda, Fernando Romero-Borja, William J. Donnelly Iii, Hope Queener, Thomas J. Hebert, Melanie C. W. Campbell, Adaptive optics scanning laser ophthalmoscopy, Optics Express, 9 10, 2002-05-06, עמ' 405–412 doi: 10.1364/OE.10.000405

































