עדשה

ערך זה עוסק ברכיב אופטי. אם התכוונתם למשמעות אחרת, ראו עדשה (פירושונים).

סוגי עדשות

דמותו של האסטרונאוט קלייטון אנדרסון משתקפת דרך טיפת מים, המרחפת עקב חוסר משקל ומתפקדת כעדשה מרכזת.

עדשה היא רכיב אופטי (לרוב שקוף) המשמש להסטת קרני אור ויצירת תופעות אופטיות של מיקוד או פיזור של אור. עדשות עשויות בדרך כלל מזכוכית שעברה תהליכי עיבוד שנועדו למטרה מוגדרת. השם עדשה שאול מעולם הצומח בהיות צורתה דומה לזרעי עדשים.

עדשות הן רכיב הכרחי במכשירים רבים ומגוונים, בעיקר אמצעים אופטיים כמו מצלמה, מיקרוסקופ, טלסקופ, משקפת זכוכית מגדלת וכדומה. מכשירי הדמיה שאינם אופטיים כגון מיקרוגלים, שפופרת קרן קתודית (מסך CRT) ומיקרוסקופ אלקטרוני משתמשים למיקוד קרינה שאינה אור (מיקרוגל או אלקטרונים) באביזרים בעלי תפקוד דומה לעדשה האופטית, אך כמובן שונים מהותית.

גם בתוך העין נמצאת עדשה, עדשת העין, המשמשת לריכוז קרני האור ומיקודן על הרשתית. עדשה זו משנה את עוצמתה ובהתאם מתאימה את המיקוד שלה על ידי שרירים המשנים את צורתה.

סוגים של עדשות

עדשה מרכזת

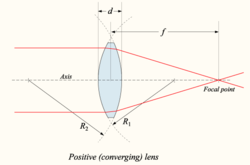
• עדשה מרכזת היא עדשה הממקדת קרני אור מקבילות במישור המוקד שלה. דוגמה לעדשה כזו היא עדשת המצלמה.
  • עדשה קמורה משני צידיה ממקדת את הקרניים במוקד הנמצא במרחק מה ממנה, בצד ההפוך לצד קליטתן. כגודל הקימור כך מרחק המוקד מהעדשה.
• עדשה מפזרת היא עדשה המסיטה קרניים מקבילות כך שהמשכיהן יפגשו במישור המוקד שלה.
  • עדשה קעורה משני צידיה מפזרת את הקרניים הנכנסות. מוקד העדשה נמצא בצד כניסת הקרניים במרחק מה מהעדשה.
• עדשת מניסקוס היא עדשה שבה לרדיוסים אותו סימן (-/+) והיא יכולה להיות מרכזת או מפזרת.

תכונות של עדשות

אורך המוקד של העדשה הוא המרחק של הנקודה שאליה מתרכזות קרניים מקבילות לציר העדשה. גם ההפך מתקיים, כל קרן שתצא מנקודת המוקד ותעבור בעדשה תהיה מקבילה לציר העדשה.

מספר f של העדשה הוא אורך המוקד שלה חלקי קוטר המפתח שלה והוא קובע את בהירות הדמות המתקבלת.

עוצמת העדשה היא אחד חלקי מרחק המוקד, ונמדדת בדרך כלל בדיופטר, שהוא אחד חלקי מטר, והיא מהווה מדד לכושר השבירה של העדשה.

חישוב עצמה של עדשה עבה

ערך מורחב – נוסחת לוטשי העדשות

עדשה מפזרת

על מנת למצוא את העצמה של עדשה, משתמשים לעתים קרובות בנוסחת לוטשי העדשות:

$\ D= \frac{1}{f} = \left(\frac{n_1}{n_2}-1\right) \left[ \frac{1}{R_1} - \frac{1}{R_2} + \frac{(n_1-1)d}{n_1 R_1 R_2} \right]$

כאשר:

D- עצמת העדשה.

f-מרחק מוקד העדשה.

n₁- מקדם השבירה של החומר ממנו עשויה העדשה.

n₂- מקדם השבירה מחוץ לעדשה.

R1- רדיוס המשטח הראשון.

R2- רדיוס המשטח השני.

d- עוביה של העדשה במרכזה.

פעמים רבות מזניחים את עביה של העדשה המרכזת (0=d). כמו כן העדשה נמצאת באוויר כך שגורם השבירה מחוץ לעדשה הוא 1 (1=n₂) ואז המשוואה נראית כך:

$\ D= \frac{1}{f} = \left(n_1-1\right) \left[ \frac{1}{R_1} - \frac{1}{R_2} \right]$

הדמיית עצם דרך עדשה מרכזת דקה

עדשה מרכזת

כדי למצוא באופן גרפי דמות של עצם דק המאונך לציר האופטי שבסיסו נמצא על ציר המערכת נחפש את הדמות של קצה העצם ונניח שהדמות מאונכת לציר האופטי. מקום הדמות של נקודה היא נקודת המפגש של כל הקרניים שיוצאות מהנקודה המתאימה בעצם. ישנן שלוש קרניים שקל לצייר את מהלכן דרך העדשה:

• קרן שיוצאת מראש הגוף, מקבילה לציר פוגעת בעדשה וסוטה כך שהיא עוברת דרך המוקד.
• קרן שפוגעת במרכז העדשה וממשיכה במסלולה ללא סטייה.
• קרן שיוצאת מראש הדמות, עוברת דרך המוקד, פוגעת בעדשה וסוטה כך שהיא מקבילה לציר.

בדרך כלל משתמשים בשתיים מהקרניים דלעיל כדי למצוא את מקום הדמות.

ניתן כמו כן למצוא את מקום הדמות באופן חישובי באמצעות הנוסחה:

$\frac{1}{f} = \frac{1}{U} + \frac{1}{V}$

$\ U = \ S_o + \ f$

$\ V = \ S_i + \ f$

$\ M= \frac{V}{U} = \frac{H_i}{H_o} = \frac{f}{S_o} = \frac{S_i}{f}$

$\ S_o S_i = \ f^2$

$\ U$ - מרחק העצם מהעדשה (שמאל=חיובי, ימין=שלילי)

$\ V$ - מרחק הדמות מהעדשה (ימין=חיובי, שמאל=שלילי)

$\ f$ - אורך המוקד של העדשה (מרכזת=חיובי, מפזרת=שלילי)

$\ S_o$ - מרחק העצם מהמוקד

$\ S_i$ - מרחק הדמות מהמוקד

$\ H_o$ - אורך העצם

$\ H_i$ - אורך הדמות

$\ M$ - ההגדלה/ההקטנה

הגדלה, הרחקה, הפיכה וממשות

בעדשה מרכזת נבחין בין 5 מקרים:

גוף נמצא במרחק גדול מפעמיים מרחק המוקד

• גוף נמצא במרחק גדול מפעמיים מרחק המוקד (u>2f). הדמות שנוצרה היא:
  • קטנה יותר מהגוף.
  • קרובה יותר לעדשה מהגוף.
  • הפוכה יחסית לגוף.
  • הדמות ממשית.

גוף נמצא במרחק שווה לפעמיים מרחק המוקד

• גוף נמצא במרחק שווה לפעמיים מרחק המוקד (u=2f). הדמות שנוצרה היא:
  • שווה בגודלה לגוף.
  • שווה במרחקה מהעדשה כמו הגוף.
  • הפוכה יחסית לגוף.
  • הדמות ממשית.

גוף נמצא בין מרחק המוקד לפעמיים מרחק המוקד

• גוף נמצא בין המוקד לפעמיים המוקד (2f>u>f). הדמות שנוצרה היא:
  • גדולה יותר מהגוף.
  • רחוקה יותר מהעדשה לעומת הגוף.
  • הפוכה יחסית לגוף.
  • הדמות ממשית.

גוף נמצא במרחק המוקד

• גוף נמצא במרחק שווה למרחק המוקד (u=f). הקרניים לא יפגשו אף פעם ולכן לא תיווצר דמות.

גוף נמצא במרחק קטן ממרחק המוקד

• גוף נמצא בין העדשה למוקד (u<f). הדמות שנוצרה היא:
  • גדולה יותר מהגוף.
  • רחוקה יותר מהעדשה לעומת הגוף.
  • ישרה יחסית לגוף.
  • הדמות מדומה.

בעדשה מפזרת נבחין בין 5 מקרים:

גוף נמצא במרחק גדול מפעמיים מרחק המוקד

• גוף נמצא במרחק גדול מפעמיים מרחק המוקד (u>2f), הדמות שנוצרה היא:
  • קטנה יותר מהגוף.
  • קרובה יותר לעדשה מהגוף.
  • ישרה יחסית לגוף.
  • הדמות מדומה.

גוף נמצא במרחק שווה לפעמיים מרחק המוקד

• גוף נמצא במרחק שווה לפעמיים מרחק המוקד (u=2f). הדמות שנוצרה היא:
  • קטנה יותר מהגוף.
  • קרובה יותר לעדשה מהגוף.
  • ישרה יחסית לגוף.
  • הדמות מדומה.

גוף נמצא בין מרחק המוקד לפעמיים מרחק המוקד

• גוף נמצא בין המוקד לפעמיים המוקד (2f>u>f). הדמות שנוצרה היא:
  • קטנה יותר מהגוף.
  • קרובה יותר לעדשה מהגוף.
  • ישרה יחסית לגוף.
  • הדמות מדומה.

• גוף נמצא על המוקד (u=f). הדמות שנוצרה היא:
  • קטנה יותר מהגוף.
  • קרובה יותר לעדשה מהגוף.
  • ישרה יחסית לגוף.
  • הדמות מדומה.

גוף נמצא במרחק קטן ממרחק המוקד

• גוף נמצא בין העדשה למוקד (u<f). הדמות שנוצרה היא:
  • קטנה יותר מהגוף.
  • קרובה יותר לעדשה מהגוף.
  • ישרה יחסית לגוף.
  • הדמות מדומה.

לסיכום: בעדשה מפזרת הדמות תמיד ישרה, מוקטנת ומדומה.

ראו גם

• עין
• מצלמה
• משקפיים
• עדשות מגע
• אובייקטיב
• עדשת פרנל- עדשה דקה וקלה יותר העשויה טבעות טבעות.
• עדשת GRIN- עדשה המבוססת על גורם שבירה משתנה (gradient index).
• עדשה אקוסטית.
• עדשה א-ספרית.