אופטיקת פורייה
אופטיקת פורייה היא ענף באופטיקה שהחל להתפתח בסוף המאה ה-19. תורה זו מתארת את מהלך האור על ידי שימוש במכניקת הגלים ובכלים מתמטיים, הלקוחים מהנדסת חשמל ומתורת האינפורמציה. היא מהווה כלי חישובי ותאורטי פופולרי בקרב פיזיקאים ומהנדסים כיום והיא שימושית מאוד באופטיקה, תקשורת, מכ"ם ועוד. קרויה על שמו של המתמטיקאי והפיזיקאי הצרפתי ז'אן-בטיסט ז'וזף פורייה ועל שם ההתמרה האינטגרלית הנושאת את שמו - התמרת פורייה.

רקע היסטורי[עריכת קוד מקור | עריכה]
אופטיקה גלית[עריכת קוד מקור | עריכה]
עד המאה ה-19 נהגו פיזיקאים לתאר את האור כזרם של חלקיקים. גישה זו נקבעה במאה ה-17 על ידי אייזק ניוטון והולידה את האופטיקה הגאומטרית אשר נלמדת עד היום ומצליחה להסביר בצורה מדויקת למדי הרבה תופעות אופטיות "יומיומיות". למרות הצלחתה של האופטיקה הגאומטרית, במאה ה-19 גילו פיזיקאים כמו אוגוסטן ז'אן פרנל, יוזף פראונהופר, תומאס יאנג ואחרים כי האור עובר תופעות גליות של התאבכות ועקיפה, אשר אינן ניתנות להסבר על ידי המודל החלקיקי והאופטיקה הגאומטרית. לעומת זאת, תופעות אלה בהחלט ניתנות להסבר על ידי אימוץ התפיסה כי האור הוא גל המתפשט במרחב. בכך נזנח המודל הניוטוני של האופטיקה הגאומטרית לטובת האופטיקה הגלית. גישה פיזיקלית חדשה זו יכולה הייתה להסביר הן את התופעות המוכרות של האופטיקה הגאומטרית והן את התופעות, שבאותה עת נחשבו חדשות, של עקיפה והתאבכות. תורה זו הגיעה לבשלות בשנת 1864, עת הציג הפיזיקאי הסקוטי ג'יימס קלרק מקסוול בפני החברה המלכותית סט של ארבע משוואות דיפרנציאליות המתארות את התנהגות הגלים האלקטרומגנטיים. משוואות אלו מכונות היום "משוואות מקסוול" והן מהוות את הבסיס התאורטי לכל התיאור הגלי של האור.
על אף יעילותה ורב-גוניותה של האופטיקה הגלית, היו עוד כמה תופעות שלא ניתנות היו להסבר גם על ידה. אחת מהן הייתה הקטסטרופה באולטרה-סגול של קרינת גוף שחור והשנייה הייתה האפקט הפוטואלקטרי. ארבעים ואחת שנים מאוחר יותר, בשנת 1905, הציע אלברט איינשטיין הסבר לאפקט הפוטואלקטרי על ידי אימוץ מודל חלקיקי חדש לאור, אולם טען כי אין בכך כוונה לזנוח את ההנחה כי האור הוא גם גל. גישה זו, המקבלת שני מודלים שונים ונפרדים (המודל החלקיקי והמודל הגלי) בו-זמנית, נקראת היום "הדואליות של האור" והיא מניחה כי לאור יש גם תכונות גליות אשר מתוארות היטב על ידי המודל הגלי וגם תכונות חלקיקיות המתוארות היטב על ידי המודל החלקיקי. גישה זו הולידה בתחילת המאה ה-20 את המכניקה הקוונטית, אשר הצמיחה את האופטיקה הקוונטית, המתארת את התנהגות אור במערכות מסדר גודל קטן מאוד - גודל שבו נכשלת האופטיקה הגלית.
אף על פי שהאופטיקה הקוונטית מתארת את התנהגות האור בצורה טובה יותר מהאופטיקה הגלית, פשטותה היחסית של האופטיקה הגלית ויעילותה בתיאור תופעות אופטיות בשלל בעיות הנדסיות ופיזיקליות הופכים אותה לכלי חשוב ושימושי למהנדסים ומדענים גם כיום.
אופטיקה, תקשורת ואינפורמציה[עריכת קוד מקור | עריכה]
מאז שנות השלושים של המאה ה-20, הייתה התקרבות של פיזיקאים רבים העוסקים באופטיקה לענפי האינפורמציה והתקשורת מתחום הנדסת החשמל. מגמה זו מובנת לאור העובדה כי קיים דמיון רב בין מערכות תקשורת ומערכות הדמיה, בשני המקרים מטרתן היא לאסוף ולהוביל מידע. כלומר, שני סוגי המערכות מקבלים מידע (קלט) ופולטים מידע (פלט). עבור מערכות תקשורת המידע הוא בדרך כלל פונקציה זמנית (מתח או זרם התלויים בזמן) ועבור מערכות אופטיות המידע הוא פונקציה מרחבית (התפלגות מרחבית של עצמת האור או של אמפליטודת השדה האלקטרומגנטי). יתרה מזאת, מערכות תקשורת ומערכות אופטיות חולקות תכונות נוספות כמו ליניאריות ואינווריאנטיות. כל מערכת בעלת שתי תכונות אלו ניתנת לתיאור מתמטי על ידי ניתוח תדירויות ואנליזת פורייה.
עם התחזקותה של טכנולוגיית המחשוב (הגידול בכוח החישוב והזיכרון, הוזלתם ומיזעורם של המחשבים ופיתוח אלגוריתמים מהירים) נעשתה אנליזת פורייה קלה, פשוטה ונגישה יותר. עובדה זו תרמה להפיכתה של אנליזת פורייה לכלי מתמטי נפוץ בקרב קהילת האלקטרו-אופטיקאים.
רקע מתמטי[עריכת קוד מקור | עריכה]
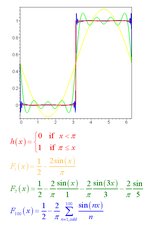
הבסיס התאורטי לאופטיקת פורייה נובע מענף במתמטיקה הנקרא "טוריי פורייה". לפי תורה זו, בהתקיימם של תנאים מסוימים, ניתן לרשום כל פונקציה כטור של פונקציות הרמוניות (סינוסים וקוסינוסים). פונקציות הרמוניות אלה מקיימות את משוואת הגלים ולכן גם כל צירוף ליניארי שלהן מקיים אותה. לפיכך, אם נסתכל על אות כלשהו שמציית למשוואת הגלים (גל אור, אות חשמלי), מורכב ככל שיהיה, ניתן יהיה לפרק אותו לסדרה של רכיבים - סינוסים וקוסינוסים פשוטים הנקראים "רכיבי פורייה". על רכיבים אלה ניתן לעשות מניפולציות בצורה פשוטה יחסית - פעולה זאת נקראת "עיבוד האות". לאחר עיבוד האות מרכיבים את כל הרכיבים מחדש ליצירת הפלט (תמונה במקרה של מערכת אופטית או אות חשמלי במקרה של מערכת תקשורת).
הפעולה המתמטית שמפרקת את הקלט לרכיביו נקראת התמרת פורייה והפעולה שמחברת את רכיבי פורייה מחדש נקראת "התמרת פורייה ההפוכה". עדשה מבצעת את התמרת פורייה על גל אור שנכנס אליה.

התמרת פורייה דו-ממדית[עריכת קוד מקור | עריכה]
לאורך הערך כולו נשתמש בהגדרה הבאה עבור התמרת פורייה של פונקציה דו־ממדית :
כאשר היא היחידה המדומה, נקראות התדירויות המרחביות ויש להן יחידות הפוכות ליחידות של .
את ההתמרה ההפוכה נגדיר באופן הבא:
לשתי התמרות אינטגרליות אלה תכונות שימושיות כמו ליניאריות, הפרדת משתנים וסימטריה והן מצייתות למספר משפטים מתמטיים שכדאי לקורא להכיר כמו משפט פרסבל, משפט הקונבולוציה, משפט אינטגרל פורייה ועוד.
בנוסף, נציג את התמרת הנקל מסדר אפס, שהיא התמרת אנלוגית להתמרת פורייה המתאימה לפונקציות דו־ממדיות עם סימטריה רדיאלית
:
כאשר היא פונקציית בסל מסדר אפס ונתונה ע"י:
בשלב זה נמליץ לקורא ללמוד ולהכיר התמרות פורייה/הנקל של פונקציות שימושיות (מדרגת היחידה, מפתח ריבועי, מפתח מעגלי, פונקציית דלתא של דיראק, פונקציית "אוהל", רכבת הלמים וכו'), אשר לא הובאו כאן כדי לא להכביד על קריאת הערך.
מערכות ליניאריות[עריכת קוד מקור | עריכה]
מערכת מוגדרת כמיפוי של סט נתוני קלט לסט נתוני פלט. עבור המקרה של מערכות חשמליות, הקלט והפלט הוא פונקציית חד־ממדיות של הזרם או המתח התלויות בזמן; עבור המקרה של מערכות אופטיות, הקלט והפלט הן פונקציות דו־ממדיות ממשיות (עוצמה) או מרוכבות (השדה) המשתנות במרחב. נסמן את פעולת המערכת על ידי אופרטור מתמטי הפועל על פונקציית הקלט וממפה אותה לפונקציה
באופן הבא:

מתוך קבוצת כל האופרטורים נתמקד רק באופרטורים הליניאריים. ליניאריות של אופרטור אומרת שהפלט מאופרטור הפועל על קומבינציה ליניארית של שתי פונקציות (או יותר) הוא קומבינציה ליניארית של פלט האופרטור לאחר שפעל על כל פונקציה בנפרד. או בכתיב מתמטי - עבור כל שתי פונקציות
ועבור כל שני סקלרים
מתקיים:
.}

ליניאריות ואינטגרל הסופרפוזיציה[עריכת קוד מקור | עריכה]
נסתכל על פעולת אופרטור ליניארי הפועל על פונקציית כניסה . אך מעט לפני כן, נשתמש בתכונה ידועה של פונקציית-דלתא כדי לכתוב את פונקציית הכניסה בצורה הבאה:
.
למציאת התגובה של המערכת יש להפעיל את האופרטור על הקלט
.
משום שהאופרטור לא פועל על פונקציית משתני-הדמה שבאינטגרל, ניתן להכניס אותו לתוך האינטגרל ולהפעילו על פונקציית הדלתא בלבד
.
בשלב הסופי, נגדיר את פונקציית התגובה להלם של המערכת
.
כעת, ניתן לרשום את הקשר בין הקלט והפלט של המערכת הליניארית באופן הבא
.
אינטגרל זה נקרא "אינטגרל הסופרפוזיציה" וחשוב לשים לב אינטגרל זה הוא בעצם קונבולוציה. ובכך אנו מקבלים עקרון חשוב מאוד באופטיקת פורייה - הפלט של מערכת אופטית שווה לקונבולוציה של פונקציית הכניסה עם פונקציית התגובה להלם של המערכת .
כאן ראוי להזכיר את משפט הקונבולוציה הטוען כי התמרת פורייה של קונבולוציה בין שתי פונקציות שווה למכפלת התמרות פורייה של כל פונקציה בנפרד (בהנחה שתנאי המשפט מתקיימים) - . כאשר
היא התמרת פורייה של פונקציית הפלט
והפונקציה
היא התמרת פורייה של פונקציית הקלט
והפונקציה
היא התמרת פורייה של פונקציית התגובה להלם של המערכת והיא נקראת גם פונקציית התמסורת של המערכת.
מעבר ממשוואות מקסוול הווקטוריות למשוואת הלמהולץ הסקלרית[עריכת קוד מקור | עריכה]
כאמור, הבסיס לכל המודל הגלי של האור מסוכם בצורה אלגנטית ופשוטה על ידי ארבעת משוואות מקסוול. משוואות אלו הן משוואות דיפרניציאליות וקטורית והן מצמדות בין השדה החשמלי והשדה המגנטי. עבור תווך ליניארי, איזוטרופי, הומוגני, לא נפיץ ולא-מגנטי משוואות מקסוול יכולות להכתב בצורה הבאה (במערכת יחידות MKS)
.
לפי זהות וקטורית שימושית מתקיים:
.
אם נציב בזהות זו את המשוואת השלישית ונציב אותה מחדש במשוואת מקסוול הראשונה, נקבל את משוואת הגלים עבור השדה החשמלי
.
כש- הוא מקדם השבירה של החומר ו- היא מהירות האור בריק.
משוואה וקטורית זו ניתנת להפרדה לרכיבים - כל רכיב של השדה החשמלי, , מציית למשוואה זו בנפרד ולכן ניתן לפרק אותה לסט של שלוש משוואות סקלריות כאשר
.
משום שכל גל ניתן לכתיבה על ידי סכום של גלים מישוריים מהצורה
בעלי וקטורי-גל
שונים, יש טעם להציב את הגל המישורי במשוואת הגלים.
לשם כך יש לחשב את הנגזרת הזמנית ולהציבה במשוואת הגלים :
.
לאחר הכנסת יחס הדיספרסיה המתאים לתווך איזוטרופי והומוגני מקבלים את המשוואה
.
(תהליך דומה ניתן לעשות גם עבור השדה המגנטי).
משוואה זו נקראת משוואת הלמהולץ והיא הייתה מוכרת למהנדסי החשמל שעסקו בקווי תמסורת ובתקשורת טלגרף.
היתרון של עבודה עם משוואה זו במקום עם משוואת הגלים הוא שכעת אין פותרים משוואה עם תלות זמנית ומרחבית, אלא משוואה מרחבית בלבד.
דיפרקציה במרחב חופשי[עריכת קוד מקור | עריכה]
הבעיה הבסיסית באופטיקה היא זו - נתונה פונקציית ההתפלגות של האמפליטודת השדה האלקטרומגנטי במישור הכניסה למערכת. נניח כי הגל הוא מונוכרומטי (בעל אורך גל בודד
) ומתקדם בכיוון ציר z. פונקציית הכניסה היא
.
אנו מחפשים את פונקציית התפלגות השדה ביציאה מהמערכת, שבמקרה הנוכחי היא מרחב חופשי,
, כאשר השדה מציית למשוואת הלמהולץ.
לפי עקרון הויגינס-פרנל, כל נקודה בפונקציית הכניסה היא מקור של גל כדורי, כאשר
נותנת את המשקל של כל מקור כזה. לפיכך, פתרון הבעיה הוא סופרפוזיציה של גלים כדוריים, אשר לכל אחד מהם מקבל משקל שונה:
.
קירוב פרנל[עריכת קוד מקור | עריכה]
כאשר גודל המפתח של פונקציית הכניסה קטן מספיק ממרחק ההתקדמות של הגל, ניתן לקרב את השורש שבאקספוננט לפי טור טיילור באופן הבא:
לאחר הכנסת קירוב זה לאקספוננט שבאינטגרל מקבלים:
.
בשלב זה ניתן לסמן
.
בנוסף, אפשר להבחין כי האינטגרל הנ"ל, המכונה גם אינטגרל הדיפרקציה של פרנל-כירכהוף, הוא למעשה התמרת פורייה של הפונקציה
.
נרשום זאת כך:
.
קירוב פראנהופר[עריכת קוד מקור | עריכה]
כאשר מרחק ההתקדמות גדול מספיק כדי לקרב את האקספוננט
ל-1, אנו נותרים בלעדיו באינטרגרנד ואינטגרל פרנל-כירכהוף הופך להיות התמרת פורייה של
. כך מקבלים:
.
כאשר:
.
משום שהעצמה תלויה בריבוע ערכה המוחלט של האמפליטודה ניתן לכתוב את התמונה ביציאה כך:
.
קירוב זה נקרא קירוב פראנהופר ובו טמון העיקרון החשוב ביותר באופטיקת פורייה והסיבה לשמה:
פונקציית היציאה מהמערכת היא התמרת פורייה של פונקציית הכניסה.
דוגמאות[עריכת קוד מקור | עריכה]
עקיפה ממפתח מלבני[עריכת קוד מקור | עריכה]

במשטח מישורי מחומר אטום לאור, קיים חור מלבני בעל רוחב a וגובה b המואר בתאורה אחידה. נחשב כאן את תמונת המפתח על מסך המרוחק מרחק z מן המפתח, לפי קירוב פראנהופר:
ראשית, נרשום את פונקציית הכניסה -
.
לפי קירוב פראנהופר, כדי לחשב את פונקציית היציאה צריך למצוא את התמרת פורייה של הכניסה. במקרה זה היא:
.
כאשר:
.
והעוצמה תהיה:
עקיפה ממפתח עגול[עריכת קוד מקור | עריכה]

נחשב את התמונת ביציאה מהמערכת כשהמפתח הוא מעגלי בקוטר l. פונקציית הכניסה הפעם היא:
.
כאשר
הפעם נשתמש בהתמרת הנקל לחישוב פונקציית היציאה.
כש-A הוא שטח המעגל ו-
עם
.
עצמת השדה ביציאה במקרה זה תהיה:
עקיפה מסריג אמפליטודה סינוסואידי[עריכת קוד מקור | עריכה]

במקרה זה פונקציית הכניסה היא סינוס עם תדירות מרחבית
לאורך ציר x ועומק מודולציה
ה"רוכב" על עוצמה קבועה בת יחידה אחת:
.
במקרה זה התמרת פורייה של הכניסה תיתן:
.
זוהי תוצאה שימושית מאוד - "הולדתן" של שתי פונקציות הדלתא נותנת שניתן להשתמש בסריג אמפליטודה דק כמעין מפצל קרניים - קרן נכנסת מתפצלת לשלוש קרנים: קרן אחת ממשיכה באותה דרך, קרן שנייה המוסטת ימינה וקרן שלישית מוסטת שמאלה. כדי לממש רכיב בעל פעולה דומה ההמסתמך רק על אופטיקה גאומטרית יש לתכנן רכיב עבה, כבד ומסורבל.
באופן דומה, ניתן לתכנן רכיב בעל פונקציית שן-מסור שיעשה עבודה דומה (אם כי שם נקבל יותר משתי קרניים) או שן-מסור א-סימטרי, שבאמצעותו ניתן לקבל קרן חדשה אחת בלבד.
זו דוגמה טובה ליתרונותיה של אופטיקת פורייה בתכנון רכיבים אופטיים, ובעיקר בתכנון רכיבים דיפרקטיביים שלא ניתן היה לתכנן באמצעות אופטיקה גאומטרית.
רכיבים דקים[עריכת קוד מקור | עריכה]
בחלק הקודם עסקנו במערכת "מרחב חפשי". בחלק זה נביא רכיבים אופטיים נוספים - אל כולם נתייחס כאל רכיבים "דקים". כלומר, אין בתוכם תופעות דיפרקציה משניות. בנוסף, לשם פשטות החישובים, נתעלם מהחזרות פנימיות ומתופעות לא ליניאריות (אם ישנן).
בדומה לסימונים בחישובי מערכות ליניאריות, מטרתנו היא לבטא את פעולת הרכיב כאופרטור t הפועל על פונקציית הכניסה:
.
לוח דיאלקטרי[עריכת קוד מקור | עריכה]

נסתכל על לוח דיאלקטרי שקוף, בעל מקדם שבירה n ועובי d.
ללא המעבר דרך הלוח, היה האור צובר איבר פאזה
, אך משום שהאור עובר דרך הלוח הוא יקבל איבר פאזה
.
לכן הפרש הפאזה ביחס לאור שהיה עובר בוואקום מכתיב שאופרטור הרכיב יהיה:
.
כאשר הגל פוגע בלוח בזווית
,
אז העובי האפקטיבי של הלוח הוא בקירוב הפראקסיאלי
. אם נציב זאת באופרטור הלוח נקבל:
.
פריזמה[עריכת קוד מקור | עריכה]

נתונה פריזמה דקה (נקראת לפעמים גם "טריז" - wedge), בעלת מקדם שבירה n ובעלת זווית ראש
. נוכל לכתוב ביטוי עבור עובי הלוחית כפונקציה של y:
.
לכן אופרטור הפריזמה יהיה:
.
עדשה דקה[עריכת קוד מקור | עריכה]

נחשב את הביטוי עבור עדשה דקה בעלת עובי מרבי a, מקדם שבירה n ורדיוסי עקמומיות
המצייתים להסכם הסימנים של נוסחת לוטשי-העדשות. לפי נוסחת לוטשי העדשות לעדשה כזו יהיה אורך מוקד
.
באופן דומה לשני הרכיבים הקודמים, נרשום את עובי העדשה ונציב בביטוי עבור הפרש הפאזה בין אור שעבר בעדשה ובין אור שעבר בוואקום:
.
לכן פונקציית ההעברה (או ה"אופרטור") של העדשה תהיה:
.
בביטוי זה ניתן להבחין בשני איברים: האיבר הראשון - איבר פאזה גלובלית קבוע במרחב והוא פחות מעניין מביניהם. האיבר השני - פאזה ריבועית, היוצרת גל כדורי. זהו האיבר הגורם לגל מישורי להתכנס או להתבדר, בהתאם למוקד העדשה ומרחק ההתפשטות.
שיטת האופרטורים[עריכת קוד מקור | עריכה]
לאחר שמצאנו ביטויים עבור רכיבים אופטיים ועבור התקדמות במרחב חופשי, נוכל כעת להרכיב ביטויים עבור מערכות מורכבות יותר, מרובות רכיבים. כפי שניתן לצפות, הביטוי עבור מערכת מרובת מקטעים של התקדמות במרחב חופשי יכול להיות ארוך ומסורבל וידרוש פתרון אינטגרלים רבים. כדי להתמודד עם אתגר זה, נציג נוטציה שימושית:
ראשית, נגדיר אופרטור מתאים לכל רכיב ולאחר מכן נציג את היחסים ביניהם.
נסמן את הגדלים הבאים:
אופרטור קנה-מידה (scaling)[עריכת קוד מקור | עריכה]
אופרטור ההזזה[עריכת קוד מקור | עריכה]
אופרטור הפאזה הריבועית[עריכת קוד מקור | עריכה]
אופרטור עדשה דקה בעלת מוקד f[עריכת קוד מקור | עריכה]
אופרטור ההתקדמות בתווך חופשי[עריכת קוד מקור | עריכה]
כאשר F מציין התמרת פורייה ו- מציין את התמרת פורייה ההפוכה.
יחסי אופרטורים[עריכת קוד מקור | עריכה]
| F | Q | R | ||
|---|---|---|---|---|
| F | ||||
| Q |
| |||
| R |
|
דוגמאות[עריכת קוד מקור | עריכה]
עדשה בודדת - מישור פורייה[עריכת קוד מקור | עריכה]
נתונה עדשה בודדת בעלת אורך מוקד f. נרצה לבדוק מהי הטרנספורמציה שיעבור גל שפוגע בעדשה ומתקדם מרחק של f.
אופרטור המערכת הוא:
.
נרשום את R בצורתו המפורשת:
ונציב בביטוי עבור אופרטור המערכת:
.
ניתן כעת לאחד את שני ה־Q-ים העוקבים ולבטלם. נקבל את הביטוי:
.
מכאן ניתן ללמוד כי לאחר שהאור עובר בעדשה ומתקדם למישור המוקד הוא מקבל איבר פאזה ריבועית (שאינו בא לידי ביטוי בעוצמה) ועובר כיווץ/הגדלה, אך הדבר החשוב ביותר הוא שהאור עובר התמרת פורייה. משום כך קוראים למישור המוקד של העדשה בשם "מישור פורייה". כפי שנראה בהמשך, עובדת היותה של מערכת זו כרכיב שמייצר טרנספורם פורייה של הגל הנכנס תהיה שימושית מאוד לצורכי עיבוד נתונים אנלוגי, למשל עבור סינון מרחבי.
הדמיה על ידי עדשה בודדת[עריכת קוד מקור | עריכה]
נתונה המערכת הבאה: עדשה בעלת מרחק מוקד f מדמה אובייקט המרוחק ממנה מרחק u לתמונה אשר נמצאת במרחק v.
לפי תנאי הדימות מתקיים
.
אופרטור המערכת יהיה:
.
נרשום את האופרטורים R בצורתם המפורשת ונציב בביטוי עבור אופרטור המערכת לקבלת:
.
נשתמש ביחסי האופרטורים בין שני Q-ים עוקבים ובתנאי הדימות עבור שלושת ה־Q-ים שבמרכז:
. איבר זה מתבטל.
אופרטור המערכת הוא כעת:
.
ניתן להזיז את ה-F הראשון מקום אחד ימינה לפי היחס
ולאחר מכן, להשתמש ביחס בין שתי התמרות פורייה עוקבות
לקבלת הביטוי:
.
את שלושת ה
-ים העוקבים ניתן לצמצם ל-
ולהחליף מקום בין ו־Q לקבלת:
.
לבסוף, ניתן לאחד את שני ה־Q-ים לקבלת התוצאה הסופית:
.
מסקנה: מערכת זו, בסה"כ מוסיפה איבר פאזה ריבועית, משנה את קנה-המידה של התמונה (מגדילה או מקטינה) והופכת את התמונה. איבר הפאזה הריבועית לא בא לידי ביטוי בפונקציית העוצמה (העצמה תלויה רק בריבוע ערך המוחלט).
עיבוד אותות אנלוגי[עריכת קוד מקור | עריכה]

טרנפורם פורייה הפועל על פונקציית כניסה מפרק אותה לרכיביה הספקטרליים השונים, כשלכל רכיב כזה יש משקל שונה. כפי שראינו, עדשה יכולה למפות גל נכנס לטרנספורם פורייה שלו במישור המוקד שלה ("מישור פורייה"). משום כך, ניתן לעשות מניפולציות שונות על רכיבי פורייה של פונקציית הכניסה במישור פורייה. למשל, ניתן להנמיך את חלקם, או אפילו לחסום לחלוטין.
למשל, נחשוב על רשת שתי וערב של קווים ישרים: במישור פורייה של עדשה, נקבל את טרנספורם פורייה שלו. במקרה זה - סריג ריבועי של נקודות. על ידי הצבת צמצם אופקי נוכל לחסום את כל התדרים השייכים לרכיבי פורייה בעלי מחזוריות בכיוון y ולאפשר רק לחלק מרכיבי פורייה בעלי מחזוריות בכיוון x לעבור. כעת נציב עדשה נוספת. עדשה זו תמפה את התמונה במישור פורייה לטרנספורם פורייה שלה במישור המוקד של העדשה החדשה. כלומר, מפעילים את התמרת פורייה פעמיים וחוזרים לתמונה המקורית, אך הפעם ללא הרכיבים בעלי המחזוריות בציר y, אלא רק בציר x. כך ניתן לקבל את קווי האורך בלבד. באופן דומה, על ידי הוספת צמצם אורכי במישור פורייה, נוכל לסנן את קווי האורך ולקבל את קווי הרוחב בלבד.
הטכניקה אינה מוגבלת רק לתמונות מחזוריות. ניתן לסנן באמצעותה רעשים, לחסום תדרים גבוהים (הממוקמים רחוק מהראשית במישור פורייה) או תדרים נמוכים (הממוקמים קרוב לראשית), או להעביר תחום תדרים סופי. לשם כך עלינו רק לחסום פיזית נקודות במישור פורייה.
מערכות אופטיות בעלות מפתח סופי[עריכת קוד מקור | עריכה]

עד עתה, כל הרכיבים האופטיים נחשבו כרכיבים אינסופיים בשטחם. כאשר לרכיבים יש גודל סופי, למשל עבור עדשה בעלת מפתח מעגלי בקוטר d, גודלם הסופי משפיע על התמונה ביציאה כפי שנראה בדוגמה הבאה.
כאמור, נתבונן בגל הנפלט מאובייקט, הנמצא מרחק u משמאל לעדשה סופית בעלת מוקד f ומפתח סופי המיוצג על ידי הפונקציה
, אשר ממופה לתמונה במישור במרחק v מימין לעדשה. אופרטור המערכת במקרה זה ניתן לביטוי ע"י
. כאשר לפי תנאי הדימות מתקיים
.
לאחר הצבה של הביטוי המפורש של R, תנאי הדימות וקצת אלגברת אופרטורים נקבל:
.
לפי חוקי התמרת פורייה ומשפט הקונבולוציה מתקבל הביטוי הסופי:
.
כאשר
היא התמרת פורייה של פונקציית המפתח p ו-
הוא סימן הקונבולוציה.
ניתן לראות כי פעולת המערכת נותנת פונקציית יציאה שמורכבת מקונבולוציה של התמרת פורייה של פונקציית המפתח, שבמקרה של עדשה עגולה היא פונקציית בסל, עם פונקציית הכניסה לאחר שעברה כיווץ/הרחבה. ישנם גם איברי פאזה ריבועית שאותם ניתן לבטל בקלות על ידי הוספת עדשות בעלות אורך מוקד של u ו-v במישור הכניסה ובמישור היציאה בהתאמה. אם העדשה הייתה אינסופית אז פונקציית המפתח שלה הייתה מישור אינסופי, שהתמרת הפורייה שלו היא פונקציית דלתא. הקונבולוציה של פונקציית דלתא עם פונקציית הכניסה היא פונקציית הכניסה בעצמה. זו התוצאה שקיבלנו כשחישבנו את פעולת עדשה אינסופית.
הארה לא קוהרנטית[עריכת קוד מקור | עריכה]
עד כה טיפלנו במערכות אופטיות ליניאריות המוארות בתאורה קוהרנטית.
קיבלנו שעבור מערכות אלו הפלט הוא קונבולוציה של הקלט עם פונקציית התגובה להלם של המערכת
ושהעוצמה ביציאה היא
.
מערכת המוארת בתאורה לא קוהרנטית תהיה ליניארית בעוצמה ולא באמפליטודה כמו במקרה הקוהרנטי. העוצמה במוצא תהיה קונבולוציה של עוצמת התגובה להם עם עוצמת פונקציית הכניסה:
.
לשם נוחות, נהוג להפעיל את משפט הקונבולוציה כדי לעבוד עם מכפלה במקום קונבולוציה:
.
עוד נהוג לנרמל את כל הפונציות לפי ערכן בראשית:
ולרשום את הנוסחה הנ"ל בצורה:
.
הפוקציה
נקראת "פונקציית התמסורת הלא קוהרנטית" או "פונקציית תמסורת אופטית" של המערכת (Optical Tranfer Function - OTF) ויש לה משמעות גאומטרית:
עבור שני מפתחים שאחד נמצא במיקום
והשני נמצא במקום
, כאשר v הוא המרחק למישור המוקד, פונקציית התמסורת האופטית מייצגת את היחס בין שטח החפיפה של שני המפתחים ובין השטח הכולל של שניהם.
כושר הפרדה - הגבלת רזולוציה אופטית[עריכת קוד מקור | עריכה]
כאמור, סופיותו וצורתו של המפתח של המערכת האופטית משפיעים על התמונה ביציאה בכך שהתמונה היא קונבולוציה של התמרת פורייה של המפתח עם פונקציית הכניסה. עובדה זו, יוצרת בעיה של הבחנה בין שתי נקודות שונות במישור הכניסה. כשהעדשה הייתה אינסופית היא הייתה יכולה למפות שתי נקודות (פונקציות דלתא) שונות במישור הכניסה לשתי נקודות (פונקציות דלתא) שונות במישור היציאה. כלומר, הייתה לצופה המתבונן בתמונה אפשרות להבחין בין שתי נקודות שונות ולייחס אותן לשתי נקודות שונות במישור הכניסה. לשם הדוגמה, נחשוב על שני כוכבים רחוקים. מערכת אופטית בעלת מפתח אינסופי הייתה יכולה למפות את שניהם לנקודות שונות על גלאי, כך שצופה היה יכול להבין כי אלו הם שני כוכבים שונים. כאשר למערכת מפתח סופי, שתי נקודות במישור הכניסה ימופו לשתי פונקציות סופיות (למשל, במקרה של מפתח עגול - לשתי פונקציות Airy). משום שלפונקציות אלה יש רוחב, אם הן יהיו "קרובות מדי" הן יכולות להראות כמו פונקציה אחת "מרוחה" על פני השטח והצופה לא יוכל להבדיל אם זהו כתם או שתי נקודות מובדלות. אם נישאר עם דוגמת הכוכבים, אז צופה לא יוכל להבחין כי אלו שני כוכבים נפרדים ויטעה לחשוב כי זהו גוף אחד גדול.
בעיה זו נקראת בעיית הרזולוציה האופטית. הפיזיקאי זוכה פרס נובל לורד ריילי קבע קריטריון לקביעת רזולוציה אופטית של מערכת אופטית, הנקרא קריטריון ריילי. ריילי קבע כי שני מקורות נקודתיים הם "מופרדים" על ידי מערכת אופטית בעלת מפתח עגול בעל קוטר D כאשר המרחק בין שני שיאי תבניות Airy של שני המקורות שווה למרחק של האפס הראשון של פונקציית Airy ממרכזה.
דוגמה 1: הפרדה בין שני מקורות נקודתיים - הארה קוהרנטית[עריכת קוד מקור | עריכה]
נתונה מערכת אופטית בעלת מפתח עגול ברדיוס R ושני מקורות נקודתיים וקוהרנטיים המרוחקים במרחק
זה מזה.
מפתח המערכת מבוטא על ידי הביטוי הבא:
והתמרת הפורייה שלה היא הפונקציה:
כש-
.
התפלגות האמפילטודה בכניסה תבוטא כך:
.

התמונה המתקבלת במישור פורייה של המערכת נתונה ע"י:
כש- v הוא מרחק העדשה ממישור התמונה, u הוא המרחק בין האובייקט והעדשה ו-M היא ההגדלה הליניארית
.
חישוב הקונבולוציה נותן:
כש-
הוא פולינום בסל מסדר ראשון.
(מן הגרף המצורף, ניתן לראות כי האפס הראשון של פונקציית בסל מסדר 1 הוא בערך
.
העוצמה ביציאת מהמערכת תהיה אם כן-
כאשר עובדים בתאורה קוהרנטית ישנה אפשרות להגביר את כושר ההפרדה. אם ניתן להוסיף איבר פאזה שרירותי לאחר המקורות, אז פונקציית העצמה תהיה:
.
כפי שנראה בקרוב, במקרה של הפרש פאזה
ניתן להגביר את כושר ההפרדה של המערכת - השדה במרכז תמיד מתאפס ולכן תמיד ניתן יהיה להבחין בין שני המקורות.
דוגמה 2: הפרדה בין שני מקורות נקודתיים - הארה לא-קוהרנטית[עריכת קוד מקור | עריכה]
בהינתן אות המערכת ואותה הבעיה כמו בדוגמה הקודמת אך הפעם - עם תאורה לא-קוהרנטית, פונקציית העצמה ביציאה מהמערכת היא סכום ריבועי תבניות איירי:
השוואה בין כושר ההפרדה של מערכת עם תאורה קוהרנטית לעומת תאורה לא-קוהרנטית[עריכת קוד מקור | עריכה]
הגרפים באנימציה מתארים את חתך פונקציית העצמה של תמונת שני מקורות נקודתיים המרוחקים ביניהם במרחקים שונים כפי שתיראה דרך מערכת אופטית עם מפתח סופי. המעגלים האדומים מציינים את המיקום המדויק של תמונת המקורות במערכת אידיאלית. ניתן לראות כי לפי קריטריון ריילי, דווקא תאורה לא-קוהרנטית עדיפה על תאורה קוהרנטית בכושר ההבחנה בין שני המקורות. עבור תאורה קוהרנטית, שני השיאים השייכים לשני המקורות מתאבכים לכדי שיא אחד במרחקים גדולים יותר מאשר כשהמקורות לא קוהרנטיים. בנוסף, עבור תאורה לא קוהרנטית מיקום השיאים קרוב יותר למיקמם אם המערכת הייתה אידיאלית.
הגרף התחתון מתאר שני מקורות קוהרנטיים עם הפרש פאזה של בניהם. ניתן ללמוד מגרף זה שהשדה בין שני המקורות תמיד מתאפס ולכן תמיד ניתן להפריד בניהם, אולם, היתרון בכושר ההפרדה במקרה זה בא עם החיסרון של חוסר דיוק במיקום.

לקריאה נוספת[עריכת קוד מקור | עריכה]
- Goodman, Joseph W. "Introduction to Fourier optics." 1968


![{\displaystyle {\mathcal {F}}\left\{g_{(x,y)}\right\}=G_{(f_{x},f_{y})}=\int _{-\infty }^{+\infty }{\int _{-\infty }^{+\infty }{g_{(x,y)}{\mbox{exp}}\left[-j2\pi \left(f_{x}x+f_{y}y\right)\right]}\,dx}\,dy}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbedbf921ab3fab67f204474d7aef0488fdb22f3)



![{\displaystyle {\mathcal {F}}^{-1}\left\{G_{(f_{x},f_{y})}\right\}=g_{(x,y)}=\int _{-\infty }^{+\infty }{\int _{-\infty }^{+\infty }{G_{(f_{x},f_{y})}{\mbox{exp}}\left[j2\pi \left(f_{x}x+f_{y}y\right)\right]}\,df_{x}}\,df_{y}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4f96aa9690bc0f0373a147b69b1e78f45ea2f98)



![{\displaystyle J_{0}\left(a\right)={\frac {1}{2\pi }}\int _{0}^{2\pi }{{\mbox{exp}}\left[-ja\cos \left(\theta -\phi \right)\right]}\,d\theta }](https://wikimedia.org/api/rest_v1/media/math/render/svg/fde366827d310bdf47f065493b027a9628030b27)






























![{\displaystyle {\vec {u}}\left({\vec {r}};t\right)={\vec {u}}_{0}{\mbox{exp}}\left[\pm j\left({\vec {k}}\cdot {\vec {r}}-\omega t\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e9323807c7d3c7eed51008703254d3b6f239b222)








![{\displaystyle u_{1}\left(x_{1},y_{1},z\right)={\frac {1}{j\lambda z}}\int {\int {u_{0}\left(x_{0},y_{0},z\right){\mbox{exp}}\left[j{\frac {2\pi }{\lambda }}{\sqrt {\left(x_{1}-x_{0}\right)^{2}+\left(y_{1}-y_{0}\right)^{2}+z^{2}}}\right]}\,dx_{0}}\,dy_{0}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9ab4c863210220a8fedc14efd69946e2e330106)



















![{\displaystyle I_{out}=4{\frac {A^{2}}{\lambda ^{2}z^{2}}}\left[{\frac {J_{1}\left(\pi \rho l\right)}{\pi \rho l}}\right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68474c1444063eac503edb79ab4e3311df885431)



![{\displaystyle u_{out}=\Omega {\mathcal {F}}\left\{u_{in}\right\}=\Omega \left[\delta \left(f_{x},f_{y}\right)+{\frac {m}{2}}\delta \left(f_{x}-f_{0},f_{y}\right)+{\frac {m}{2}}\delta \left(f_{x}+f_{0},f_{y}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ae1e03a90fd8d6a8384113d8653f6bf05254a14)











![{\displaystyle f=\left[\left(n-1\right)\left({\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}\right)\right]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a516bfb9f95a3a2a14fd214cf3d32e3b8b89a51)



![{\displaystyle \nu [a]f(x,y)=f(ax,ay)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/46fb6000ba9e0037dbfee8e802e98b032c87df51)
![{\displaystyle S[{\vec {s}}]f(x,y)=f(x-s_{x},y-s_{y})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5105d4235bd94f4f7b60266b43b055ca5ab933c2)
![{\displaystyle Q[a]=e^{{\frac {k}{2}}a\rho ^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25db3915ffaf1e32cb1402a4080848c6ef6bf013)
![{\displaystyle Q[-1/f]=e^{l{\frac {k}{2}}\left(-{\frac {1}{f}}\right)\rho ^{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb3522899cac4da6ac504edd4f9f8103ce0d9cd6)
![{\displaystyle R[z]={\frac {e^{jkz}}{jkz}}Q[1/z]\nu [1/\lambda z]FQ[1/z]=e^{jkz}F^{-1}Q[-\lambda ^{2}z]F}](https://wikimedia.org/api/rest_v1/media/math/render/svg/560574245356e4a0cfb0dc541d96955792d60880)


![{\displaystyle \nu [t_{2}]\nu [t_{1}]=\nu [t_{2}t_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/261dbcdc010982a3fe5b9daa5f4da760b6cbf248)
![{\displaystyle \nu [t]F=F\nu [1/t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a3091d202e2ea4a6f40e33c258bc15966040525)
![{\displaystyle \nu [t]Q[c]=Q[t^{2}c]\nu [t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb37a78b80a0b8654b18423ede30698b95d2d967)
![{\displaystyle \nu [t]R[d]=R[d/t^{2}]\nu [t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c86225aa17ea1b48a737afc8830ed372f2e023ee)
![{\displaystyle F\nu [t]=\nu [1/t]F}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d21d48108d85dc727be882c2b758a20e07b21aa5)
![{\displaystyle FF=\nu [-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5a67d6a62f381cbf40f8c75cd61c4fb2667dcb7)
![{\displaystyle FQ[c]=R\left[{\frac {-c}{\lambda ^{2}}}\right]F}](https://wikimedia.org/api/rest_v1/media/math/render/svg/73e175ba0df9f0923d9430b8a38dd7d9d56b3f44)
![{\displaystyle FR[d]=Q[-\lambda ^{2}d]F}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38fe675d9932350f7d4edc2d9189c38743bd818a)
![{\displaystyle Q[c]\nu [t]=\nu [t]Q[c/t^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b90a31efe2a6c3c2be78105119bd4409e3e42fee)
![{\displaystyle Q[c]F=FR[-c/\lambda ^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fc85d85de396a3c4aba11b7755cdf861596c885)
![{\displaystyle Q[c_{2}]Q[c_{1}]=Q[c_{2}+c_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24714506927c330e7e789f7d19f303783285afbc)
![{\displaystyle Q[c]R[d]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9dd5923c4958c0f42d4509a39fc37a42e059c124)
![{\displaystyle R\left[(d^{-1}+c)\right]^{-1}\cdot }](https://wikimedia.org/api/rest_v1/media/math/render/svg/e57c31273a5abef8f7138401aaf8235fabf63aef)
![{\displaystyle \nu [1+cd]\cdot }](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce47676e33d8c4c5a026d103de2650085fd2420a)
![{\displaystyle Q\left[(c^{-1}+d)^{-1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5802c139bbd500792f8f32614fd5fb965c87e26)
![{\displaystyle R[d]\nu [t]=\nu [t]R[t^{2}d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cddf98affd0fe80317ece6a91608c45caba10e59)
![{\displaystyle R[d]F=FQ[-\lambda ^{2}d]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ad99ab49023ec5ceb0419f87f35318753e67f5a)
![{\displaystyle R[d]Q[c]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/209dd90ec97c3fc5946ddb7b87656a335c60e7ad)
![{\displaystyle Q\left[(c^{-1}+d)^{-1}\right]\cdot }](https://wikimedia.org/api/rest_v1/media/math/render/svg/43fe5e7c6fe4260bf20bf511c5fe085a4b5d9a1c)
![{\displaystyle \nu \left[(1+cd)^{-1}\right]\cdot }](https://wikimedia.org/api/rest_v1/media/math/render/svg/d8152fab90f04dae454bdfb2884a0c7f573fe9fb)
![{\displaystyle R\left[(d^{-1}+c)^{-1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48978cfb5e7f4695ed5d671ab115d04b3c5d5428)
![{\displaystyle R[d_{2}]R[d_{1}]=R[d_{2}+d_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c80fd8f99e30b9c3b1b44b6083c9aa534804b0c4)
![{\displaystyle \tau =R[f]Q\left[-{\frac {1}{f}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bccde076735331ae713af6e6cb13ad449e1eca8)
![{\displaystyle R[f]=Q\left[{\frac {1}{f}}\right]\nu \left[{\frac {1}{\lambda f}}\right]FQ\left[{\frac {1}{f}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/711455fb3e7bac698844f9198ff0ea6fdb2313cc)
![{\displaystyle \tau =Q\left[{\frac {1}{f}}\right]\nu \left[{\frac {1}{\lambda f}}\right]FQ\left[{\frac {1}{f}}\right]Q\left[-{\frac {1}{f}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c19e1149bfc9d6f5a9d45da4c7675dba009f46a)
![{\displaystyle \tau =Q\left[{\frac {1}{f}}\right]\nu \left[{\frac {1}{\lambda f}}\right]F}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dec9f9f0da391002b0681f85dfeb3b402a4a469e)

![{\displaystyle \tau =R[v]Q\left[-{\frac {1}{f}}\right]R[u]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d11d584704072aa13ddf83fa59f86fb2075324d)
![{\displaystyle \tau =Q\left[{\frac {1}{v}}\right]\nu \left[{\frac {1}{\lambda v}}\right]FQ\left[{\frac {1}{v}}\right]Q\left[-{\frac {1}{f}}\right]Q\left[{\frac {1}{u}}\right]\nu \left[{\frac {1}{\lambda u}}\right]FQ[\left[{\frac {1}{u}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/725a041f44f0e4e0efbda82b421a4429f37c4c02)
![{\displaystyle Q\left[{\frac {1}{v}}\right]Q\left[-{\frac {1}{f}}\right]Q\left[{\frac {1}{u}}\right]=Q\left[{\frac {1}{v}}+{\frac {1}{u}}-{\frac {1}{f}}\right]=Q[0]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c9b586eff07a74be412bab36fa27ec256092f5f4)
![{\displaystyle \tau =Q\left[{\frac {1}{v}}\right]\nu \left[{\frac {1}{\lambda v}}\right]F\nu \left[{\frac {1}{\lambda u}}\right]FQ[\left[{\frac {1}{u}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4018ce7e7ad51356d04d61eec605768961f653b1)
![{\displaystyle F\nu \left[{\frac {1}{\lambda u}}\right]=F\nu \left[\lambda u\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20969401aab15cb98700c924104aa7017c6e9f3d)
![{\displaystyle \tau =Q\left[{\frac {1}{v}}\right]\nu \left[{\frac {1}{\lambda v}}\right]\nu \left[-1\right]\nu \left[\lambda u\right]Q\left[{\frac {1}{u}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cb4d2d6ff88a7b9a4c76f6cbbd8d2bf993744ff)
![{\displaystyle \nu \left[-{\frac {u}{v}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abbeab3592e1dab4e0115f16fbecf3084b5b9bc6)
![{\displaystyle \tau =Q\left[{\frac {1}{v}}\right]Q\left[{\frac {u}{v^{2}}}\right]\nu \left[-{\frac {u}{v}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fde0cef98a71b33d96bad800e6fa6b64e90a5a3)
![{\displaystyle \tau =Q\left[{\frac {u+v}{v^{2}}}\right]\nu \left[-{\frac {u}{v}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/248d420076a7012ff5e0fa4d741ab187c6ce016d)

![{\displaystyle \tau =R[v]\cdot p(x,y)Q\left[-{\frac {1}{f}}\right]R[v]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ba8cbbf2f59ed3dcd618afb58b11f769d405f9a)
![{\displaystyle u_{out}=\tau u_{in}\approx Q\left[{\frac {1}{v}}\right]\nu \left[{\frac {1}{\lambda f}}\right]F\left\{p(x,y)\cdot F\nu \left[\lambda v\right]Q\left[{\frac {1}{u}}\right]u_{in}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2e72894d3051b2d295971daa6e9b5ddc423f949a)
![{\displaystyle u_{out}\approx Q\left[{\frac {1}{v}}\right]\nu \left[{\frac {1}{\lambda f}}\right]\left\{P(f_{x},f_{y})*\nu \left[-\lambda v\right]Q\left[{\frac {1}{u}}\right]u_{in}\right\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f13db3c9a459a8f1893735b75be5a2afaac3ea0)



























