אנרגיה פוטנציאלית חשמלית

אנרגיה פוטנציאלית חשמלית היא אנרגיה פוטנציאלית האצורה בשדה חשמלי, הנובעת מכוח לורנץ הפועל על מטען חשמלי בשדה אלקטרומגנטי. יחידת ה-SI של אנרגיה פוטנציאלית חשמלית היא ג'אול.

אנרגיה פוטנציאלית של חלקיק טעון

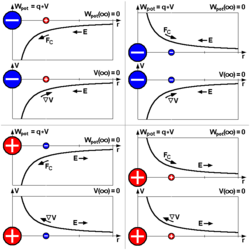
האנרגיה החשמלית נובעת מהימצאותו של מטען חשמלי בתוך שדה חשמלי. האנרגיה הפוטנציאלית החשמלית של חלקיק q המצוי בפוטנציאל חשמלי $\ V(r)$ שווה למכפלה $\ qV(r)$. העבודה הנדרשת להעברת מטען זה דרך הפרש פוטנציאלים נתון על ידי המשוואה הבאה: $W_{ab} = qV_{ab} = q(V_{a}-V_{b}) \,$

אנרגיה פוטנציאלית האצורה בקבוצת מטענים

האנרגיה הפוטנציאלית בין שני מטענים שווה לאנרגיה הפוטנציאלית של אחד המטענים בהשפעת השדה החשמלי שיוצר המטען השני. כלומר, אם מטען $q_1$ יוצר בנקודה $r_2$ בה מונח מטען $q_2$ פוטנציאל חשמלי $V_{r_2}$, אז האנרגיה הפוטנציאלית האצורה תהיה: $U = q_2V_{r_2}$. ניתן היה לחשב את האנרגיה גם על פי הפוטנציאל בנקודה $r_1$, ולכן ברור שמתקיים: $U = q_1V_{r_1} = q_2V_{r_2} = \frac{1}{2}(q_1V_{r_1}+q_2V_{r_2})$

ביטוי זה ניתן להכללה עבור קבוצה של $N$ מטענים $q_i$ הממוקמים בנקודות $r_i$, כאשר בכל אחת מנקודות אלו יש פוטנציאל של $V_{r_i}$ שנוצר בהשפעת כל המטענים פרט למטען הנמצא בנקודה $r_i$. הביטוי עבור המקרה הכללי הוא: $U = \frac{1}{2}\sum_{i=1}^N q_iV_{r_i}$

הערה: ההכפלה בחצי נועדה לפצות על ספירה כפולה של ההשפעה ההדדית בין כל שני מטענים.

אנרגיה פוטנציאלית האצורה בפילוג מטען מרחבי

ניתן להכליל שוב את הביטוי מהסעיף הקודם כדי לקבל ביטוי עבור האנרגיה הפוטנציאלית של פילוג מטען שאינו מורכב בהכרח מאוסף מטענים נקודתיים אלא מרוח על פני המרחב:

$U = \frac{1}{2}\int \limits_{\text{all space}} \rho(r)V(r)d^3r$

כאשר:

$\ \rho(r)$ היא צפיפות המטען של הפילוג בנקודה $r$.

$\ V(r)$ הוא הפוטנציאל החשמלי בנקודה $r$.

אנרגיה האצורה בשדה חשמלי

ניתן להשתמש במשוואה של האנרגיה הפוטנציאלית האצורה בפילוג מטען מרחבי ולהביאה למונחים של השדה החשמלי.

על פי חוק גאוס (בצורתו הדיפרנציאלית): $\mathbf{\nabla}\cdot\vec E = \frac{\rho(r) }{\epsilon_r\epsilon_0}$

כאשר:

$\epsilon_r$ הוא המקדם הדיאלקטרי היחסי של התווך.

$\epsilon_0$ הוא המקדם הדיאלקטרי של הריק.

$\vec E$ הוא וקטור השדה החשמלי.

לכן מתקיים:

$U = \frac{1}{2}\int \limits_{\text{all space}} \rho(r)V(r)d^3r = \frac{1}{2}\int \limits_{\text{all space}} \epsilon_r\epsilon_0(\mathbf{\nabla}\cdot{\vec {E}})V(r)d^3r$

עפ"י חוקי אנליזה וקטורית:

$\mathbf{\nabla}\cdot(\vec EV) = (\mathbf{\nabla}V)\vec E + V(\mathbf{\nabla}\cdot\vec E)$

ולכן:

$U = \frac{\epsilon_r\epsilon_0}{2}\int \limits_{\text{all space}} \mathbf{\nabla}\cdot(\vec EV) d^3r - \frac{\epsilon_r\epsilon_0}{2}\int \limits_{\text{all space}} (\mathbf{\nabla}V)\vec E d^3r$

תוך שימוש במשפט גאוס וקביעה שהפוטנציאל החשמלי באינסוף מתאפס:

$U = \frac{\epsilon_r\epsilon_0}{2}\int V\vec E\cdot \vec {dA} - \frac{\epsilon_r\epsilon_0}{2}\int \limits_{\text{all space}} (-\vec E)\cdot\vec E d^3r = \int \limits_{\text{all space}} \frac{1}{2}\epsilon_r\epsilon_0\left|{\vec E}\right|^2 d^3r$

לכן, צפיפות האנרגיה, או האנרגיה ליחידת נפח של השדה החשמלי היא: $\eta = \frac{1}{2} \epsilon_r\epsilon_0 \left|E\right|^2$

ראו גם

• אנרגיה
• אנרגיה פוטנציאלית