משפט תאלס

במתמטיקה, קיימים שני משפטים המכונים בשם 'משפט תאלס' על שמו של תאלס איש מילטוס.

המשפט הראשון

משפט תאלס הפשוט

בגאומטריה האוקלידית, משפט תאלס קובע שישרים מקבילים חותכים מצד אחד של שוקי זווית קטעים בעלי יחסים שווים. למשל, בציור שמשמאל, אם $DE \| BC$ , אז $\frac{AB}{AD}=\frac{AC}{AE}$

על פי חוקי פרופורציה, ניתן להגיע לשוויונות נוספים, כמו $\frac{AD}{DB}=\frac{AE}{EC}$ או $\frac{AB}{DB}=\frac{AC}{EC}$

הרחבות

הרחבה ראשונה

הרחבה ראשונה

כאמור, משפט תאלס הפשוט מתייחס רק למקרה שבו הישרים המקבילים נמצאים מאותו צד של קודקוד הזווית. ההרחבה הראשונה קובעת שמשפט תאלס נכון גם אם הישרים אינם מאותו צד של קודקוד הזווית (כמו בציור משמאל).

הרחבה שנייה

ההרחבה השנייה קובעת שגם היחס בין הקטעים שהזווית חותכת מהישרים המקבילים, שווה ליחס בין החלקים שהישרים המקבילים חותכים משוקי הזווית, כלומר $\frac{AB}{AD}=\frac{AC}{AE}=\frac{BC}{DE}$

הוכחת המשפט

המשפט עצמו

מעבירים את $\ BE$ ואת $\ CD$.

בוחנים את המשולש $\ BDE$ ואת המשולש $\ CDE$.

בשני משולשים אלו, $\ DE$ צלע, והגובה מ-$\ B$ ל-$\ DE$ שווה לגובה מ-$\ C$ ל-$\ DE$. (כי $DE\|BC$)

לכן, שטחי משולשים אלו שווים, כלומר $\ S_{BDE}=S_{CDE}$

אם מוסיפים לשני האגפים את שטח המשולש $\ ADE$, מקבלים $\ S_{ABE}=S_{ACD}$

מחלקים את שני האגפים בשטח המשולש $\ ADE$, ומקבלים $\frac{S_{ABE}}{S_{ADE}}=\frac{S_{ACD}}{S_{ADE}}$

מורידים גובה $\ h_1$ מ-$\ E$ ל-$\ AB$, וגובה $\ h_2$ מ-$\ D$ ל-$\ AC$.

מכיוון ששטח משולש שווה למחצית מכפלת צלע בגובה לה, נקבל: $\frac {\frac{h_1AB}{2}} {\frac{h_1AD}{2}} = \frac {\frac{h_2AC}{2}} {\frac{h_2AE}{2}}$

לאחר צמצום, מקבלים: $\frac{AB}{AD}=\frac{AC}{AE}$

הרחבה ראשונה

מעבירים את $\ BE$ ואת $\ CD$.

בוחנים את המשולש $\ BDE$ ואת המשולש $\ CDE$.

בשני משולשים אלו, $\ DE$ צלע, והגובה מ-$\ B$ ל-$\ DE$ שווה לגובה מ-$\ C$ ל-$\ DE$. (כי $DE\|BC$)

לכן, שטחי משולשים אלו שווים, כלומר $\ S_{BDE}=S_{CDE}$

אם מורידים משני האגפים את שטח המשולש $\ ADE$, מקבלים $\ S_{ABE}=S_{ACD}$

מחלקים את שני האגפים בשטח המשולש $\ ADE$, ונקבל $\frac{S_{ABE}}{S_{ADE}}=\frac{S_{ACD}}{S_{ADE}}$

מורידים גובה $\ h_1$ מ-$\ E$ ל-$\ AB$, וגובה $\ h_2$ מ-$\ D$ ל-$\ AC$.

מכיוון ששטח משולש שווה למחצית מכפלת צלע בגובה לה, מקבלים: $\frac {\frac{h_1AB}{2}} {\frac{h_1AD}{2}} = \frac {\frac{h_2AC}{2}} {\frac{h_2AE}{2}}$

לאחר צמצום, מקבלים: $\frac{AB}{AD}=\frac{AC}{AE}$

הרחבה שנייה

על הקטע $\ BC$, מסמנים נקודה $\ M$, כך ש-$\ DE=MC$. מכיוון ש-$\ DE=MC$ וש-$DE\|MC$,‏ $\ DECM$ מקבילית, ולכן $DM\|EC$

לכן, על פי משפט תאלס, (כאשר מתייחסים לזווית $\angle ABC$) $\frac{BC}{MC}=\frac{AB}{AD}$

נציב$\ DE=MC$, ונקבל $\frac{BC}{DE}=\frac{AB}{AD}$

המשפט השני

משפט תאלס: $\ B$ היא זווית ישרה

בגאומטריה האוקלידית, משפט תאלס קובע שהזווית המונחת על קוטר במעגל היא זווית ישרה: אם הנקודות $\ A$ ,$\ B$ ו-$\ C$ מונחות על מעגל והקו $\ AC$ עובר דרך מרכז המעגל, אז הזווית $\ \angle ABC$ שווה לתשעים מעלות.

משפט זה היה ידוע ככל הנראה באופן אמפירי כבר למצרים והבבלים, אבל הם לא עסקו בהוכחות גאומטריות, וממילא לא סיפקו הוכחה גם למשפט זה. ההוכחה הראשונה מיוחסת לפילוסוף והגאומטרן היווני תאלס ממילטוס, שעל-שמו קרוי המשפט.

הוכחת המשפט

ההוכחה מסתמכת על שתי עובדות ידועות, שגם אותן מייחס אוקלידס (ב"יסודות") לתלס.

• זוויות הבסיס במשולש שווה-שוקיים, שוות זו לזו.
• סכום הזוויות במשולש שווה למאה ושמונים מעלות.

הוכחת משפט תלס

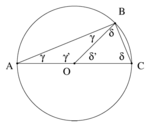
נסמן ב-$\ O$ את מרכז המעגל. מכיוון שהנקודות $\ A$ ,$\ B$ ו-$\ C$ מונחות על המעגל, מתקיים $\ OA=OB=OC$, ולכן המשולשים $\ OAB$ ו-$\ OBC$ שניהם שווי-שוקיים. לפי העובדה הראשונה שהוזכרה לעיל, $\ \angle OBC=\angle OCB$ וכן $\ \angle BAO=\angle ABO$. נסמן את הזווית הראשונה באות $\ \delta$, ואת השנייה באות $\ \gamma$. סכום הזויות במשולש ABC הוא $\ 2\delta+2\gamma=180^{\circ}$, ואם נחלק את שני האגפים בשניים ונקבל $\ \gamma+\delta=90^{\circ}$.

ניסוח סימטרי והכללה

המשפט, כפי שהוצג כאן, קובע שאם משולש חסום במעגל באופן שאחת מצלעותיו היא קוטר, אז המשולש הוא ישר-זווית. גם ההיפך נכון, וכך אפשר לנסח את המשפט באופן סימטרי:

• המרכז של מעגל החוסם משולש מונח על אחת הצלעות, אם ורק אם המשולש ישר-זווית.

משפט תאלס הוא מקרה פרטי של המשפט שלפיו זווית מרכזית המונחת על מיתר במעגל כפולה תמיד מן הזווית ההיקפית.