המרחב המשיק
יש להשלים ערך זה: בערך זה חסר תוכן מהותי. ייתכן שתמצאו פירוט בדף השיחה.
| ||
| יש להשלים ערך זה: בערך זה חסר תוכן מהותי. ייתכן שתמצאו פירוט בדף השיחה. | |
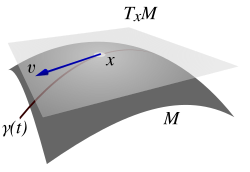
המרחב המשיק בגאומטריה דיפרנציאלית הוא מרחב וקטורי שנבנה על יריעה חלקה ומתפקד כ"קירוב ליניארי" של אותה יריעה באופן מקומי, במובן זה, שהוא מתאר את הכיוונים השונים שבהם ניתן להתקדם על היריעה. לכל נקודה על היריעה יש מרחב משיק משלה שמסומן ב אבל הואיל וכל המרחבים המשיקים הם מרחבים וקטורים באותו ממד, הם איזומורפיים זה לזה.
הגדרה[עריכת קוד מקור | עריכה]
הגדרה על ידי נגזרות כיווניות[עריכת קוד מקור | עריכה]
במרחב האוקלידי למונח "הכיוונים השונים שבהם ניתן להתקדם מהנקודה" יש פירוש אינטואיטיבי כמרחב כל הנגזרות הכיווניות בנקודה. זהו מרחב וקטורי שאיזומורפי למרחב האוקלידי עצמו (על ידי האיזומורפיזם הטבעי שמעביר את הנגזרת הכיוונית לפי הווקטור v לווקטור v עצמו). את מרחב הנגזרות הכיוונות בנקודה p ניתן להציג כאוסף של פונקציונלים:
משמעות התנאי היא ש-v הוא פונקציונל ליניארי על מרחב הפונקציות החלקות (), שמקיים בנוסף לליניאריות תנאי גזירה מסוים (שלעיתים מכונה "כלל לייבניץ") לגבי הפעולה שלו על מכפלה. אוסף זה מכונה המרחב המשיק בנקודה p ואיבריו מכונים וקטורים משיקים. ניתן לראות מההגדרה של האוסף שהוא מרחב ליניארי ומקיים, לפי כלל לייבניץ, שלכל וקטור משיק , כלומר כל הווקטורים המשיקים מתאפסים על פונקציות קבועות.
ההצגה הזו שנראית אולי מסורבלת במרחב האוקלידי מאפשרת ליצור הכללה ליריעות דיפרנציאליות כלליות בצורה טבעית ביותר- ביריעה M המרחב המשיק בנקודה p, הוא האוסף הבא:
כאשר הוא אוסף הפונקציות החלקות על היריעה M. כמו במרחב האוקלידי זהו מרחב וקטורי בעל ממד ששווה לממד היריעה.
אם מערכת קואורדינטות מקומיות בנקודה p אז הווקטורים המשיקים הם בסיס למרחב המשיק בנקודה (כאשר הם מוגדרים ו- ti הוא הציר ה-i-י במערכת הצירים ב- ).
ביריעות שגזירות רק k פעמים (כלומר שלכל שתי מפות הפונקציה גזירה k פעמים אבל לא בהכרח חלקה) ההגדרה הנ"ל יכולה ליצור מרחב מממד אינסופי ולכן מגדירים את המרחב המשיק ביריעות האלו כמרחב שנפרש על ידי הווקטורים המשיקים שמוגדרים באותה צורה.
הגדרה על ידי מסילות חלקות[עריכת קוד מקור | עריכה]
ניתן להגדיר את המרחב המשיק מכיוון יותר גאומטרי: אם נלך לאורך קו מסוים על היריעה (שניתן על ידי עקומה חלקה) וניקח פונקציה חלקה כלשהי, אז לאורך אותו עקום הפונקציה החלקה הזו תיוצג כפונקציה ממשית במשתנה אחד. את הפונקציה הזו אפשר לגזור בצורה הרגילה וכך לראות איך היא משתנה לאורך אותו קו (גדלה, קטנה וכו').
באופן פורמלי: תהי עקומה חלקה. נגדיר את הווקטור המשיק ל- בנקודה (על ידי הפעולה שלו על פונקציה חלקה):
- .
זהו וקטור משיק (לפי ההגדרה הקודמת- כלומר פונקציונל ליניארי שמקיים את כלל לייבניץ). יתר על כן- כל וקטור משיק ניתן להצגה כמשיק של עקום חלק כלומר זו הגדרה שקולה להגדרה הקודמת של המרחב המשיק.
מבנים נוספים[עריכת קוד מקור | עריכה]
האגד המשיק[עריכת קוד מקור | עריכה]
האגד המשיק הוא איחוד כל המרחבים המשיקים על פני כל היריעה, מסומן ב . איחוד זה הוא איחוד זר כיוון שכל וקטור משיק שייך למרחב משיק של נקודה אחת בלבד, מעצם ההגדרה שלו (בעצם כל וקטור הוא מהצורה כאשר ).
על האגד המשיק קיים מבנה טבעי של יריעה שנוצר על ידי המפות: כאשר n הקוארדינטות הראשונות פועלות על p ו-n האחרונות על v, ו- היא מפה שמכילה את p. האגד המשיק הוא יריעה חלקה בממד כפול מממד היריעה.
פונקציות מהיריעה לאגד המשיק נקראות שדות וקטורים. כאשר הפונקציות האלו חלקות אומרים שזהו שדה וקטורי חלק (או ) בדרך כלל מתעסקים בשדות וקטוריים חלקים בלבד וכאשר אומרים "שדה וקטורי" הכוונה היא לשדה וקטורי חלק אלא אם אומרים במפורש אחרת. לשדות הווקטוריים יש חשיבות בהכללת אלמנטים מהמרחב המשיק שבכל נקודה לאגד המשיק כולו בצורה חלקה, כמו במטריקת רימן ובמערכת משוואות דיפרנציאליות על יריעות.
אם מערכת קואורדיטות מקומיות, אז ב-U ניתן להציג את השדה הווקטורי V על ידי:
- כאשר הפונקציות חלקות אם ורק אם V הוא שדה וקטורי חלק.
מההצגה הזו ניתן לראות את השדות הווקטוריים כאופרטורים על הפונקציות החלקות שמהווים הרחבה של הווקטורים המשיקים הנקודתיים ליריעה כולה. (כאשר אם g היא הפונקציה אז נגדיר ומההצגה של השדה הווקטורי כסכום- g חלקה.)
האגד המשיק הוא מקרה פרטי של אגד וקטורי מעל היריעה.
המרחב הקו-משיק[עריכת קוד מקור | עריכה]
המרחב המשיק הוא מרחב וקטורי מממד סופי, ולכן המרחב הדואלי שלו הוא גם כן מרחב וקטורי מאותו ממד. מרחב זה נקרא המרחב הקו-משיק ומסומן Tp*M. באמצעות מרחב זה מגדירים את מושג האינטגרל על היריעה.
עבור כל פונקציה חלקה f הדיפרנציאל של f, שמסומן df, הוא וקטור במרחב הקו-משיק שמוגדר על ידי הפעולה שלו על הווקטורים המשיקים:
- לכל
הבסיס הדואלי לבסיס הוא ולפי הנוסחאות של מרחבים דואליים מממד סופי:
קל לראות שכל וקטור קו-משיק ניתן להצגה כדיפרניציאל של פונקציה חלקה, ומכאן נובעת הגדרה שקולה למרחב הקו-משיק, על ידי פיתוח טיילור:
נגדיר אידיאל בחוג (חוג הפונקציות החלקות בסביבת הנקודה p) על ידי:
זהו האידיאל של כל הפונקציות החלקות שמתאפסות ב-p. מתוכו ניקח אידיאל קטן יותר - - שהוא האידיאל שנוצר על ידי כל הפונקציות שמתאפסות פעמיים כלומר כל הפונקציות שהן מכפלה של שתי פונקציות מ-. פונקציות אלו מאפסות כל וקטור משיק.
ביריעה חלקה ניתן להציג כל פונקציה חלקה על ידי טור טיילור המתאים לה, לדוגמה עבור יריעה מממד 2:
כאשר .
למעשה, בנוסחה למעלה הקואורדינטות x ו-y הן קואורדינטות מקומיות ולכן ההצבה שלהם בתוך הפונקציה f היא סימון מקוצר; f מקבלת ערכים מתוך היריעה עצמה ולא מהמישור האוקלידי, והכוונה היא לנקודה על היריעה שהקואורדינטות המקומיות שלה הן x,y.
חוג המנה איזומורפי באופן טבעי למרחב הקו-משיק, על ידי ההגדרה: כאשר היא פונקציית האיזומורפיזם בין למרחב הקו-משיק. בדרך זו גם ניתן להראות שממד המרחב המשיק הוא כממד היריעה.
דיפרנציאל של העתקה בין יריעות[עריכת קוד מקור | עריכה]
כל העתקה חלקה (דיפרנציאבלית) φ : M → N בין יריעות חלקות (דיפרנציאביליות) משרה מפה ליניארית בין המרחבים המשיקים
- .
אם המרחב המשיק מוגדר על ידי עקומות, מפה זו מוגדרת
- .
אם המרחב המשיק מוגדר על ידי דריבציות, אז
- .
ההעתקה הליניארית dφx נקראת לעיתים קרובות "דיפרנציאל" אך גם "נגזרת" או "total derivative" או ה"pushforward" של φ בנקודה x, ומסומנת במספר סימונים שונים, בהם
- .
במובן מסוים, הדיפרנציאל הוא הקירוב הליניארי הטוב ביותר ל-φ ליד x. כאשר , המפה dφx : TxM→R היא הדיפרנציאל הרגיל של φ במובן של חשבון אינפיניטסימלי. בקואורדינטות מקומיות הנגזרת של ƒ נתונה על ידי מטריצת יעקבי.
תוצאה חשובה לגבי הדיפרנציאל היא המשפט הבא:
- משפט. אם φ : M → N היא דיפאומורפיזם מקומי בנקודה x ב-M, אזי dφx : TxM → Tφ(x)N היא איזומורפיזם ליניארי. בכיוון ההפוך, אם dφx היא איזומורפיזם אזי קיימת סביבה פתוחה U של x כך ש-φ מעתיקה את U בצורה דיפאומורפית על תמונתה.
משפט זה הוא הכללה של משפט הפונקציה ההפוכה לפונקציות שהן העתקות בין יריעות.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- המרחב המשיק, באתר MathWorld (באנגלית)















































![{\displaystyle \mathrm {d} \varphi _{x}(X)=[\![f\mapsto X(f\circ \varphi )]\!]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4e66a0bcef23d37b697714919838b4f130617a9)

