חשבונייה

חשבונייה היא כלי חישוב המורכב ממסגרת ובה צירים, עליהם מחליקים חרוזים. חשבונייה יכולה לשמש כעזר מנייה, ובשימוש מתוחכם יותר לביצוע ארבע פעולות החשבון ופעולות חישוב מורכבות יותר. חשבוניות ידועות מהתקופה הקדומה, והיו בשימוש בבבל, סין ותרבויות נוספות במזרח, ביוון ורומא העתיקה, ועם הזמן, בעולם כולו. גם כיום משתמשים בחשבונייה מפעילים מיומנים שמוצאים אותה נוחה יותר מכלי חישוב מודרני כמו מחשבון, בעיקר במזרח. חישוב בעזרת חשבונייה נלמד בבתי ספר במקומות שונים בעולם. ביפן, קוריאה, ואולי במקומות נוספים נערכות תחרויות חישוב בעזרת חשבונייה, והמתחרים מבצעים פעולות מורכבות כמו חילוק וכפל במהירות דומה לחישוב במחשבון.
תיאור[עריכת קוד מקור | עריכה]
מסגרת החשבונית עשויה לרוב מעץ או פלסטיק ובעבר גם ממתכת; הצירים הם בדרך כלל מוטות אופקיים לאורכם מוזחים החרוזים, אך קיימות שיטות נוספות, כמו למשל הסורובן היפני, בו הצירים אנכיים.
בחשבונייה פשוטה, מושחלים על כל ציר תשעה חרוזים. כשכל החרוזים בצד אחד, הציר מייצג אפס. הזחת חרוז אחד לצד השני היא 1, וכשכל החרוזים בצד השני, הספרה היא 9.
כדי לחבר שני מספרים, "רושמים" את הראשון על החשבונייה, על ידי "כתיבת" כל ספרה לציר, לפי הסדר, ומוסיפים את השני על ידי הזחת חרוזים במספר הנדרש לכל ספרה. כשצריך להוסיף 1 לציר עליו כבר יש 9, מחזירים את כל החרוזים לצד שני, ומוסיפים 1 לציר הבא.
בחשבוניות מורכבות יותר יש שני צירים עבור כל ספרה, כאשר החרוזים על אחד מהם מייצגים 1, והחרוזים על השני מייצגים מספר גדול יותר, בדרך כלל 5. באופן זה, הסורובן היפני משתמש בחמישה חרוזים בלבד לזוג הצירים: בציר האחדות ארבעה חרוזים, ובציר החמישיות חרוז בודד.
היסטוריה של החשבונייה[עריכת קוד מקור | עריכה]
מקורה של החשבונייה לוט בערפל, כיוון שבמקומות ובעמים רבים עשו שימוש בחשבוניות. ידוע כי החשבונייה שימשה בתרבויות בבל וסין, והומצאה בזמן כלשהו בין שנת 2400 לפנה"ס לשנת 300 לפנה"ס. העדות המוקדמת ביותר המצויה בידינו לשימוש בחשבונייה מבוססת על "לוח סלמיס" מיוון העתיקה, המתוארך לסביבות שנת 300 לפנה"ס.
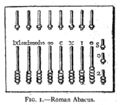
החשבונייה היוונית הייתה מבוססת על מניה בשיטה האקרופונית, והחשבוניות הרומיות שעוצבו בעקבות היווניות השתמשו בשיטה דומה.
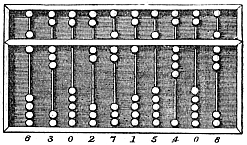
החשבונייה המוכרת לנו היום, בה ישנם שני חרוזים בחלק העליון וחמישה בתחתון, התבססה על דגם סיני מן המאה ה-12 בשם שואן פן. דגם זה נותר בעינו עד אמצע המאה ה-19, אז החל שימוש בשיטה בה יש רק חרוז אחד בחלק העליון. היפנים, שייבאו את החשבונית הסינית דרך קוריאה, אימצו שיטה משוכללת יותר שבה חרוז אחד בחלק העליון וארבעה בתחתון בתחילת המאה ה-17.
השימוש בחשבונייה כשיטה לחישוב נדחק במערב מפני חישוב במספרים, והחשבוניות המשיכו לשמש באסיה, שימוש הנמשך במקומות מסוימים עד היום, ונלמד בבתי הספר.
-
שיחזור של חשבונייה רומית עשויה ברונזה
-
שרטוט של חשבונייה רומית
-
חשבונייה עתיקה שנמצאה ביוון
סורובן[עריכת קוד מקור | עריכה]

חשבוניות עדיין נמצאות בשימוש, בעיקר באסיה. ביפן מיומנות בשימוש בחשבונייה נלמדת בבית ספר יסודי כחלק מתוכנית הלימוד, ומשרד המסחר מקיים בחינות בשימוש בחשבונייה, ומעניק תעודות לפי רמת המיומנות של הנבחן, בין רמה 5 (מפעיל מיומן) ורמה 1 (מסטר). מפעילי חשבונייה מומחים הם בדרך כלל, כמעט אוטומטית, מומחים גם בחישוב בעל-פה. בבית הספר מלמדים לדמיין בעיני רוחם חשבוניות כעזר לחישוב בעל פה.
כמצוין למעלה, בחשבונייה היפנית, שנקראת "סורובן", כל טור מחולק לשניים: בחלק העליון חרוז בודד, המציין 5, ובחלק התחתון ארבעה חרוזים. מצב ה"אפס" של חרוז ה-5 הוא למעלה, ומצב האפס של ארבעת החרוזים הוא למטה: כך, אם כל החרוזים מרוחקים מהמחיצה האופקית, העמודה מציינת "אפס", וכשכולם צמודים אליה, העמודה מציינת "9".
| הספרות 9 – 0 בסורובן | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
שיטת ספירה זו מכונה "דו-חמשית" או בי-קווינרי, היא עידון של שיטת הספירה העשרונית, בה ה"אטומים" הן הספרות. בשיטה הדו-חמשית, הספרה עצמה מחולקת לשני חלקים, חלק אחד שיכול לקבל את הערכים אפס עד ארבע, וחלק שני שיכול להיות אפס או חמש. כך למשל "3" יהיה "שלוש/אפס", ו-"7" יהיה "שתיים/חמש". חלוקה זו מפשטת את פעולת החיבור, והופכת אותה לפעולה טכנית שמפעיל מיומן מסוגל לבצע במהירות שלא ניתנת להשגה בחשבונייה מערבית, עם תשעה או עשרה חרוזים בעמודה[1]
שימוש[עריכת קוד מקור | עריכה]
יש טכניקות רבות לשימוש בחשבונייה, שמאפשרות ביצוע חישובים מורכבים. צורת השימוש המתוארת אינה בהכרח היחידה או הטובה ביותר לביצוע הפעולות.
חיבור[עריכת קוד מקור | עריכה]
פעולת החיבור היא הפעולה הבסיסית של החשבוניה: כמתואר למעלה, החיבור מתבצע על ידי "כתיבת" המחובר הראשון לחשבוניה, על ידי הזחת החרוזים, והמשך הזחת חרוזים, לפי ספרות המחובר השני, והעברת הנשא במעבר מ-9 ל-0.
חיסור[עריכת קוד מקור | עריכה]
בחיסור, רושמים את המחוסר לחשבונייה, וממשיכים בהזחת החרוזים בכיוון ההפוך עבור ספרות המחוסר השני. כאשר במוט רשום "0" ויש לחסר עוד אחד, מחזירים את החרוזים למצב "9", ו"שואלים" אחד מהמוט הבא, בדומה לאופן בו מעבירים את הנשא בחיבור.
כפל[עריכת קוד מקור | עריכה]
כפל מבוצע על ידי חזרה על חיבור: כדי לכפול ב-3, רושמים את הנכפל לחשבונייה, ואז מחברים אותו פעמיים נוספות. כדי לכפול ב-13, מחברים אותו לעצמו שלוש פעמים, ופעם נוספת, ב"הסטה" של אחד, כלומר את ספרת האחדות שלו מחברים לציר שמייצג את ספרת העשרות בחשבונייה, וכן הלאה.
המשמעות היא שכדי לבצע כפל יש לבצע מספר פעולות חיבור, אך מספרן אינו הכופל, אלא סכום הספרות של הכופל: כדי לכפול ב-1306, יש צורך לבצע עשר פעולות חיבור, ולא אלף.
יש טכניקות רבות לקיצור והקלת הפעולה: למשל, כדי לכפול ב-19, ניתן לבצע עשר פעולות חיבור. אפשר, במקום זאת, לבצע שתי פעולות חיבור, ופעולת חיסור אחת: כופלים ב-20, כלומר מחברים את הנכפל פעמיים, בהסטה של ציר אחד, כלומר כפל ב-10, ואז מחסרים את הנכפל פעם אחת: עשרים פחות אחד הם 19.
כאשר נחוץ לכפול את אותו המספר במספרים שונים בזה אחר זה, ניתן לכפול אותו בספרות 1 עד 9, ולרשום את התוצאות. בעזרת הרשימה מתקצרות פעולות הכפל הבאות: מספר הפעולות הנחוץ הופך למספר הספרות, ולא סכום הספרות של הכופל בשיטה שתוארה למעלה.
חילוק[עריכת קוד מקור | עריכה]
חילוק בחשבונייה מתבצע על ידי הזנת המונה לחשבונייה, החל בספרה הגבוהה ביותר, על ידי השלמה באפסים של הספרות הנמוכות. מבצעים חיסור כאשר המכנה ב"הזחה" המרבית בה הוא עדיין קטן מהמונה. ממשיכים בחיסור עד שהמכנה גדול יותר מהמספר שרשום בחשבונייה. מספר פעולות החיבור שבוצעו בהצלחה הוא ערך הספרה. ממשיכים לחסר את המכנה בהזחה קטנה יותר, עד ששוב הוא גדול מהמספר שרשום בחשבונייה, ומספר הפעולות שבוצעו בהצלחה הוא הספרה הבאה. ממשיכים כך עד ש"נגמרות ההזחות", כלומר ספרת האחדות של המכנה היא אותה ספרה כמו ספרת האחדות של המונה. ניתן לסיים את החילוק בנקודה זו, כאשר המנה היא המספר שנצבר במשך הפעולה, והשארית היא המספר שרשום בחשבונייה. אם השארית אינה אפס, ניתן להמשיך את הפעולה על ידי סימון נקודה עשרונית בתוצאה, והמשכת הפעולה כאשר המכנה מוזח מימין לנקודה. דיוק הפעולה תלוי רק במספר הצירים שיש בחשבונייה: בחשבונייה עם שמונים צירים, אפשר לקבל בפעולת חילוק עד שמונים ספרות, או ליתר דיוק, שמונים פחות מספר הספרות של המכנה.
כמו בכפל, גם לחילוק יש שיטות משוכללות יותר, שמאפשרות למפעיל מיומן לבצעו במהירות רבה בהרבה מהשיטה הפשטנית שתוארה.
אטימולוגיה[עריכת קוד מקור | עריכה]
מקור המונח הלועזי Abacus ("אבקוס") כשם לחשבונייה, מקורו במילה היוונית άβακας ("אבקס", לוח חישוב). למונח יש גם פירוש נוסף, "לוח שעליו אבק או חול" לצורך שרטוט גאומטרי ואריתמטי, ישנם בלשנים המשערים כי המילה היוונית מבוססת על השורש השמי "א-ב-ק" המצוי במילה העברית והפיניקית "אבק", שמשמעותה חול.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
 ביל יאנה, חשבונייה: 3000 לפנה"ס, באתר הספרייה הווירטואלית של מטח, מתוך הספר "100 המצאות ששינו את העולם"
ביל יאנה, חשבונייה: 3000 לפנה"ס, באתר הספרייה הווירטואלית של מטח, מתוך הספר "100 המצאות ששינו את העולם"- מדריך לביצוע ארבע פעולות חשבון, שורש ריבועי ומעוקב בעזרת חשבונייה (באנגלית)
- חשבונייה, באתר MathWorld (באנגלית)
- חשבונייה, באתר אנציקלופדיה בריטניקה (באנגלית)
 אבקוס, דף שער בספרייה הלאומית
אבקוס, דף שער בספרייה הלאומית