מכונת חישוב


מכונת חישוב היא מכונה המיועדת לעזור בעריכת חישובים, בעזרת מערכות מכניות, המבוססות על מנגנונים כמו מנופים, גלגלי שיניים, תמסורות, וכדומה או מערכות אלקטרוניות. בצורתה הבסיסית מכונת חישוב מסוגלת לבצע את ארבע פעולות החשבון, ובגרסאות מתקדמות יותר, אלקטרוניות, ניתן לבצע פעולות נוספות, כגון העלאה בחזקה, הוצאת שורש ריבועי ופונקציות טריגונומטריות.
סקירה[עריכת קוד מקור | עריכה]
תרבויות שונות, למן העת העתיקה, המציאו והשתמשו בעזרים שונים לביצוע פעולות חשבון. העזרים הראשונים יועדו לעזר בספירה, כמו מקל ספירה, שדוגמאות שלו ידועות בארכאולוגיה עוד בתקופה פרהיסטורית. ידוע גם השימוש בערימת אבנים כעזר לספירה, שמוזכר במקורות היסטוריים שונים, למשל אצל דמוסתנס.
המתקן המכני הראשון שיועד לסייע בביצוע פעולות חשבון, מעבר לספירה, הוא כנראה החשבונייה ("אבאקוס"). עדויות ראשונות לחשבוניות הופיעו בשומר, בין המאות ה-27 ל-23 לפני הספירה. חשבוניות אלו מבוססות על בסיס ספירה 60, הנקרא בסיס סקסגסימלי, בו השתמשו השומרים. מאוחר יותר יש עדויות לחשבוניות בתרבויות נוספות – במצרים העתיקה, וממלכת פרס, ומשם בתרבויות הסמוכות, הודו, יוון ועוד. החשבונייה בצורתה המוכרת הופיעה לראשונה בסין הקדומה במאה ה-2 לפני הספירה, ובשינויים מועטים. בסין משתמשים בחשבוניות כאלו עד היום.
מתקנים מכניים שונים לביצוע חישובים המשיכו להופיע בעת העתיקה:
- מנגנון אנטיקיתרה, שפרטי פעולתו לא ידועים במדויק, וככל הנראה שימש לחישוב תנועת גרמי שמיים, וכנראה אפשר לחזות ליקוי חמה וליקוי ירח, מבוסס על גלגלי שיניים, וכנראה הכיל מחוונים שהציגו את תוצאת החישוב. המנגנון, או מנגנון דומה לו, מוזכר על ידי כותבים מהתקופה, אבל התיאורים לא ברורים ומפורטים מספיק כדי להבין את תפקידו המדויק, מה גם שהמידע שהיה בידי הכותבים הללו לגבי המתקן חלקי, ואולי שגוי.
- המהנדס הרומי ויטרוביוס, בנה מתקן למדידת מרחקים (אודומטר או מד מרחק), שהשתמש במערכת תמסורת כדי להתמיר מספר סיבובים של אופן מרכבה לסיבוב אחד של גלגל, שבסיבובו הפיל אבן ממצבור אבנים לסל. כיוון שהיקף גלגל המרכבה ויחס התמסורת ידועים, כל אבן מייצגת מרחק קבוע ידוע. בעזרת ספירת האבנים, ניתן לחשב את המרחק.
בתחילת המאה ה-17 המציא המתמטיקאי הסקוטי ג'ון נפייר עזר חישוב מכני שמוכר כעצמות נפייר. עצמות נפייר מסייעות בביצוע פעולת כפל, ובעזרתן ניתן לבצע כפל כשהמשתמש נדרש לבצע פעולות חיבור בלבד (אין לבלבל עזר חישוב זה עם לוגריתמים, שגם הם הומצאו על ידי נפייר, וגם בעזרתם ניתן לחשב מכפלות בעזרת פעולות חיבור בלבד).
מאוחר יותר, במאה ה-17, החלו להופיע מכונות חישוב מכניות שמבוססות על מערכיות גלגלי שיניים ותמסורות. שימוש במכונות חישוב כאלו החל להתפשט מאמצע המאה ה-19, במהפכה התעשייתית, ולקראת סוף המאה ה-19 כבר התקיימה תעשייה, שעדיין הייתה צעירה אך כבר הכילה עשרות אם לא מאות יצרנים שונים, בכתריסר ארצות שונות.
בתקופה זו הופיע בבירור הופיעה בבירור הפרדה בין שני "זנים" של מכונות חישוב: הזן הראשון מכונה "מכונות חיבור", אף כי בחלקן ניתן לבצע גם פעולת חיסור, והזן השני נקרא "מכונות ארבע פעולות", בעזרתן ניתן לבצע חיבור, חיסור, חילוק וכפל.
במאה ה-20 התעשייה התפתחה במהירות, תפוצת המכונות המשיכה להתרחב, לשימושים מגוונים יותר ויותר – מכונות החיבור מצאו את מקומן במשרדי ניהול חשבונות ובקופות רושמות, ומכונות ארבע פעולות, בשימוש מדענים, מהנדסים, בנקאים, מודדים, ומקצועות רבים נוספים בהם נחוץ לבצע חישובים.
יחסית למחשבונים בני ימינו, מכונות החישוב גדולות, כבדות, ויקרות, ומעולם לא הגיעו לתפוצה דומה לתפוצת המחשבונים. עד תום עידן מכונות החישוב הופיעו שכלולים רבים, כמו הנעה חשמלית, הדפסה, ואוטומציה מקיפה יותר ויותר, וגם ממשק המשתמש המשיך להשתכלל – באריתמומטר המקורי ביצוע פעולת כפל היא פעולה מורכבת הדורשת מיומנות, כשבמכונות החישוב האחרונות, אופן השימוש דומה לשימוש במחשבון בן ימינו, כשגם החילוק וגם הכפל מחושבים באופן אוטומטי לחלוטין. אחד היצרנים האמריקאיים (פרידן), בנה מכונות שיכלו אפילו לחשב שורש ריבועי.
ב-1962 הופיעה באנגליה מכונת החישוב האלקטרונית הראשונה, ובין השנים 1962 ו-1970, התקיימו מכונות החישוב המכניות והאלקטרוניות אלו לצד אלו. מכונות החישוב האלקטרוניות הראשונות השתמשו בממשק משתמש זהה למכונות החישוב המכניות, אך תוך זמן קצר ממשק המשתמש המוכר, של עשרה מקשי ספרות, עם מקשים נוספים להזנת סדר הפעולות לחישוב. רבות ממכונות החישוב האלקטרוניות היו ניתנות ל"תכנות", שביצעו תוכניות חישוב קצרות של כמה עשרות פעולות, כדי לחשב תוצאות מורכבות. באמצע העשור כבר היו מכונות חישוב אלקטרוניות "מדעיות", עם יכולות נוספות, כמו חישוב פונקציות "מדעיות" של לוגריתמים והעלאה בחזקה. ב-1968 מכונת חישוב של HP, בשם 9100, הציגה פונקציות מדעיות מלאות למחשבון – לוגריתמים, שימוש ב"נקודה צפה", עם תחום בין ל- ועוד.
עידן מכונות החישוב המכניות הסתיים בצורה פתאומית, כאשר המחשבונים האלקטרוניים, שמראשיתם עלו על המכונות המכניות במהירותן ובפעולתן השקטה, הכו את מכונות החישוב גם במחיר, בעקבות פיתוח המעגל המשולב. אחרי שיאי מכירות לקראת סוף שנות ה-60 של המאה העשרים, עד אמצע שנות ה-70 כבר לא נותר אף יצרן פעיל במערב. בגוש המזרחי נותרו מספר יצרנים פעילים של מכונות חישוב מכניות עד סוף שנות ה-70, כנראה משום שזמינותם הנרחבת של המחשבונים הופיעה במדינות אלו מאוחר יותר.
| מספרי מכונות חישוב מכניות ומחשבונים שנמכרו ביפן, בין השנים 1960 ו-1975 | ||||
|---|---|---|---|---|
| "טייגר" היה היצרן הגדול ביותר של מכונות חישוב ביפן, לצד מספר מתחרים[1]. | ||||
| שנה | טייגר ידני | טייגר חשמלי | כל היצרנים, יפנים ואחרים | מכונות חישוב אלקטרוניות ומחשבונים |
| 1960 | 19683 | 37968 | ||
| 1961 | 22130 | 560 | 46030 | |
| 1962 | 28160 | 400 | 51168 | |
| 1963 | 27040 | 48255 | ||
| 1964 | 30980 | 200 | 54616 | |
| 1965 | 30400 | 400 | 53259 | 4,355 |
| 1966 | 27935 | 300 | 53671 | 25,479 |
| 1967 | 31800 | 170 | 68703 | 63,137 |
| 1968 | 38200 | 85084 | 163,387 | |
| 1969 | 22770 | 75554 | 453,964 | |
| 1970 | 18410 | 38415 | 1,423,487 | |
| 1971 | 9220 | 20802 | 2,040,287 | |
| 1972 | 290 | 6793 | 3,886,221 | |
| 1973 | 770 | 5177 | 9,960,403 | |
| 1974 | 380 | 276 | 15,452,709 | |
| 1975 | 160 | 30,040,140 | ||
מכונות מוקדמות - המאה ה-17[עריכת קוד מקור | עריכה]
שיקארד[עריכת קוד מקור | עריכה]
מכונת החישוב הידועה הראשונה נבנתה על ידי וילהלם שיקארד, כנראה ב-1623. המכונה של שיקארד לא שרדה, ולא ברור כמה מכונות נבנו – כנראה שתיים או שלוש. רוב מה שידוע על המכונה הזו, מגיע ממכתבים שכתב שיקארד לידידו, האסטרונום והמתמטיקאי יוהאנס קפלר. שיקארד כתב לקפלר שהוא הזמין אצל שען עותק של המכונה שמיועד לקפלר עצמו, אך שרפה בבית המלאכה גרמה לאבדן המכונה שיועדה לקפלר. המידע והשרטוטים במכתבים אלו אינו מספיק במלואו כדי לבנות דגם עובד של המכונה. ניסיונות לבנות דגם של המכונה לפי הרישומים הקיימים, הצריך הוספת מספר מנגנונים וגלגלי שיניים שלא מופיעים בתרשים. דגמים אלו חושפים חולשה במנגנון הנשא במכונה, וכנראה, מפעיל המכונה היה צריך "לעזור" לגלגלי השיניים בחישובים מסוימים.
למכונה שני חלקים נבדלים: חלקה העליון הכיל מנגנון מבוסס על עצמות נפייר, ובעזרתו ניתן למצוא את המחוברים שסכומם נותן את המכפלה. החלק התחתון הכיל מכונת חיבור, שבעזרתה ניתן לחשב את סכום המספרים באופן מכני.
בלייז פסקל וה"פסקלין"[עריכת קוד מקור | עריכה]
 ערך מורחב – פסקלין
ערך מורחב – פסקלין
מכונת החישוב פסקלין, הומצאה על ידי המתמטיקאי הצרפתי בלייז פסקל, ב-1642, כשהיה בן 19. הוא המציא את המכונה כדי לעזור לאביו, שהיה מפקח מס, ונזקק לחישובים רבים ומייגעים. מכונה זו יכלה לבצע חיבור וחיסור בלבד, אבל פתרה את האתגר של העברת הנשא מספרה לספרה הבאה באופן אמין יותר מאשר במכונתו של שיקארד. העברת הנשא בצורה אמינה המשיכה להיות אחד האתגרים שעמדו בפני מתכנני מכונות חישוב מכניות, וממציאים שונים פתרו אותו בדרכים שונות.
בפסקלין, הזנת המחובר מתבצעת על ידי סיבוב גלגלים, או חוגות, באמצעות חרט, בדומה לאופן בו מפעילים חוגת טלפון. סיבוב החוגות הוא שמפעיל את המכונה. ניתן לסכם בעזרת המכונה טורי מספרים, ותוצאת החישוב (או תוצאת הביניים, כשנמצאים באמצע טור המספרים) מופיעה בשורת חלוניות מעל שורת הגלגלים. פעולת חיסור בוצעה על ידי הוספת המספר המשלים, טכניקה שהמשיכה להיות בשימוש בחלק ממכונות החישוב של הדורות הבאים.
משום שהמכונה ביצעה חיבור וחיסור בלבד, ניתן היה ליצור דגמים שאינם מוגבלים לחשבון בשיטה עשרונית, ובחלק מהמכונות, שיועדו לצרכים ספציפיים, הספרות הנמוכות השתמשו בבסיסי ספירה אחרים, כדי לייצג חלוקות לא עשרוניות של מטבעות ומידות, שלא השתמשו בשיטה עשרונית (מאוחר יותר, במהפכה הצרפתית, השיטה המטרית ייתרה את הצורך בשיטות כאלו). כך, במכונות שיועדו לחשבונאות, הספרות התחתונות התחלקו ל-12 ו-20, כדי לייצג את חלוקת המטבע, ובמכונות שיועדו למודדים החלוקה הייתה ל-12, 12, ו-6 עבור רגל צרפתית, והמידות הבאות. בכל המכונות, הספרות העליונות השתמשו בשיטה עשרונית.
פסקל בנה כ-50 אבות טיפוס, עד שהגיע למכונה שהשביעה את רצונו, אותה הציג לציבור ב-1645. הוא המשיך לבנות ולמכור מכונות, וידוע על לפחות 20 מכונות שנבנו ונמכרו, מהן ידועות תשע מכונות קיימות היום, ומוצגות במוזאונים שונים.
גוטפריד לייבניץ[עריכת קוד מקור | עריכה]
 ערך מורחב – מחשב הפסיעות
ערך מורחב – מחשב הפסיעות
המתמטיקאי הגרמני גוטפריד לייבניץ ניסה לתכנן מכונת חישוב שהייתה מבוססת על הפסקלין, ותוכל לבצע גם כפל. ככל הנראה ללייבניץ לא הייתה גישה לפסקלין, והוא התבסס על תרשימים, שהובילו אותו להבנות מוטעות לגבי אופן פעולת המכונה. מאוחר יותר זנח לייבניץ את הניסיון הזה, ותכנן ובנה מכונה שפועלת על עקרונות אחרים. העקרונות הבסיסיים שמכונתו של לייבניץ מבוססת עליהם היו מוצקים ומוצלחים, ומכונות חישוב ב-200 השנים הבאות המשיכו להיבנות לפי עקרונות אלו, עד הקורטה שייצורה נמשך עד 1970. לייבניץ המשיך לפתח את המנגנון במשך 40 שנה. ידוע על שתי מכונות שנבנו עבור לייבניץ לפי התכנון הזה, אחת ב-1694, והשנייה בשנת 1706. לייבניץ גם תיאר, באחד התיאורים המוקדמים הידועים, את מנגנון גלגל הפינים. שני מנגנונים אלו, כלומר התוף המדורג וגלגל הפינים, שאת שניהם אפשר לייחס ללייבניץ, מהווים את המנגנון הבסיסי שמניע את רוב מכונות החישוב של ארבע פעולות שנבנו.
שלא כמו במכונתו של פסקל, במכונה של לייבניץ הזנת הקלט כשלעצמה לא מפעילה את המכונה, וההפעלה מתבצעת בנפרד, על ידי סיבוב ארכובה. הבדל זה מאפשר לחבר את הקלט יותר מפעם אחת, באמצעות סיבובים נוספים של הארכובה. היכולת לחזור על פעולת החיבור, בצירוף להמצאה נוספת, עגלה, המאפשרת להזיח את הקלט ביחס לתוצאה, מאפשרת למכונה לבצע כפל, בעזרת חיבור חוזר. אף על פי שהמכונה נבנתה לפי עקרונות שהמשיכו לשמש לבניית מכונות חישוב במשך כמעט 300 שנה, המכונות עצמן לא סיפקו תוצאות נכונות באופן אמין, ועברו כמעט מאה שנים עד שמכונה הבנויה לפי עקרונות אלו פעלה באופן אמין ומדויק.
אחרים[עריכת קוד מקור | עריכה]
ממציאים נוספים בנו מכונות חישוב במאה ה-17, ביניהם האיטלקי טיטו ליביו בוראטיני, האנגלי סמואל לורלנד, והצרפתי רנה גרילה (René Grillet de Roven) אך אף אחד מהם לא זכה להשפעה משמעותית.
-
איור של מכונת החישוב של שיקארד, ממכתב שכתב לידידו יוהאנס קפלר
-
רפליקה (משוערת) של מכונת החישוב של שיקארד. החלק העליון, הניצב, מכיל מערכת המבוססת על עצמות נפייר, והחלק התחתון הוא מכונת חיבור
-
ה"פסקלין" – מכונת החישוב של פסקל
-
רפליקה של מכונת החישוב של לייבניץ, במוזיאון הגרמני
המאה ה-18[עריכת קוד מקור | עריכה]
במאה ה-18 המשיכו ממציאים שונים בגרמניה, פולין, איטליה, צרפת ואנגליה לבנות ולפתח מכונות חישוב, בדרך כלל על בסיס המכונות של פסקל ולייבניץ. אף אחת מהן לא זכתה לתפוצה נרחבת, וחלקן נשארו בגדר תכנון בלבד, ואלו שנבנו, רובן ככולן נבנו כדגם יחיד, או אבטיפוס. רשימת הממציאים והבונים ארוכה, וקיימים עד היום דגמים מקוריים, חלקם עובדים, של מכונות חישוב מהתקופה, במוזאונים ובאוספים פרטיים שונים ברחבי העולם. הרב, הממציא והשען אברהם יעקב שטרן מפולין המציא מספר גרסאות של מכונות החישוב בשנות החמישים של המאה ה-18, ואף זכה למלגה מטעם השלטון הרוסי לשפר את המצאותיו. אחריו, הכומר והשען הגרמני האן Hahn בנה, החל מ-1774 מכונות חישוב. הוא ובני משפחתו ייצרו מספר לא ידוע של מכונות, מהן לא פחות מ-10 שרדו עד למאה ה-20, ולפחות שתיים מהן מוצגות היום במוזאונים שונים. לפי ארנסט מרטין[2], המכונה של האן נחשבת למכונת החישוב המוצלחת הראשונה.
בתקופה זו מכניקה עדינה הייתה נחלתם של שענים, ואכן, חלק ניכר ממכונות החישוב נבנו בידי שענים, והיו ידועות בכינוי "שעון חישוב" (Rechenuhr).
המאה ה-19[עריכת קוד מקור | עריכה]
במהלך המאה ה-19 מכונת החישוב הפכה למוצר. בתחילת המאה, ערב המהפכה התעשייתית, היו אמנם מכונות חישוב בעולם, אך כמעט כולן נבנו ידנית, כדגם יחיד או מספר קטן של יחידות. בסוף המאה הייתה תעשייה מבוססת של מכונות חישוב בארצות רבות, ביניהן צרפת, גרמניה, אנגליה, שוודיה, רוסיה, ארצות הברית, שווייצריה, איטליה, ועוד. עשרות יצרנים במדינות אלו ייצרו מכונות חישוב במאות דגמים. אמנם אין מידע מדויק על המספר הכולל של מכונות חישוב בסיום המאה, אבל מידע מכמה מהיצרנים הגדולים מורה בבירור שמדובר במאות אלפי יחידות, אולי אף יותר, במאות דגמים שונים, שנבנו ונמכרו.
שארל קסביה תומא דה קולמר, אריתמומטר[עריכת קוד מקור | עריכה]
 ערך מורחב – שארל קסביה תומא דה קולמר
ערך מורחב – שארל קסביה תומא דה קולמר
תומא, שמוכר בכינוי "תומא דה קולמר", כלומר תומא מהעיירה הצרפתית קולמר, הגיש ב-1820 בקשה לפטנט על מכונת חישוב של ארבע פעולות, שמבוססת על מכונת החישוב של לייבניץ. תומא קרא למכונה שלו אריתמומטר, ייצר ומכר מספר קטן של מכונות, וב-1844 תכנן מחדש את המכונה, ושוב ב-1850. התכנון החדש הסיר את אחת היכולות של המכונה ("כפל אוטומטי"), והוסיף במקומו פריט שנשאר סטנדרטי במכונות חישוב למשך שאר הזמן בו מכונות כאלו נבנו, בשם "מונה הסיבובים" (מכונה גם "אוגר המנה"). המכונה אמינה יותר, ומתאימה יותר לייצור תעשייתי. תומא החל לייצר ולמכור את המכונה שלו, בצורה תעשייתית, החל מ-1852, כשהייצור עצמו התבצע על ידי מכונאים שונים, והתיכון עצמו המשיך להתפתח לפחות עד שנות ה-60 של המאה, ובעשורים האחרונים הייצור עבר למכונאי בשם לואי פאיין. עם מותו של תומא ב-1870, פאיין המשיך לייצר את המכונה, ועם מותו שלו, אלמנתו המשיכה בייצור, עד לתחילת מלחמת העולם הראשונה. תומא עצמו ייצר מעל 1,000 מכונות, ופאיין אחריו ייצר עוד כמה אלפים. בשנות ה-70 של המאה ה-19 החלו יצרנים נוספים לייצר ברישיון "תואמים" לאריתמומטר, באנגליה ובגרמניה, ובמקביל החלו להופיע דגמים נוספים של מכונות חישוב. האריתמומטר, נחשב בדרך כלל למכונת החישוב המוצלחת הראשונה, ולמכונה שייסדה את תעשיית מכונות החישוב. במקרים רבים המושג "אריתמומטר" נחשב לשם כללי למכונת חישוב של ארבע פעולות. אפשר לראות במכונות חישוב מסוימות, אפילו מהדור האחרון של מכונות החישוב המכניות, כאבולוציה של מכונתו של תומא[3].
בולדווין ואודהנר[עריכת קוד מקור | עריכה]
בין 1873 ו-1875, הגישו פרנק בולדווין (אנ') בארצות הברית, ווילגודט אודהנר (אנ') ברוסיה, בקשות לפטנטים, ושניהם קיבלו מספר פטנטים למנגנון חדש למכונת חישוב. שני הפטנטים מתארים מתקן דומה, שמוכר לפעמים כ"אודהנר", "בולדווין", או "גלגל פינים". אודהנר החל לייצר ולמכור מכונות חישוב המבוססות על הפטנט בסנקט פטרבורג ברוסיה, בשם "אריתמומטר".
בשנים הבאות חברות שונות, בפרט בגרמניה ואנגליה רכשו זכויות ייצור לפי הפטנט של אודהנר. אחת מהן, ברונשוויגה מבראונשווייג, הייתה לאחת ממכונות החישוב הידניות הנפוצות והידועות ביותר.
המפעל של אודהנר ברוסיה הולאם אחרי מהפכת אוקטובר, והמשיך לייצר מכונות חישוב זהות כמעט למכונה של אודהנר, בשם "פליקס", עד לשנות ה-70 של המאה.
בולדווין המשיך להמציא ולחדש בתחום מכונות החישוב, ולזכותו נזקף, בין השאר, גם התכנון המוצלח הראשון של מכונות ארבע פעולות עם לוח מקשים.
רוב מכונות החישוב המכניות מבוססות, בצורה זו או אחרת על אחד משני המנגנונים הללו, או על וריאציה שלהם: התוף המדורג של לייבניץ, או גלגל הפינים של אודהנר ובולדווין.
מעניין לציין שהרעיון של גלגל פינים היה ידוע כבר ללייבניץ, והוא תיאר מכונה שמבוססת עליו, אם כי לא ידוע על ניסיון שלו לבנות מכונה כזו בפועל. כמה מהמכונות המוקדמות יותר מהמאה ה-18 וה-19, היו מבוססות על צורות שונות של גלגל פינים, אבל המנגנון של אודהנר/בולדווין הוא המימוש המוצלח הראשון, ועד תום עידן מכונות החישוב יוצרו מכונות מבוססות על המנגנון הזה.

מנועי הפרשים[עריכת קוד מקור | עריכה]
 ערכים מורחבים – צ'ארלס בבג', מנוע הפרשים
ערכים מורחבים – צ'ארלס בבג', מנוע הפרשים
"מנוע הפרשים" הוא סוג מיוחד של מכונת חישוב מורכבת, בה פועלות במקביל מספר פעולות חיבור.
תפקיד המכונה הוא חישוב ערכו של פולינום בסדרת נקודות עוקבות. החישוב מתבצע בעזרת אלגוריתם המבוסס על "סדרת הפרשים", ודורש פעולות חיבור בלבד.
התועלת בערכי הפולינום בסדרת נקודות עוקבות נובע מהעובדה שפונקציות אנליטיות ניתנות לקירוב ברמת דיוק גבוהה על ידי פולינום. לוגריתם, פונקציות טריגונומטריות הן פונקציות אנליטיות, ומנוע ההפרשים מנוצל כדי לבנות לוחות של פונקציות אלו. לוחות אלו משמשים בחישובים שונים, ובפרט בניווט. בזכות האלגוריתם, כלומר היתכנות, והשימושיות, נעשו ניסיונות, חלקם מוצלחים, לבנות מנועי הפרשים, למטרת ייצור אוטומטי של לוחות.
במהלך המאה ה-19 תוכננו מספר מנועי הפרשים, הידוע מהם על ידי בבג'.
בבג' עצמו מעולם לא השלים בניית מנוע הפרשים, אך אחרים תכננו ובנו מנועי הפרשים מעט פחות ידועים, שפעלו בהצלחה ואף שימשו להדפסת לוחות. הראשון בהם היה השוודי פר גאורג שוץ (אנ'), ובנו שהמשיך אחריו. שוודי אחר, בשם מרטין ויברג, בנה מכונה בהשראת מכונתו של שוץ, והשתמש בה להדפסת לוח לוגריתמים. למידע נוסף ראו בערך המורחב.
מכונת חישוב טרנארית[עריכת קוד מקור | עריכה]
ב-1840, בנה תומאס פאולר (אנ') מכונת חישוב המבוססת על ייצוג המספרים בבסיס 3 מאוזן (וריאציה על בסיס ספירה 3, בה משתמשים בספרות מינוס 1, 0, ו-1 במקום 0, 1, ו-2 (Balanced ternary)). פאולר המציא לפני כן את שיטת החימום המרכזי בעזרת סירקולציה של מים חמים, וחש שהמצאתו נגזלה ממנו עקב מגבלות בחוקי הפטנטים. כנראה מסיבה זו הוא פיתח את מכונת החישוב שלו לבדו, ובנה דגם של המכונה בסדנה בביתו. הדגם שבנה פאולר לא שרד, אם כי ידועים עליו מעט פרטים: פאולר בנה את הדגם מעץ, והמכונה הייתה גדולה: אורכה היה כשני מטרים, רוחבה כמטר, וגובהה כ-30 סנטימטר. פאולר הדגים את המכונה למספר אנשים, בהם צ'ארלס בבג' ואוגוסטוס דה מורגן. זה האחרון השאיר תיאור בן שני דפים של המכונה, ולפי תיאור זה נבנה במאה ה-21 דגם של המכונה[4].
קומפטומטר[עריכת קוד מקור | עריכה]
 ערך מורחב – קומפטומטר
ערך מורחב – קומפטומטר
ב-1884, בנה הממציא דור פלט (אנ') בארצות הברית אבטיפוס למכונה, שנקראה אחר כך "קומפטומטר". מבחינה מסוימת הקומפטומטר הוא מכונת חישוב פשוטה, המיועדת לחיבור וחיסור בלבד. החידוש בקומפטומטר הוא אופן ההפעלה: לקומפטומטר לוח מקשים מלא (ראו תמונה בגלריה), כלומר עבור כל ספרה, 9 מקשים מ-1 עד 9 (אין צורך במקש עבור 0): תשעה מקשים ליחידות, תשעה למאות, תשעה לאלפים וכן הלאה. "לוח מקשים מלא" הפך לסימן ההיכר של מכונות החישוב המתקדמות (ולכן גם היקרות) ביותר, ונשאר כך כמעט עד תום עידן מכונות החישוב. דור חבר עם איש העסקים רוברט טרנט (Robert Tarrant), ויחדיו הם הקימו את חברת "פלט וטרנט" לייצור מכונות חישוב. החברה שינתה שמה מאוחר יותר ל"קומפטומטר", והמשיכה לייצר מכונות חישוב עד המחצית השנייה של המאה ה-20.
אחד הדברים שייחדו את הקומפטומטר, ובמידה מסוימת עשו אות מורה הדרך ונותן כיוון לתעשייה כולה, הוא הדגש על נוחות, מהירות, דיוק ההפעלה, ומניעת טעויות מפעיל. המכונות מכילות מנגנונים רבים שתפקידם למנוע, או לפחות למזער טעויות אפשריות בהפעלה, כמו לחיצה חלקית על מקש, לחיצה על שני מקשים באותו טור מספרים, וטעויות רבות נוספות.
חברת פלט וטרנט פתחה רשת בתי ספר להכשרת מפעילי קומפטומטר, שהמשיכו לפעול עד שנות ה-50 וה-60 של המאה ה-20. בשנות ה-20 של המאה העשרים היו מעל 150 בתי ספר כאלו – מעל מאה מהם בארצות הברית, וכחמישים בשאר העולם[5]. בתי ספר אלו הכשירו מאות אלפי "מחשבים" (computers. כיום נהוג לכנות את המקצוע שעבר מהעולם "מחשב אנושי" (Human Computer) ), כלומר אנשים (רובם נשים) שמקצועם הוא ביצוע חישובים. משרדי ממשלה, חברות מסחר גדולות, בנקים, חברות ביטוח ומוסדות דומים, הפעילו "חדרי חישוב", בהם ישבו טורי מפעילים, לפעמים עשרות, כשכל אחד ואחת מהם מסכמים טורי מספרים בעזרת קומפטומטר, לצד מנהלי חשבונות שהשתמשו גם במכונות חישוב מסוגים נוספים.
באופן עקרוני, המכונה היא מטיפוס "פסקלין", והפעולה היחידה שהיא מבצעת היא חיבור (חיסור מתבצע כל ידי "חיבור המשלים"), אך בעזרת השימוש בלוח המקשים, אימנו בתי הספר את המפעילים לבצע גם פעולות נוספות, כמו כפל וחילוק. לעומת "הדפסה עיוורת" במכונת כתיבה, שימוש באצבעות שתי הידיים מאפשר להזין מספרים בהקשה בו־זמנית על מספר מקשים שכל אחד בטור אחר, ולקצב הזנת הנתונים של מפעיל קומפטומטר מיומן אין תחרות, גם במקלדות מודרניות.
"מפעיל קומפטומטר", ואפילו "מפעיל קומפטומטר מדופלם" היו למושגים מוכרים. לפי ארנסט, מפעיל קומפטומטר מיומן מבצע בין 50,000 ל-200,000 הקשות מקש ביום.
ב-1958 רכשה חברת Bell Punch האנגלית את הזכויות לשימוש בשם ובתיכון הקומפטומטר (זמן קצר לאחר מכן הציגה אותה חברה את מכונת החישוב האלקטרונית הראשונה – ANITA). החברה המשיכה לייצר, ואף לפתח את הקומפטומטר באנגליה, ומכרה אותו בשם זה מספר שנים נוספות.
בורוז[עריכת קוד מקור | עריכה]
ב-1886, ויליאם סיוורד בורוז (William Seward Burroughs, (אנ')), ייסד בסנט לואיס את "חברת האריתמומטר האמריקאית", בכוונה לייצר מכונות חישוב. בורוז החל לייצר ולמכור מכונות חיבור, שלא היו מכונות 4-פעולות, כפי שהשם "אריתמומטר" רומז. מכונות החישוב של בורוז השתמשו בלוח מקשים מלא, כמו הקומפטומטר, וכן במדפסת. בחלק מהמכונות המדפסת הייתה אמצעי הפלט היחיד, אבל ברובן היה חלון, בו ניתן לראות את התוצאה. גם אם המכונה של בורוז לא הייתה מכונת החישוב הראשונה עם מדפסת, היא הייתה כנראה הראשונה שבהן שהצליחה בשוק. החברה גדלה, והציגה דגמים נוספים. בורוז נפטר ב-1898, אבל החברה שיצר המשיכה לגדול. החברה עברה לדטרויט ב-1904, והמשיכה לייצר מכונות חישוב מדגמים שונים. במאה ה-20 נכנסה חברת בורוז לתחום המחשבים, והייתה אחת משבע החברות שהיוו את "הגמדים" בשוק המחשבים האמריקאי של שנות ה-60 וה-70, שכונה לפעמים "IBM ושבעת הגמדים". ב-1986 התאחדה בורוז עם חברת רמינגטון ראנד, ויחד יצרו את תאגיד יוניסיס, שעדיין קיים ב-2017.
כפל ישיר - ווראה, בולה, שטייגר וה"מיליונר"[עריכת קוד מקור | עריכה]
מכונות חישוב של ארבע פעולות, מבצעות כפל בעזרת חזרה על פעולת חיבור: כדי לכפול מספר ("הנכפל") ב-173 (הכופל), מחברים את הנכפל שלוש פעמים, מזיחים את התוצאה לעומת הנכפל, מחברים שבע פעמים, מזיחים שוב, ומחברים פעם נוספת. מספר פעולות החיבור הוא כסכום הספרות של הכופל – בדוגמה זו 1+7+3, כלומר 11 פעולות חיבור.
מכונת כפל ישיר היא מכונה שמבצעת כפל בספרה אחת בפעולה יחידה, כך שמספר הפעולות שיש לבצע הוא כמספר הספרות של הכופל, במקום סכום הספרות. החישוב בדוגמה הקודמת מתבצע במכונה כזו בשלוש פעולות, במקום ב-11. המכונות מבוססות על מימוש מכני של לוח הכפל.
הראשון שהדגים מכונת כפל ישיר שפעלה בהצלחה וסיפקה תוצאות נכונות היה הספרדי רמון ווראה (Ramón Verea), שבנה מכונה כזו ב-1877 בניו יורק, ורשם עליה פטנט אמריקאי ב-1878. ווראה לא הפך את המכונה למוצר, והשפעתה הייתה מוגבלת.
ב-1887 בנה צרפתי צעיר, לאון בולה (Léon Bollée), שהיה אז בן 17, שלוש מכונות חישוב משלושה סוגים שונים. אחת מהן ביצעה כפל ישיר. המכונה הוצגה בתערוכה העולמית של פריז ב-1889, וזכתה במדליית זהב. בולה בנה מספר דגמים של המכונה, ורשם מספר פטנטים על המכונה בארצות שונות. בולה לא המשיך לעסוק במכונות חישוב, ופנה עם אביו, לעיסוק בתחום הרכב המנועי, בו היה חלוץ וזכה להצלחה ניכרת, ומאוחר יותר עסק גם בתעופה. (כשהאחים רייט ביקרו בצרפת להדגמת מטוסיהם, בולה השאיל להם את השימוש במפעל המכוניות שלו בלה מאן). ב-1911 נפצע בולה בתאונת טיסה, פציעה ממנה לא החלים, וב-1913 נפטר.
המהנדס השווייצרי אוטו שטייגר (Otto Steiger) רשם ב-1892 מספר פטנטים במספר ארצות על מכונת כפל ישיר דומה למכונה של בולה. שטייגר פנה למהנדס האנס אגלי (Hans W. Egli) מציריך, וזה החל לייצר ב-1893 מכונת כפל ישיר לפי הפטנטים הללו, בשם מיליונר (Millionaire). עד 1935 יוצרו כ-5,000 מכונות, כשבמהלך הזמן נוספו למכונה שכלולים שונים כמו מנוע חשמלי, ולוח מקשים מלא. אגלי המשיך להיות יצרן חשוב של מכונות חישוב ופיתח מכונות נוספות במקביל לייצור ה"מיליונר". ניתן לקרוא הסבר מפורט וברור על אופן הפעולה של המכונה, בליווי תמונות, ומידע נוסף עליה במוזיאון הרשת של ג'ון וולף[6].
-
האריתמומטר של תומא במוזיאון הטכני של סטוקהולם
-
אריתמומטר אודהנר, שיוצר בסנקט פטרסבורג במאה ה-19
-
מכונת החישוב של בולדווין, מ-1885
-
"קופסת המקרוני". האבטיפוס של הקומפטומטר, שפלט בנה ב-1884.
-
קומפטומטר מודל ST, או Super totalizer. שנת ייצור משוערת – 1935
-
איור מפטנט אמריקאי 338110 של בורוז, 1888
-
בורוז. המדפסת מוסתרת, מאחור. מלפנים ה"חלון" דרכו נראית התוצאה.
-
מכונת כפל ישיר מיליונר: הזנת הקלט מתבצעת בעזרת המחלקים במרכז. את ספרות הכופל מזינים בעזרת המנוף בחלק השמאלי של המכונה, מסובבים את הארכובה (בחלק הימני) סיבוב אחד כדי לבצע את הכפל, וחוזרים על הפעולה עבור הספרות הנוספות. המכונה שוקלת למעלה מ-30 ק"ג
-
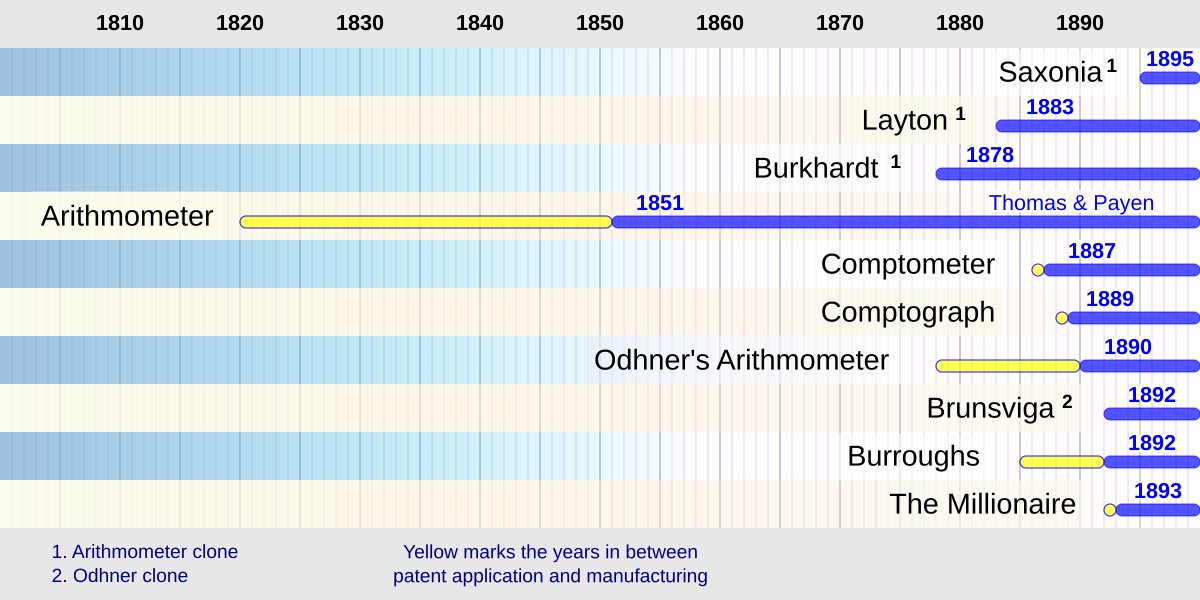
התפתחות מכונות החישוב העיקריות במאה ה-19 על ציר הזמן. האריתמומטר פותח את המירוץ בשנות העשרים עם דגמים ניסיוניים, ויוצא בגרסה מסחרית שמתחילה להימכר באמצע המאה. שלוש המכונות שמופיעות מעליו, הן שיבוטים שונים שלו. בנוסף למכונות בתרשים, פעלו יצרנים נוספים ברבות ממדינות אירופה, בארצות הברית, ובמדינות נוספות. מכונת החישוב החלה לבסס את מעמדה כאושיה בענף הציוד המשרדי, לצד מכונת הכתיבה והטלפון, שגילם דומה לגילה.
המאה העשרים[עריכת קוד מקור | עריכה]
בתחילת המאה ה-20 תעשיית מכונות החישוב הקיפה עשרות חברות במדינות רבות, בהן גרמניה, צרפת, אנגליה, איטליה, שווייצריה, רוסיה, שוודיה, וארצות הברית, ויצרנים חדשים הופיעו ביפן, סין, אוסטריה ועוד. מכונות ארבע פעולות ומכונות חיבור, עם ובלי הדפסה. "מפעיל מכונת חישוב" היה מקצוע מוכר, שנלמד בבתי ספר מקצועיים. בארצות הברית התעשייה התרכזה במכונות חיבור עם לוח מקשים מלא, ובאירופה רוב המפעלים התרכזו במכונות ארבע-פעולות, מבוססות על גלגל פינים או על תוף לייבניץ.
בתחילת המאה החלו יצרנים שונים לשלב מנוע חשמלי במכונות חישוב, בעיקר כדי לחסוך את הצורך בסיבוב הארכובה, ומאוחר יותר גם כעזר לפעולות נוספות, כמו איפוס והזחה. עד 1910 כבר הציעו יצרנים רבים באירופה "גרסה חשמלית" לחלק מהמכונות שלהם.
מכונות עשר ספרות[עריכת קוד מקור | עריכה]

באמצע המאה נפוצו מכונות חישוב בעלות עשרה מקשי ספרות, ולצידם מקשים נוספים לביצוע פעולות, בדומה ללוח המקשים של מחשבון. מכונות אלו התבססו על מנגנונים חדשים, בדרך כלל פסי שיניים ("rack and pinion") ו"תיבת פינים" (pinbox). במכונות מיצרנים שונים ניתן למצוא מנגנונים זהים, או כמעט זהים, ונראה שניתן היה לרכוש מנגנונים אלה מיצרני מכניקה (OEM), ולעצב סביבם מכונה עם לוח מקשים, עיצוב פיזי, הנעה, וכן הלאה. המכונות הללו היו רובן ככולן ממונעות, וביצעו פעולות כפל וחילוק באופן אוטומטי. לרבות מהן היה גם אוגר "זיכרון", אחד או יותר, בו ניתן לשמור תוצאות ביניים, ולהחזיר אותן אחר כך לאוגר הקלט או התוצאה, רבות מהן גם הדפיסו את החישובים והתוצאות, בדרך כלל על סרט נייר רציף. הפעלת מכונה כזו לא שונה בהרבה מהפעלת מחשבון מודרני פשוט.
יצרנים רבים, הן מהוותיקים בשוק והן חדשים הציעו מכונות אלו בדגמים רבים.
תכנון הנדסי מדויק, שיאן של יותר ממאה שנות אבולוציה, ושיטות ייצור מודרניות, אפשרו ליצרנים למכור מכונות משוכללות אלו במחיר תחרותי, אך שמשן זרחה מאוחר מדי, והן הפכו מיושנות, עם שאר מכונות החישוב המכניות, זמן קצר אחרי שהופיעו.
למידע נוסף על דור המכונות הזה, ראו באתר של ג'והן וולף.[7]
ארצות הברית[עריכת קוד מקור | עריכה]
ב-1902 החלה חברת דלטון האמריקאית למכור מכונות חיבור עם הדפסה, עם לוח מקשים של 10 ספרות (במידה מסוימת בדומה למחשבונים המקובלים היום, אם כי סידור הספרות שונה), ובכך למעשה סימן את תצורת הקלט השלישית המקובלת במכונות חישוב, אחרי המחלקים או המנופים, עם מחלק לכל ספרה של הקלט (כלומר שישה מנופים במכונה עם קלט של 6 ספרות וכן הלאה), ולוח המקשים המלא, כלומר ספרות 1 עד 9 עבור כל ספרה של הקלט, לוח מקשים של 10 ספרות היא צורת הקלט המקובלת השלישית, עם הספרות 0 עד 9, כשמשתמשים באותם עשרה מקשים להזנת כל ספרות הקלט, זו אחר זו. מכונה כזו מתאימה פחות ממכונה בעלת לוח מקשים מלא (דוגמת הקומפטומטר) לחיבור טורי מספרים ארוכים, משום שבעזרת לוח מקשים מלא יכול מפעיל מיומן יכול להזין מספרים מהר יותר ויעיל יותר, תוך הזנת מספר ספרות באותו זמן, בעזרת שימוש במספר אצבעות משתי הידיים. יתרונה של מכונת דלטון על מכונה עם לוח מקשים מלא הוא גודלה המצומצם יחסית, והמחיר.
ב-1911 פנה איש העסקים האמריקאי מונרו (Jay Randolph Monroe) לבולדווין, שמאז שהמציא את גלגל הפינים ב-1874 (במקביל לאודהנר) רשם המצאות רבות בתחומים שונים, מהן גם בתחום מכונות החישוב, והציע לו לפתח ביחד מכונת חישוב שתשלב את היתרונות של לוח מקשים מלא, שעד אז היה בשימוש במכונות חיבור בלבד, עם היכולות של מכונת ארבע פעולות. בולדווין ומונרו פיתחו את המכונה בהצלחה, וב-1912 נפתחה "חברת מכונות החישוב מונרו" (Monroe Calculating Machine Company) שהייתה הראשונה להציע מכונה בתצורה ששלטה בתחום עד תום עידן מכונות החישוב: מכונת ארבע פעולות עם לוח מקשים מלא. חברת מונרו המשיכה לייצר מכונות חישוב עד תום העידן, והיא קיימת עד היום (בשם "מונרו") ומשווקת ציוד משרדי, כולל מכונות חישוב אלקטרוניות.
באמצע המאה פעלו בארצות הברית שלושה מפעלים חשובים למכונות חישוב ("שלושת הגדולים") – מונרו, מרצ'נט ופרידן.
ב-1958 נקנתה מרצ'נט על ידי יצרנית מכונות הכתיבה סמית' קורונה (Smith Corona), שבעקבות כך שינתה את שמה ל-Smith Corona Marchant, ומאוחר יותר SCM. החברה המשיכה לפתח ולייצר מיכון משרדי, כולל מכונות חישוב, בעשור הבא.
שלושת החברות פיתחו מכונות חישוב אלקטרוניות, והיו בין הראשונות לעשות זאת. ב-1965 כבר היו לשלושתן מכונות כאלה. דגמים אלו היו נוחים יותר לשימוש, ואולי הדבר החשוב ביותר - שקטים, אך הם היו מוגבלים ויקרים, ולא זכו להצלחה מסחרית משמעותית.
פרויקט מנהטן[עריכת קוד מקור | עריכה]
בפרויקט מנהטן, פותחו שיטות לביצוע חישובים מורכבים, כולל שיטות לאנליזה נומרית, בעזרת "מחשבים אנושיים" (Human Computer), שהשתמשו במכונות חישוב מכניות ממונעות של מרצ'נט ופרידן[8].
רוסיה וברית המועצות[עריכת קוד מקור | עריכה]
ברוסיה פעלה עד מהפכת 1917 החברה של אודהנר. במהפכה (ייתכן שכבר בפרוץ מלחמת העולם הראשונה) הייצור נפסק. יורשיו של אודהנר חזרו לשוודיה, והחלו לייצר מכונות חישוב בשם "אודהנר מקורי" (Original Odhner). פליקס דזרז'ינסקי, שמאוחר יותר ייסד את שירות הביטחון צ'קה, השמיש את הציוד והוסיף עליו, והמפעל החל לייצר מכונות חישוב שכונו "פליקס", שם שהפך בסופו של דבר לשמה הרשמי של המכונה. מכונות פליקס יוצרו עד 1978, מספר שנים אחרי הפסקת ייצור מכונות חישוב מכניות במערב. במשך כ-50 שנות הפעילות יוצרו בברית המועצות כמה מיליוני מכונות פליקס, כנראה יותר מכל דגם של מכונה אחרת בעולם.
גרמניה[עריכת קוד מקור | עריכה]
גרמניה היא המדינה השנייה, אחרי צרפת, בה קמה תעשיית מכונות חישוב, וגרמניה הפכה מרכז חשוב של התעשייה הזו. התעשייה הגרמנית נוסדה בעיירה גלאסהיטה (Glashütte) על ידי ארתור בורקהארט, שהחל בייצור "תואמי אריתמומטר" ב-1885. מאוחר יותר, רכשה חברה בעיר בראונשווייג את הזכויות לייצר מכונות מסוג "אודהנר". החברה קראה למכונה "בראונשווייגה" על שם העיר, וזמן לא רב אחר כך החברה עצמה שינתה שמה לשם זה. בראונשווייגה נודעה כמכונה אמינה ביותר, והייתה המכונה הפופולרית והנפוצה ביותר מטיפוס "אודהנר" במשך שנים רבות. במאה העשרים נוסדו ושגשגו עוד חברות בתחום מכונות החישוב, וחברות שעסקו בתחומים אחרים נכנסו לתחום זה כדי לגוון את עסקיהם. בגלסהיטה, שם החלה התעשייה, קמו חברות נוספות, והעיירה הייתה זמן מסוים מרכז לתעשייה הזו, מעין "עמק הסיליקון" של מחשבים מברזל. חברת מכונות הכתיבה "מרצדס" (לא לבלבל עם דיימלר AG, שמייצרת מכונית בשם זה) שכרה את הממציא הפורה קרישטל האמאן (Christel Hamann), שכבר המציא ופיתח מספר מכונות חישוב מעניינות, אך ללא הצלחה שיווקית, לפתח מכונת חישוב חדשה. האמאן המציא מנגנון חדש, המבוסס על מערכת גלגל ופס שיניים (rack and pinion), והחברה פתחה קו מכונות חישוב בשם "מרצדס אויקליד" (Mercedes Euklid). חברת וולטר לייצור נשק קל ספורטיבי (החברה ידועה בין השאר בכך שייצרה את הנשק החביב על ג'יימס בונד, ה-PPK), החליטה לגוון את תחום פעילותה והחלה לייצר מכונות חישוב בצלה-מהליס (Zella-Mehlis) בשנות ה-20 של המאה. בעיירה סמרדה (Sömmerda) הקימה חברת החימוש ריינמטאל, שבעקבות הסכם ורסאי הייתה חייבת לעבור לייצור מוצרים אזרחיים, מפעל לייצור מכונות כתיבה ומכונות חישוב. בקמניץ החלה חברת "אסטרהוורקה" (Astrawerke) לייצר מכונות חישוב והדפסה מטיפוס "דלטון" בשם "אסטרה" (Astra). חברת הטלפון הגרמנית דה-טה-ווה (De-Te-We, מאוחר יותר DTW) שכרה את הממציא קרישטל המאן (מי שפיתח אמ האויקליד עבור חברת מרצדס), כדי שיפתח עבורה מכונת חישוב. קו המכונות שפיתח נקרא "האמאן מאנוס" (Hamann Manus). מכונות אלו נראות דומות למכונות מטיפוס "אודהנר", אבל הן מבוססות על עיקרון מכני שונה. כל המכונות בקו המאן מאנוס תומכות בחילוק אוטומטי. במוסף לחברות שהוזכרו, פעלו בתחום בגרמניה בין שתי מלחמות העולם עשרות, אם לא מאות חברות נוספות[2]
- שוודיה
אודהנר מקורי, פסיט (FACIT, מאוחר יותר Facit)
- שווייצריה
אגלי – מיליונר ו-MADAS, ארליקון
- אוסטריה
- איטליה
- אנגליה
לייטון, טייט, בל פאנץ'
- יפן
טייגר, ניפון, ביזיקום
- סין
גלריה[עריכת קוד מקור | עריכה]
-
מכונת חישוב סובייטית "פליקס", שהייתה בשימושם של ראשוני מתיישבי הוד השרון
-
מונרו, 1912: מונרו היה היצרן הראשון ששילב לוח מקשים מלא עם מכונה של ארבע פעולות
-
"אודהנר מקורי": מכונה שוודית של יורשי וילגודט אודהנר
-
מכונת ברונשוויגה ״עירומה״, שדפנותיה הוסרו, והמנגנונים גלויים לעין
-
מכונת חיבור והדפסה דלטון, המכונה המוצלחת הראשונה שהציגה לוח מקשים של 10 ספרות, החל מ-1902, בתצורה ייחודית (בשורה התחתונה 1 3 0 6 8, בשורה העליונה 2 4 5 7 9)
-
מכונת החישוב הסובייטית "פליקס". המכונה יוצרה מ-1929 ועד 1978, כמה שנים אחרי שכמעט כל היצרנים האחרים סגרו את פסי הייצור. מכונה בסיסית ופשוטה, עם הפונקציונליות הבסיסית בלבד, וכתוצאה מכך גם עמידה ואמינה. מספר המכונות שיוצרו נמדד במיליונים. מחיר המכונה ב-1959 היה 110 רובל סובייטי, שווה ערך לכ-30 דולר אמריקאי.
עקרונות פעולה[עריכת קוד מקור | עריכה]
פרט למספר קטן של יוצאי דופן, אפשר לחלק את מכונות החישוב לשני סוגים. הסוג הראשון הן מכונות שניתן לראות כפיתוח של הפסקלין, והסוג השני הן מכונות שאפשר לתאר כאבולוציה של מחשב הפסיעות של לייבניץ.
במכונות מהסוג הראשון, פעולת הזנת הקלט גורמת לביצוע הפעולה, חיבור או חיסור. לעומת זאת, בסוג השני, הקלט המוזן נשמר במכונה, ב"צובר הקלט", ונדרשת פעולה נוספת, בדרך כלל סיבוב ארכובה, או מאוחר יותר הנעה בעזרת מנוע, כדי לבצע את הפעולה, ולעדכן את "צובר התוצאה".
המכונות מהסוג הראשון בדרך כלל מוגבלות לחיבור בלבד, או חיבור וחיסור, בעוד שבמכונות מהסוג השני ניתן להשתמש כדי לבצע חיבור, חיסור, כפל וחילוק, והן מכונות "מכונות חישוב של ארבע פעולות". האריתמומטר של תומא ומכונת החישוב של אודהנר הן מסוג זה, וכמוהן המכונות שהתפתחו מהן.
מכונות מהסוג הראשון נקראות "מכונות חיבור" או "מכונות חיבור והדפסה". הקומפטומטר ומכונות החישוב של בורוז הן מסוג זה, ולמעשה רוב או כל הקופות הרושמות בעידן הטרום-אלקטרוני, היו מכונות חישוב מסוג זה, שנוספה אליהן מגירה לשטרות, מטבעות, המחאות וקבלות.
עקרונות הפעולה של מכונות ארבע פעולות[עריכת קוד מקור | עריכה]
מכונת ארבע פעולות אופיינית מכילה שלושה צוברים. בחלק מהמכונות המשוכללות יותר יש צוברים נוספים, אך גם הן מכילות את שלושת הצוברים המתוארים:
- צוברים
- צובר הקלט: מפעיל המכונה מזין את המספר עליו יש לבצע את הפעולה לצובר זה. במהלך השנים פותחו שיטות שונות להזנת הקלט הנפוצות הן:
- מנופים או מחלקים: האריתמומטר של תומא השתמש במנופים, או מחלקים, כשלכל ספרה של צובר הקלט יש מחלק נפרד, כלומר מחלק אחד ליחידות, שני לעשרות, שלישי למאות וכן הלאה. המפעיל מסיט את המחלק למיקום המתאים לספרה. כמוהו גם המכונה של אודהנר והמכונות שהתפתחו ממנה
- במכונות מאוחרות יותר (החל מהמכונה של מונרו) הקלט מוזן על ידי לוח מקשים מלא, עם עמודת מקשים לכל ספרה – עמודה אחת ליחידות, שנייה למאות, שלישית לאלפים וכן הלאה בכל טור ספרות מ-1 עד 9. עבור 0 המפעיל לא לוחץ על אף מקש בעמודה.
- לוח מקשים בן עשרה מקשים, מ-0 עד 9 בדומה למקשים המוכרים ממכונות חישוב ומחשבונים בני ימינו.
- מונה, מכונה גם "המנה", משום שצובר זה מראה את התוצאה בסיום פעולת חילוק: המונה סופר את מספר הפעולות שבוצעו: בפעולת חיבור, המונה סופר את מספר המחוברים: למשל עבור 123 + 234 + 47, המונה יראה "3" בסיום הפעולה. בסיום פעולת כפל המונה מראה את הכופל (הנכפל הוזן לצובר הקלט), ובסיום פעולת חילוק, המונה מראה את המנה (כלומר תוצאת הפעולה). מכונות שונות נבדלות לגבי תוכן המונה בסיום פעולת חיסור.
- צובר התוצאה. מונה זה מראה את התוצאה בסיום פעולת חיבור, חיסור או כפל. בפעולת חילוק, המחולק מוזן לצובר התוצאה לפני הפעולה, והמחלק לצובר הקלט. בסיום הפעולה, המנה מופיעה במונה, וצובר התוצאה מכיל את השארית.
הפעולה הבסיסית של מכונת ארבע פעולות היא חיבור או חיסור. העובדה שצובר הקלט לא מנוקה אחרי הפעולה, מאפשרת לחזור בקלות יחסית על הפעולה מספר פעמים, ועל ידי כך לבצע כפל. אם נבצע את הפעולה 7 פעמים, המונה יראה "7", והתוצאה תראה את הקלט מוכפל ב-7.
- הפעלה
האריתמומטר והמכונות שהתפתחו ממנו מצוידות בארכובה, והפעולה הבסיסית של מכונות החישוב, כלומר חיבור תוכן הקלט לתוצאה, מתבצעת בעזרת סיבוב הארכובה פעם אחת. לארכובה יש "מצב אפס", או מצב מוצא, וכל פעולה מתחילה ומסתיימת כשהארכובה במצב זה. מכונות חישוב רבות מכילות מנגנונים שתפקידם לנעול את המכונה (כלומר למנוע כל שינוי במצב המכונה) כאשר הארכובה לא במצב אפס. יש מכונות בהן פעולת חיסור מתבצעת על ידי הנעת הארכובה בכיוון הפוך, ואחרות בהן הארכובה יכולה לנוע רק בכיוון אחד. במכונות מאוחרות יותר, מנוע חשמלי מחליף את הארכובה. גם במכונות אלו, הפעולה מתבצעת על ידי סיבוב ציר כלשהו סיבוב אחד בדיוק. בדרך כלל המנוע מסתובב באופן רצוף, ומצמד מכני משלב ומנתק את המנוע מציר זה, ומבטיח שהמכונה תחזור ל"מצב אפס" בסיום כל פעולה.
- הזחה
בעזרת המכונה כפי שתוארה עד כאן כבר ניתן לבצע כפל: למשל, כדי לכפול 12345 ב-13, אפשר להזין 12345 בצובר הקלט, ואז לסובב את הארכובה 13 פעמים. כשהכופל גדול מספיק, שיטה זו לביצוע כפל אינה מעשית, גם אם היא אפשרית. כל המכונות שמבוססות על המכונה של לייבניץ מכילות מנגנון שמאפשר להזיח את צובר התוצאה יחסית לצובר הקלט: אם צובר הקלט מראה "7", פעולה אחת (כלומר סיבוב יחיד של הארכובה) מוסיפה לצובר התוצאה 7 כשהמכונה נמצאת במצב הזחה 1, או "יחידות". במצב הזחה 2 (עשרות), פעולה אחת תוסיף 7 לספרת העשרות של צובר התוצאה, ובסיום הפעולה הוא יראה "70". במצב הזחה 3, פעולה אחת מוסיפה לתוצאה 700, וכן הלאה. גם המונה לוקח את מצב ההזחה בחשבון: בהזחה 1, פעולה אחת מקדמת את המונה ב-1, במצב הזחה 3, פעולה אחת מקדמת את המונה ב-100. אפשר לראות שמצב המכונה אחרי 1,000 סיבובים של הארכובה במצב הזחה, זהה למצב המכונה אחרי סיבוב יחיד של הארכובה במצב הזחה 4: המונה מכיל 1,000, והתוצאה מראה את הקלט מוכפל ב-1,000.
- איפוס
לפני התחלת חישוב חדש, יש לאפס את התוצאה והמונה. אם לא עושים זאת, תוצאת החישוב החדש תתווסף לתוצאה ולמונה הקיימים. במכונות שונות יש מנגנונים שונים לאיפוס, ומכונות רבות יש גם מנגנון לאיפוס צובר הקלט. בדרך כלל האיפוס מתבצע על ידי הסטת מנוף או סיבוב ארכובה נוספת. בדרך כלל יש שני מנופים נפרדים, לאיפוס התוצאה ולאיפוס המונה, אך יש מכונות בהן מנוף אחד מאפס את שני הצוברים, ובעזרת מנוף שני המפעיל יכול לקבוע אם הפעולה תנקה את שני הצוברים, את המונה בלבד או את התוצאה בלבד. במכונות עם מנוע חשמלי, בדרך כלל יש כפתורים שלחיצה עליהם משלבת את המנוע לאיפוס אחד הצוברים או שניהם.
ביצוע ארבע פעולות החשבון[עריכת קוד מקור | עריכה]
התיאור מתייחס בדרך כלל למכונות ידניות. מכונות חשמליות פועלות באותו אופן, אבל יכולות להיות שונות לגבי האופן בו המפעיל גורם לפעולה, למשל על אילו כפתורים יש ללחוץ, ובאיזה סדר, וכן הלאה.
- חיבור
כאמור, הפעולה הבסיסית של כל המכונות היא פעולת החיבור. פעולת החיבור מתבצעת כלהלן:
- איפוס התוצאה והמונה
- הזנת המחובר הראשון לקלט
- הפעלה (סיבוב הארכובה או לחיצה על כפתור במכונה חשמלית)
- חזרה על פעולה 2 ו-3 עבור שאר המחוברים
בסיום הפעולה, המונה יראה את מספר המחוברים (2 או יותר), ובתוצאה יופיע הסכום
- חיסור
- חיבור המחוסר כמו המחובר הראשון בפעולת חיבור; בסיום הפעולה המחוסר מופיע בצובר התוצאה
- הזנת המחסר לצובר הקלט
- ביצוע הפעולה: במכונות שונות פעולת חיסור מתבצעת בצורות שונות. במכונה של אודהנר, כמו בהרבה מכונות מסוג אודהנר של יצרנים אחרים, מסובבים את הארכובה בכיוון הפוך כדי לבצע חיסור. במכונות אחרות המכונה מועברת למצב "חיסור" (בדרך כלל על ידי הסטת מנוף, מנופים, לחיצה על כפתור, או באופן אחר (למשל כדי להעביר את הקורטה למצב חיסור, יש למשוך את הארכובה כמה מילימטרים בכיוון ציר הסיבוב), והפעלת המכונה כמו בפעולת חיבור.
- כפל
- איפוס צוברי התוצאה והמונה
- הזנת הנכפל לצובר הקלט
- מצב הזחה 1 (יחידות)
- הפעלת המכונה מספר פעמים כספרת היחידות של הכופל
- הגדלת ההזחה ב-1
- חזרה על פעולות 4 ו-5 עבור כל ספר נוספת של הכופל, כלומר ספרת העשרות, המאות וכן הלאה.
- בסיום, המכפלה מופיעה בצובר התוצאה, הנכפל בצובר הקלט, והכופל במונה.
כדי לכפול 12,345 ב-462, יש להזין 12,345 בצובר הקלט, לנקות את התוצאה והמונה, ולהזיח למצב 1 (יחידות), ומסובבים את הארכובה פעמיים. המונה מראה 2. מזיחים למצב "1" (עשרות), ומסובבים את הארכובה 6 פעמים. המונה מראה 62. מזיחים למצב "2", ומסובבים את הארכובה 4 פעמים. במונה מופיע 462. בכל מצבי הביניים (כלומר אחרי כל סיבוב של הארכובה), התוצאה תמיד מראה את המכפלה של הקלט במונה. יש המתייחסים לביצוע כפל כ"פיתוח" המונה: במקום לספור סיבובים, המפעיל מסובב את הארכובה עד שהמונה מראה את הערך המבוקש לספרה הנוכחית, והזחה לספרה הבאה. מכונות מסוימות תומכות ב"כפל מקוצר": למשל כדי לכפול ב-199, יש לסובב את הארכובה 19 פעמים: תשע פעמים עבור היחידות, עוד תשע עבור העשרות, ופעם אחת עבור המאות. ב"כפל מקוצר" המפעיל משלב, לפי הצורך, פעולות חיבור וחיסור בהזחות השונות: במקרה הזה, המפעיל מבצע את הפעולה פעמיים (במקום אחת) בהזחת המאות, אין כלל צורך לבצע פעולה עבור הזחת העשרות, ובהזחת היחידות מבצעים פעולת חיסור יחידה, במקום חיבור: הפעולה מחסרת אחד מן המונה, שהראה 200, כך שאחרי הפעולה המונה מראה 199, מה שרצינו. לתוצאה לא צריך לדאוג – היא תמיד מציגה את המכפלה של המונה בקלט, כך שאחרי הזנת הקלט, יש "לדאוג" רק למונה. לא כל המכונות תומכות בכפל מקוצר, וההבדל מוסבר בסעיף "תכונות נוספות".
- חילוק
יש יותר מדרך אחת לבצע חילוק. נתאר אחת מהן:
- איפוס
- הזנת המחולק לצובר התוצאה. אפשר לעשות זאת בעזרת פעולת חיבור אחת, שאחריה מאפסים את המונה. יש מכונות בהן ניתן לכוון את צובר התוצאה ישירות, למשל בעזרת סיבוב מחוונים. כדי לקבל דיוק מיטבי, כלומר מספר ספרות עשרוניות בתוצאה גדול ככל האפשר, מזינים את המחולק כך שהספרה המשמעותית ביותר שלו היא הספרה העליונה בצובר התוצאה, לפי המכונה (מספר הספרות בצובר התוצאה הוא אחד המאפיינים החשובים של מכונת חישוב, ובדומה גם של מחשבונים אלקטרוניים)
- הזנת המחלק לצובר הקלט.
- הזחה למצב ההזחה המרבי כך שניתן לבצע פעולת חיסור בלי גלישה (מצב שמתרחש כשמחסרים ממספר מסוים מספר גדול ממנו: התוצאה שלילית, אבל בצובר התוצאה של מכונת חישוב אין דרך להציג מספרים שליליים, והמספר שמוצג הוא המשלים ל-10). ניתן לזהות את המצב הזה, משום שפעולת ההזחה מציבה את צובר הקלט מתחת (או מעל) צובר התוצאה בהזחה הנכונה, כלומר אם מדמיינים עוד אפסים מימין לצובר הקלט, אפשר בקלות לראות איזה משני המספרים גדול יותר,
- ביצוע פעולות חיסור עד שהקלט גדול מהתוצאה (כלומר עד הרגע שחיסור נוסף יגרום לגלישה)
- הקטנת ההזחה ב-1, וחזרה ל-5
- החילוק מסתיים כאשר יש אפס בצובר התוצאה, או כשלא ניתן להזיח, כלומר המכונה במצב הזחה "1".
בסיום פעולת החילוק, המנה (תוצאת החישוב) מופיעה במונה, ואילו צובר התוצאה מכיל אפס, כאשר המחולק אכן מתחלק במחלק. אם המספרים לא מתחלקים זה בזה, צובר התוצאה מכיל את שארית החילוק. משום שהפעולה החלה במצב הזחה כלשהו וגם המחלק הוזן לקלט מוזח בחלק מהמקרים, מיקום הנקודה העשרונית משנה: המנה, שמופיע במונה של המכונה, תהיה בדרך כלל מספר עם שבר עשרוני, ומהמפעיל מחשב את מיקום הנקודה העשרונית – הפרש המיקומים של הנקודה העשרונית בתוצאה (כלומר המחולק) והמחלק.
מבנה מכונות ארבע פעולות[עריכת קוד מקור | עריכה]
למכונה שני חלקים – גוף ועגלה.
- גוף
גוף המכונה ניצב על השולחן (בדרך כלל), ומכיל את מנגנון הקלט ואת מנגנוני ההנעה של המכונה, בדרך כלל ארכובה או מנוע, מצמדים, ותמסורות. בנוסף, הגוף מכיל את צובר הקלט ומערכת הקלט, ואת רוב הפקדים של המכונה, למשל בורר מצב חיבור/חיסור, ובמכונות מתקדמות יותר, את הפקדים ששולטים על הפעולות המתקדמות, כגון חילוק אוטומטי, כפל אוטומטי, ואפילו הוצאת שורש ריבועי.
התפקיד העיקרי של הגוף הוא להוסיף את הערך של צובר הקלט לצובר התוצאה, שנמצא בעגלה. זה מתבצע בעזרת אחד מכמה מנגנונים. במהלך השנים הוצעו ונבנו מנגנונים שונים להוספת הקלט לתוצאה. רק חלק קטן מהמנגנונים האלו היה "מוצלח", כלומר הותקן במכונות חישוב שיוצרו במספרים משמעותיים ופעלו בצורה אמינה. מרבית מכונות החישוב השתמשו באחד משני מנגנונים: תוף הפסיעות או גלגל הפינים. שני המנגנונים העיקריים מיוחסים ללייבניץ: למעשה, מנגנון תוף הפסיעות מכונה "גלגל לייבניץ", והוא תיאר בכתב גם את מנגנון גלגל הפינים. כאמור, כמעט כל מכונות החישוב של ארבע פעולות מבוססות על אחד משני המנגנונים, עם מספר יוצאי דופן חשובים, שמתוארים בהמשך.
- עגלה
העגלה מותקנת על מסילה לרוחב המכונה, מעל או מתחת למנגנון הקלט. המסילה מאפשרת לעגלה תנועה ימינה ושמאלה, בין מספר מצבים מוגדר. הזזת העגלה ממצב למצב נקרא "הזחה", ומספר המצבים האפשריים של העגלה הוא אחד ממאפייני המכונה, בדרך כלל זהה למספר הספרות במונה. העגלה מכילה את צובר התוצאה, ואת מנגנון הנשא. מונה הסיבובים נמצא בעגלה במכונות מסוימות, ובגוף המכונה באחרות. העגלה בדרך כלל מכילה, מלבד שני הצוברים, גם את מנגנון האיפוס שלהם, ולפעמים מחוונים ("Twirlers") כדי להזין בצובר התוצאה את המחולק, בהכנה לפעולת חילוק.
מצבי העגלה מייצגים את המימוש המכני של פעולת ההזחה שהוזכרה בתיאור הפעולות. במצב "1", ספרת היחידות של צובר הקלט (בגוף) ניצבת מול ספרת היחידות של התוצאה (בעגלה), במצב זה, פעולה אחת מוסיפה את תוכן הקולט לצובר התוצאה. במצב הזחה "2", העגלה מוזחת ספרה אחת ימינה, כך שספרת העשרות של צובר התוצאה נמצאת מול ספרת היחידות של הקלט. פעולה אחת במצב זה מוסיפה את הקלט מוכפל ב-10 לתוצאה. במצב הזחה "3" ספרת המאות של התוצאה מתאימה לספרת היחידות של הקלט, ופעולה אחת מחברת את הקלט מוכפל ב-100 לתוצאה, וכן הלאה: במצב 4 פעולה מוסיפה את הקלט מוכפל ב-1,000, במצב 5 ב-10,000, וכולי. במצב הזחה 1, המונה מקודם ב-1 עבור כל פעולה, ושוב, לפי ההזחה פעולה של המכונה מוסיפה 1 למונה הסיבובים, וגם כאן, כל הזחה מכפילה ב-10: במצב הזחה 4, פעולה אחת של המכונה מקדמת את המונה ב-1,000.
העגלה מכילה את צובר התוצאה והמונה, ובדרך כלל גם את מנגנון הנשא, שיתואר בהמשך. כל צובר כזה מורכב משורת גלגלים, כשעל היקפו של כל גלגל רשומות הספרות מ-0 עד 9. כל גלגל מונע על ידי מערכת תמסורת כלשהי המורכבת מגלגל שיניים אחד או יותר, כאשר יש פתח, או חלון, שנמשך לאורך שורת הגלגלים דרכו ניתן לראות ספרה אחת מכל גלגל. כל ביצוע "פעולה" של המכונה, מקדם את הגלגל המתאים במספר שווה למספר המופיע בספרת הקלט שניצבת כרגע מול ספרה זו. כשספרה מסוימת מתקדמת מ-"9" ל-"0", מנגנון הנשא מסמן שצריך להוסיף אחד לספרה הבאה. מונים מכניים כאלו מוכרים לנו למשל ממד מרחק מכני שהיה נהוג במכוניות עד בערך תום המאה ה-20, מדי מים, ומוני חשמל הנהוגים עד היום. במדים אלו, רק הספרה האחרונה נעה, והספרות הבאות מונעות רק על ידי הנשא, כלומר ספרת העשרות מתקדמת רק כשספרת היחידות עוברת מ-9 ל-0, ספרת המאות מקודמת רק כשספרת העשרות גולשת, וכן הלאה. צובר התוצאה של מכונת החישוב לא יכול להשתמש במנגנונים כאלו, משום שכל הספרות מונעות באותו זמן, וקשה לבנות מנגנון שישלב את הקידום כתוצאה מנשא שמגיע מימין (כלומר מהספרה הקודמת), עם הקידום שמגיע מהקלט. לכן, מנגנון הנשא במכונת חישוב מסובך יותר מהמנגנון בשעון מים או במד מרחק.
- נשא
הדרך בה פותרות מכונות החישוב את הבעיה שתוארה, היא על ידי חלוקת מחזור ה"פעולה" למספר חלקים. בחלק הראשון, נוסף הערך של הקלט לתוצאה (והמונה מקודם ב-1). בזמן ביצוע הפעולה, מסמנת כל ספרה האם יש צורך להעביר נשא לספרה הבאה. בחלק הבא, מופעל מנגנון הנשא. המנגנון לא מופעל על כל הספרות באותו הזמן, משום שהוספת הנשא לספרה מסוימת יכולה לגרום לנשא לספרה הבאה ("נשא מתגלגל").
נדגים בדוגמה:
- פעולה 14445 + 38455.
| הדגמת פעולה: 14445 (התוכן הנוכחי של צובר התוצאה) 38455 + (צובר הקלט) | |||
|---|---|---|---|
| שלב | צובר התוצאה | אילו ספרות סימנו (או "שלחו") נשא לספרה שאחריהן | הערות |
| אחרי הזנת המחובר הראשון | 14445 | אף ספרה לא שלחה נשא לספרה הבאה | אחרי חיבור המחובר הראשון, המפעיל מאפס את הקלט, ומזין בו את המחובר השני: 38455. במכונות רבות (אך לא בכולן), ביצוע פעולת החיבור, גורם לאיפוס את הקלט באופן אוטומטי. |
| אחרי חיבור צובר הקלט (המחובר השני), ולפני התחלת עיבוד הנשא | 42890 | היחידות והאלפים | היחידות (5+5) והאלפים (4+8) עברו מ-9 ל-0 תוך ביצוע הפעולה, וסימנו נשא לספרות הבאות (ספרת האלפים המשיכה להתקדם אחרי שליחת הנשא) |
| אחרי עיבוד הנשא של ספרת היחידות | 42800 | המאות והאלפים | בעיבוד הנשא של היחידות, ספרת העשרות עברה מ-9 ל-0, וסימנה נשא למאות. הנשא של האלפים עדיין לא עובד. |
| אחרי עיבוד הנשא של העשרות | 42900 | אלפים | ספרת המאות התקדמה מ-8 ל-9, ולא יצרה נשא חדש. |
| אחרי עיבוד הנשא של המאות | 42900 | אלפים | ספרת המאות לא שלחה נשא, ומחזור "עיבוד הנשא של המאות" לא שינה את התוצאה. |
| אחרי עיבוד הנשא של האלפים | 52900 | הנשא של האלפים עובד, וספרת עשרות האלפים התקדמה מ-4 ל-5. למעשה החישוב המסוים הזה הסתיים, אבל המכונה ממשיכה לגלגל את הנשא (הריק, במקרה זה) קדימה לספרות הבאות, לפי אורך צובר התוצאה. | |
מבחינה מכנית, החלק הראשון, של חיבור כל ספרות הקלט בו-זמנית אורך בדרך כלל בין מחצית לשני שלישים הפעולה, וגלגול הנשא מתבצע במהירות, ספרה אחרי ספרה, בחלק השני של המחזור. פעולה שלמה מורכבת תמיד (חוץ מאשר במכונות "תמסורת רציפה"), משני חלקי הפעולה זה אחר זה. רצף עיבוד הנשא נקרא "נשא מתגלגל" (ripple carry). יש הבדל קטן בין אופן פעולה זה, והאופן בו בדרך כלל מלמדים לבצע פעולת חיבור בין מספרים מרובי ספרות בבית הספר: בדרך כלל, כשמחברים מספרים בעזרת נייר ועפרון, מחברים כל הספרות הספרות זו אחר זו, ובד בבד מוסיפים, אם צריך, את הנשא מהספרה הקודמת. משמעות הדבר היא, שכאשר יש נשא אנו מחברים למעשה שלוש ספרות (הספרה המתאימה מכל אחד מהמחוברים, ו-"1" מהנשא). כדי לממש זאת באופן מכני, נחוץ מנגנון שמחבר (או "סוכם") תנועה משני מקורות שונים. מנגנונים כאלו קיימים, ונקראים דיפרנציאל. שימוש במנגנון כזה במכונת חישוב מעלה את הסיבוך ומספר החלקים באופן משמעותי.
רק יצרן אחד של מכונות חישוב, היצרן האמריקאי מרצ'נט (Marchant (אנ'), ואחרי 1958 "SCM") בחר בפתרון זה, כלומר שימוש בממסרים ודיפרנציאלים כדי להוסיף את הנשא תוך כדי צבירת הקלט, במקום מנגנון ה"נשא המתגלגל" שתואר לעיל, וכתוצאה, מכונות החישוב של מרצ'נט הן מורכבות ומסובכות ביותר, עם למעלה מ-4,000 חלקים, ותוצאה נוספת היא שהן גם מהירות יותר מכל מכונת חישוב מכנית אחרת, ופעולתן רועשת פחות. המכונות קיבלו את השם המסחרי "Silent Speed", כדי להדגיש זאת.
מנגנונים[עריכת קוד מקור | עריכה]
סעיף זה עוסק במנגנונים השונים שמשמשים לחיבור (או חיסור) תוכן צובר הקלט לצובר התוצאה. מכונות חישוב שונות מכילות מנגנונים רבים נוספים, שלא יתוארו כאן. רובן המכריע של מכונות חישוב "ארבע פעולות" עושות שימוש באחד משני המנגנונים שהוזכרו לעיל, ויתוארו בפירוט להלן. כמה יצרנים בנו מכונות שמשתמשות במנגנונים אחרים, ואלו יתוארו בקווים כלליים. שני המנגנונים העיקריים הם "תוף פסיעות", ו"גלגל פינים". המכונה הראשונה שנבנתה עם מנגנון תוף פסיעות היא מכונתו של לייבניץ. הוא גם תיאר את מנגנון גלגל הפינים, אם כי אין מידע על מכונה שנבנתה על ידו לפי עיקרון זה. במאה ה-17 וה-18 נבנו מספר מכונות לפי עקרונות אלו. האריתמומטר של תומא, והמכונות שנבנו בעקבותיו משתמש במנגנון תוף פסיעות, והאריתמומטר של אודהנר, והמכונות שנבנו בעקבותיו, מבוססים על גלגל הפינים.
- תוף פסיעות
מנגנון תוף הפסיעות מורכב משני צירים מקבילים. על ציר אחד מקובע התוף, ועל הציר השני יש גלגל שיניים זחיח, באופן שהגלגל מקובע לצירו מבחינה סיבובית, כלומר הגלגל והציר מסתובבים יחד, והגלגל ניתן להזחה לאורך הציר, כך שהוא ניצב מול חלק שונה של התוף בכל הזחה נתונה (ראו אנימציה למטה). לגלגל השיניים הזחיח יש "צווארון", שנאחז על ידי מזלג, והמזלג שולט על ההזחה, בלי להפריע לגלגל ולציר להסתובב. הזנת הקלט, מפעילה את המזלג, והגלגל מוזח לנקודה התואמת את הספרה שהוזנה.
בסיבוב מלא של התוף, גלגל השיניים יתקדם בין אפס לתשע שיניים, כתלות במיקומו לאורך הציר והתוף. ציר הגלגל משולב, בעזרת תמסורת שבנויה מגלגלי שיניים נוספים, עם אחד מגלגלי הספרות של התוצאה, כך שכאשר הגלגל מקודם כדי שן אחת, ספרת התוצאה המתאימה מתקדמת כדי ספרה אחת. כשספרת התוצאה "מתקדמת" מ-9 ל-0, היא "שולחת", או מסמנת, נשא לספרה הבאה. במכונה כזו יש בדרך כלל תוף פסיעות נפרד עבור כל ספרה של הקלט. מנגנון זה שימש במכונת החישוב המכנית המסחרית הראשונה (אריתמומטר), והמשיך לשרת במכונות חישוב של יצרנים רבים - דוגמת רהינמטאל בגרמניה, מונרו ופרידן בארצות הברית, ועוד עשרות יצרנים במדינות רבות בעולם, כולל הקורטה, דגם ממנו יוצרו מאות אלפי מכונות בליכטנשטיין, בין 1947 ועד 1970.
- גלגל פינים
גלגל הפינים (pinwheel) הוא למעשה גלגל שיניים, בו ניתן לשלוט על מספר השיניים, מנגנון זה ממומש בעזרת תשעה פינים (ומכאן השם), המותקנים בגלגל זה ליד זה, כך שכל פין מותקן לאורך רדיוס, כלומר ממרכז הגלגל להיקפו. לפינים חופש תנועה מסוים, כך שכשהפין מוזח החוצה ממרכז הגלגל, חלק ממנו בולט מעבר להיקף, ומהווה שן. מנגנון הקלט מושך חלק מהפינים פנימה ודוחף חלק מהם החוצה, כך שכשמזינים, למשל 4, ארבעה מתשעת הפינים בולטים החוצה, וגלגל הפינים מתפקד כגלגל שיניים עם ארבע שיניים. במכונה יש מספר גלגלי פינים, אחד עבור כל ספרת קלט. הגלגלים מותקנים על ציר אחד, ומהווים ביחד יחידה המכונה "רוטור". פעולה אחת של המכונה מתבצעת על ידי סיבוב מלא של הרוטור, כל שכל גלגל פינים מקדם את הספרה המתאימה בצובר התוצאה לפי מספר הפינים הבולטים, כלומר לפי ערך ספרת הקלט. זהו המנגנון הדומיננטי אצל היצרנים מגרמניה (ברונשוויגה, וולטר), שוודיה ("אודהנר מקורי", פסיט), ברית המועצות (פליקס), היפנים, והסינים.
- מנגנונים נוספים
במרוצת השנים, הומצאו מספר מנגנונים נוספים שיתוארו בקווים כלליים בלבד:
- כפל ישיר
- המנגנון הוזכר בקצרה בסעיף קודם. במנגנון זה, הקלט לא מוזן ישירות לתוצאה, ובמקום זה המכונה פועלת, לאחר הזנת הנכפל, בעזרת הזנת ספרות הכופל זו אחר זו, והפעלת המכונה בין כל שתי ספרות. המכונה משתמשת בייצוג מכני של לוח הכפל. דוגמה קצרה להסבר הפעולה: נניח שספרת קלט מסוימת (כלומר יחידות, עשרות, מאות וכולי) מכוונת ל-5. אם המפעיל יזין ככופל את הספרה "9". הפעולה מתבצעת בשני מחזורים: במחזור הראשון התוצאה תקודם ב-4 (ספרת העשרות של 9x5, כלומר 45), הנשא מעובד, ועגלה מוזחת מקום אחד שמאלה, התוצאה מקודמת ב-5 (ספרת היחידות), והנשא מעובד שוב. אם ספרת קלט אחרת מונחל, למשל, מול 9, התוצאה תקודם ב-8 בסיבוב הראשון, ולאחר הזחה שמאלה, ב-1. המכונה המסחרית היחידה שהתבססה על מנגנון הנעה זה, היא ה"מיליונר", שיוצרה על ידי חברת ההנדסה "אגלי" בציריך, שווייץ, בין 1893 עד בערך 1935. בסך הכל יוצרו בערך 5000 מכונות "מיליונר". כיום נמצאות רבות ממכונות אלו בידי אספנים פרטיים ומוזאונים[9]
- פסי שיניים יחסיים:
- במנגנון זה, תשעה פסי שיניים מבצעים תנועה מחזורית הלוך ושוב בכל פעולה, באופן שהפס הראשון מתקדם ונסוג כדי שן אחת, השני כדי שתי שיניים וכן הלאה. בהזנת הקלט, גלגל השיניים המתאים לכל ספרה ממוקם מעל אחד הפסים. מכונות החישוב של "מרצדס אויקליד" הגרמנית, לפי תכנון ופטנטים של הממציא כרישטל המאן, שיוצרו בין 1906, ל-1970[10], מונעות באמצעות מנגנון זה.
- גלגל רצ'ט:
- זהו מנגנון דומה מבחינה מסוימת לגלגל פינים: אף על פי שהוא מבוסס על עיקרון מכני שונה, מכונת חישוב של גלגל רצ'ט דומה מבחינה חיצונית, ובפרטים פנימיים רבים למכונת גלגל פינים. חברת דה-טה-ווה (DeTeWe, או "Deutsche Telephonwerke") ייצרה מכונות החישוב בשם "המאן-מאנוס" (Hamman Manus), המבוססת על מנגנון זה, לפי המצאה ופטנטים של כרישטל המאן. המכונות יוצרו החל ב-1925, ודגמים משוכללים יותר ויותר יוצרו ונמכרו עד תום עידן מכונות החישוב, בתחילת שנות ה-70 של המאה ה-20.
- תמסורת רציפה:
- המנגנון הזה מייצג אולי את פסגת מכונות החישוב המכניות המסחריות. בכל המנגנונים שהוזכרו קודם, הפעולה מתבצעת בצורה מקוטעת: חיבור הקלט לתוצאה מתבצע בחלק אחד של הפעולה, ומייד אחריו עיבוד הנשא. ברוב המנגנונים שהוזכרו (כולם פרט ל"פסי שיניים יחסיים"), ההנעה של הקלט מתבצעת באותה מהירות, ללא תלות בספרה שהוזנה, וההבדל בין הספרות השונות הוא במשך הזמן שהקלט מניע את התוצאה: אם למשל מזינים בקלט 91, ספרת היחידות תשולב לזמן קצר, וספרת העשרות תשולב לפרק זמן ארוך פי תשעה. בתמסורת רציפה, לעומת זאת, הקלט משולב עם התוצאה למשך כל הפעולה, והעברת הנשא מתבצעת באותו הזמן: כשמזינים במערכת זו 91, ספרת העשרות תונע פי 9 יותר מהר (בעזרת ממסרת שמשלבת את הספרה "בהילוך גבוה" יותר) מספרת היחידות, כששתיהן מונעות באופן רציף משך כל זמן הפעולה. כיוון שהנשא מעובד באותו הזמן, ניתן לבצע חיבור חוזר (שהיא הפעולה הבסיסית בכפל בכל המכונות פרט למכונות כפל ישיר) בצורה יותר מהירה, חלקה, ואמינה ופחות רועשת מכל מנגנון מסחרי אחר. מכונת החישוב האמריקאית "מרצ'נט", המונעת באמצעות מנגנון זה, לפי המצאה ופטנטים של המהנדס הרולד איברי (Harold T Avery), יוצרה בין 1932 ועד 1973, ונחשבה לפסגת מכונות החישוב. מכונות אלו מסובכות ומורכבות, ובנויות מאלפי חלקים.
גלריה[עריכת קוד מקור | עריכה]
-
אנימציה של מנגנון "גלגל לייבניץ". גלגל השיניים המניע נמצא במצב "3", והוא מתקדם שלוש שיניים בכל סיבוב של התוף. לו הגלגל היה מוזח ימינה או שמאלה, המספר היה משתנה בהתאם למיקום. על ציר הגלגל המניע יש גלגל שיניים נוסף (לא בתמונה), שמעביר את התנועה לגלגל המתאים בצובר התוצאה.
-
מנגנון האריתמומטר של תומא מ-1822. התמונה צולמה מצידה התחתון של המכונה, אחרי שהכיסוי הוסר. זהו אבטיפוס, עם שלוש ספרות קלט בלבד. המכונה הונעה בעזרת משיכת סרט, שמאוחר יותר הוחלף בארכובה. ניתן לראות את שלושת תופי הפסיעות, ומעליהם את העגלה, במבט מאחור.
-
סכימה של לייבניץ למנגנון גלגל פינים. לייבניץ כנראה המציא את המנגנון, אך אין עדות שבנה או ניסה לבנות מכונה המבוססת על מנגנון זה.
-
שרטוט של גלגל פינים במכונת חישוב מטיפוס "אודהנר". למעשה מדובר בשני גלגלים קונצנטריים. בגלגל הגדול יש 9 פינים רדיאליים, שיכולים לנוע פנימה והחוצה. בגלגל הפנימי יש מסילה מדורגת. שמובילה "מוליך", בכל פין, כך שהמצב היחסי של שני הגלגלים קובע כמה פינים יבלטו. לפני תחילת פעולת החישוב הגלגלים ננעלים זה לזה. בנוסף לגלגל הפינים עצמו, השרטוט מראה מימין גלגלי שיניים נוספים המעבירים את התנועה לספרת התוצאה המתאימה.
-
מכונת חישוב (מטיפוס "אודהנר") של Walther. העגלה בחזית המכונה, מתחת לגוף. בעגלה צובר התוצאה, בן 16 ספרות, ומימינו מונה עם 8 ספרות. בחלק הקבוע צובר הקלט, בן עשר ספרות, מוזן על ידי מנופים שנעים על היקף גליל. כשהערך כרגע בקלט מוצג מעליהם. הארכובה עם הידית השחורה, בצד ימין, מבצעת את הפעולה. בורר הפעולה (חיבור או חיסור) נמצא בחלק העליון של הגוף, משמאל. הידית האדומה השמנה בצד ימין של העגלה משמשת לאיפוס התוצאה, המונה, או שניהם. הכפתורים הלבנים ליד הארכובה משמשים להזחה ספרה אחת ימינה או שמאלה.
-
המונה בעגלה של מכונת חישוב Walther. בתמונה זו הכיסוי ובו החלונות דרכם קוראים את התוצאה הוסר, וניתן לראות את גלגלי הספרות. מימין למונה חלקו השמאלי של צובר התוצאה.
-
מרצדס אויקליד, מ-1937. מכונות מרצדס אויקליד מונעות באמצעות מנגנון "פסי שיניים יחסיים", של קרישטל המאן.
-
מכונת "המאן מאנוס R", של חברת דה-טה-ווה, לפי תכנון של כרישטל המאן. מכונה זו מונעת באמצעות מנגנון "גלגל רצ'ט", ויש לה מספר תכונות מעניינות: מצב ביניים ("חצי פסיעה") מקביל לכל מצב הזחה של העגלה, ומשמש לחיסור • חילוק אוטומטי • העברה לאחור. המכונה יוצרה גם בדגמים ממונעים
-
מרצ'נט פיגורמטיק, יוצרה בין 1950 ל-1952. מנגנון התמסורת הרציפה של המהנדס הרולד איברי, הניע מכונה מהירה יותר ורועשת פחות מכל מכונה אחרת. הכפל מתבצע בעזרת שורת המקשים מימין ללוח הבקרה: אחרי הזנת הנכפל בלוח המקשים המלא, המפעיל מכין את המכונה לביצוע כפל, ואז מזין את ספרות הכופל זו אחר זו בעזרת השורה הימנית. והמכונה מבצעת את הפעולה תוך כדי ההזנה, כך שבסיום הזנת הכופל, צובר התוצאה כבר מראה את המכפלה.
-
מכונת חישוב של פרידן, בערך מ-1962. המכונה מונעת באמצעות וריאציה של תוף פסיעות. לוח המקשים הקטן בצד שמאל משמש להזנת הכופל. זו אחת המכונות הבודדות שמסוגלות לבצע באופן אוטומטי הוצאת שורש והעלאה בחזקה.
-
מחשבון קורטה. מכונה זו מבוססת על ווריאציה של תוף הפסיעות: סידור הקלט והתוצאה על היקף מעגל, מאפשר למכונה להשתמש בתוף יחיד, במקום הסידור הסטנדרטי של תוף נפרד עבור כל ספרה. בתפקיד ה"עגלה" משמש הגליל המחורץ העליון (בתמונה – הגליל עליו מונח אגודלו של המפעיל), ופעולת ההזחה מבוצעת על ידי משיכת העגלה כלפי מעלה, כנגד קפיץ, וסיבובה למצב ההזחה הרצוי. מעבר למצב חיסור נעשה על ידי משיכת הארכובה כדי 3 מ"מ החוצה. זוהי מכונת החישוב המכנית היחידה שראויה לכינוי "מחשבון כיס".
-
מכונת חישוב מסוג "עשר ספרות", Bohn CONTEX 55
תכונות נוספות[עריכת קוד מקור | עריכה]
המנגנונים והתכונות שתוארו לעיל קיימים למעשה בכל מכונות החישוב של ארבע פעולות מאז האריתמומטר. עם השנים, יצרנים שונים הוסיפו תכונות נוספות, ובחלק מהמקרים יצרנים אחרים אימצו תכונות אלו. הרשימה הזו אינה ממצה, אבל מנסה לתאר את התכונות הנפוצות יותר, לצד התכונות המעניינות יותר.
- תצוגת הקלט
- במכונות המוקדמות, כמו האריתמומטר של תומא, האריתמומטר של אודהנר, והמכונות המוקדמות של ברונשוויגה, אין תצוגה נפרדת לקלט, והמפעיל מפעיל רואה את הקלט דרך מיקום המנופים של הספרות השונות. יצרנים הוסיפו שורת ספרות המייצגת את הקלט, לנוחות המפעיל וצמצום טעויות מפעיל.
-
מכונה מוקדמת של ברונשוויגה, ללא תצוגת קלט: המפעיל קורא את ערך הקלט ממיקום המנופים
-
מכונה מתקדמת יותר של אותו יצרן (ברונשוויגה), במכונה זו, הקלט מוצג בשורת הספרות מתחת למנופים (מעל המנופים מופיע מונה הסיבובים)
- מנגנון נשא במונה הסיבובים
- כדי לבצע את הפעולות באופן שתואר למעלה, אין צורך במנגנון נשא עבור מונה הסיבובים: הספרה המתאימה להזחה במונה הסיבובים מקודמת ב-1 בכל סיבוב של הארכובה, ושום פעולה לא דורשת יותר מ-9 פעולות במצב הזחה נתון. במכונות המוקדמות אכן לא היה מנגנון נשא במונה הסיבובים. הוספת מנגנון כזה, מאפשרת קיצורי דרך ופעולות מתקדמות יותר: דוגמה הלקוחה מספר ההפעלה של הקורטה מדגימה זאת: כדי לכפול ב-189, אפשר להשתמש ב"כפל מקוצר": במקום לסובב את הארכובה 9 פעמים עבור היחידות, עוד 8 עבור העשרות, ועוד סיבוב יחיד עבור המאות, המפעיל מבצע פעולת חיסור יחידה עבור היחידות, ועוד אחת עבור העשרות, ואז מבצע שתי פעולות חיבור עבור המאות: כלומר במקום (9x1 + 8x10 + 1x100), המספר 189 מיוצג על ידי (2x100 - 1x10 - 1x1), או 200-11. באופן זה הפעולה מתקצרת מ-18 סיבובים של הארכובה ל-4 סיבובים בלבד. ניסיון לביצוע הפעולה במכונה ללא מנגנון נשא במונה הסיבובים, יביא לכך שבסיום הפעולה המונה לא יראה 189 כפי שהיינו מצפים, אלא 211, כששתי הספרות האחרונות מופיעות באדום, לציון חיסור.
- העברה לאחור
- בחישובים מסובכים יותר מאשר חיבור פשוט, או כפל של שני מספרים, יש צורך להשתמש בתוצאה של החישוב הקודם כקלט לחישוב הבא: למשל, כדי לכפול שלושה מספרים, יש להזין את מכפלת שני המספרים הראשונים כקלט למכפלה השנייה. במקרים אלו, המפעיל נדרש, בתום החישוב, להזין את התוצאה כקלט לחישוב הבא. ה"העברה לאחור" מבצעת את הפעולה הזו באופן מכני, בדרך כלל כחלק מפעולת איפוס התוצאה. בדרך כלל "העברה לאחור" היא מצובר התוצאה לצובר הקלט, אך במכונות מסוימות, ניתן לבחור להעביר לאחור גם את מונה הסיבובים – פעולה נדירה יותר, אך לפעמים שימושית.
- צובר תוצאה כפול
- בסוגי חישובים מסוימים, נחוצות תוצאות ביניים. צובר תוצאה כפול מאפשר זאת. לדוגמה, נניח שהחישוב שמבצעים הוא סכום של מכפלות: ( a*b + c*d +e*f). אם נחוצה התוצאה הכללית בלבד, ניתן פשוט לבצע את שלוש פעולות הכפל זו אחר זו בלי לאפס את התוצאה ביניהן. חישוב כזה ייתן את התוצאה, אבל לא את מכפלות הביניים (למשל e*f). אם אלו נחוצות, יש לבצע את שלוש פעולות הכפל זו אחר זו, כשכל פעם רושמים את התוצאה, ולבסוף חיבור המכפלות (כשהמפעיל נדרש להזין ידנית את תוצאות החישובים הקודמים). בעזרת צובר תוצאה כפול ניתן לבצע את הפעולה בצורה קלה יותר: מבצעים את המכפלה הראשונה, ורושמים את התוצאה. מאפסים את צובר התוצאה הראשון אבל לא את השני, ומבצעים את המכפלה השנייה: עכשיו צובר התוצאה הראשון מראה את המכפלה השנייה, וצובר התוצאה השני את סכום שתי המכפלות. חוזרים על הפעולה עבור כל אחת מהמכפלות (כלומר איפוס הצובר הראשון לפני כל מכפלה נוספת).
- היפוך מונה הסיבובים
- בפעולה רגילה, הספרה המתאימה למצב ההזחה במונה הסיבובים מקודמת ב-1 עבור פעולת חיבור, ומוסגת 1 אחורנית בפעולת חיסור. בפעולות מסוימות, דוגמת חילוק, רצויה התנהגות הפוכה, כלומר קידום ב-1 בחיסור, והסגה של 1 בחיבור. הפיכת מונה הסיבובים, אם התכונה נתמכת, מבוצעת בעזרת מנוף ספציפי השולט על ההפיכה (למשל בקורטה), או באופן אוטומטי, לפי הפעולה שהוזנה בלוח הבקרה.
- חילוק אוטומטי
- מארבע פעולות החשבון הבסיסיות, פעולת החילוק היא המסובכת ביותר, וזו הדורשת את המיומנות הרבה ביותר מהמפעיל. החל מהעשור השני של המאה העשרים הופיעו מכונות חישוב שהציעו חילוק אוטומטי: המפעיל מזין את המחולק (כלומר המונה) בצובר התוצאה, ואת המחלק (המכנה) בצובר הקלט, ואז מבצע את הפעולה (על ידי לחיצה על כפתור החילוק במכונות מונעות במנוע חשמלי, או על ידי סיבוב חוזר של הארכובה במכונה ידנית), ומנגנונים מכניים במכונה מבצעים את כל הפעולות הנחוצות – מעבר בין חיבור וחיסור, והזחת העגלה, עד לסיום הפעולה. המכונות הראשונות שהציעו חילוק אוטומטי היו מכונות מרצדס אויקליד, ובמהרה יצרנים נוספים הציעו תכונה זו. חברת אגלי השווייצרית (יצרנית מכונת הכפל הישיר "מיליונר"), הציעה קו מכונות בשם "מדאס" (MADAS), שהציעו חילוק אוטומטי, החל ב-1913 – השם מדאס הוא ראשי תיבות של "כפל, חילוק אוטומטי, חיבור וחיסור" (Multiplication, Automatic Division, Addition, Subtraction)
- כפל אוטומטי
- כבר ב-1893 הופיעה מכונת החישוב "מיליונר", שביצעה כפל אוטומטי. מכונה זו הייתה גדולה וכבדה (מעל 30 ק"ג), ויקרה, ופעולות חיבור, חיסור וחילוק פחות נוחות לביצוע בה מאשר במכונות חישוב פשוטות יותר. כפל אוטומטי במכונות אחרות הופיע מאוחר יותר, באופן פרדוקסלי אחרי חילוק אוטומטי. בדרך כלל כפל אוטומטי דורש מנגנון קלט נפרד, שמשמש להזנת הכופל, בנוסף לקלט הרגיל דרכו מוזן הנכפל. חלק מהמכונות התומכות בכפל אוטומטי מבצעות את הכפל תוך כדי הזנת הכופל, ובמכונות אחרות הכופל מוזן לפני הפעולה, והמכונה מבצעת את הכפל בשלב נפרד.
-
ב"מיליונר" הזנת הנכפל מתבצעת בעזרת המחלקים בחלק המרכזי (דגמים מאוחרים יותר החליפו את המחלקים בלוח מקשים), והזנת הכופל מתבצעת בעזרת המנוף בצד שמאל, ספר אחרי ספרה, כשהמפעיל מסובב את הארכובה סיבוב אחד אחרי כל ספרה
-
מרצ'נט. הנכפל מוזן דרך לוח המקשים המלא, הכופל דרך שורת המקשים מימין ללוח הבקרה. המפעיל מזין את הכופל ספרה אחרי ספרה, והמכונה מבצעת את הכפל וההזחה אוטומטית, אחרי שהמקש נלחץ
-
פרידן. גם כאן הנכפל מוזן בלוח המקשים המלא, אך הכופל מוזן בעזרת לוח המקשים של 10 ספרות בצד שמאל. הכופל מוזן במלואו לפני ביצוע פעולת הכפל.
-
סלטרון. במכונה זו לוח המקשים המלא כפול ברוחבו מרוב המכונות הדומות – 20 טורים בלוח הספרות.
לביצוע כפל, המפעיל מזין את הנכפל במחצית השמאלית של לוח המקשים, ואת הכופל במחצית השמאלית. -
מכונת חישוב של החברה השוודית פסיט (FACIT). במכונה זו לוח מקשים יחיד של 10 ספרות, המשמש להזנת הנכפל והכופל. במכונה זו, לוח המקשים בתצורה המכונה "דלטון", שהופיעה לראשונה במכונות חיבור אמריקאיות ב-1902. מכונות מאוחרות יותר, של פסיט ויצרנים אחרים, השתמשו בתצורה המוכרת לנו ממחשבונים בני ימינו.
-
מכונת חישוב אלקטרונית מוקדמת של חברת שארפ היפנית, מסביבות 1970. שארפ ייצרה מכונות דומות שנמכרו גם תחת שמות יצרנים אחרים, בדרך כלל יצרני מכונות חישוב מכניות
- שורש ריבועי
- רק דגמים ספורים של יצרן אחד (פרידן, האמריקאי. המכונה מבוססת על תוף פסיעות) מכילים מנגנון הממש אלגוריתם לקירוב שורש ריבועי בעזרת חזרה על סדרת קירובים.
אתגרים[עריכת קוד מקור | עריכה]
קטע מהרצאה של פלט בפני קהל אקדמי ב-1916
|
|---|
|
חזרה לתרגום
' מאת Dorr Felt (ממציא ויצרן הקומפטומטר) "אשמתו של המכונאי"
ארל סטנהוף (צ'ארלס סטנהוף, 1753 − 1813. הדוכס השלישי של סטנהוף, מדינאי, מדען וממציא. בנה דגמים של מכונות חישוב במאה ה-18) היה עוד אחד שהמכונה שלו נבנתה על ידי שען, וגם הוא תלה את חוסר ההצלחה של המכונה בשען שבנה אותה. הוא כנראה צדק – אין ספק שכל העניין מונח על כתפי המכונאי, בונה המכונה. גם השבח וגם האשמה מגיעים למכונאי. כל אחד יכול להגות במוחו מכונת חישוב, אחרי לימוד קצר של הנושא. זו לא בעיה בכלל. קל לתכנן משהו באוויר או על נייר. חשבתי על זה כל הלילה, ובמהרה אמרתי: "אני יכול לבנות מכונה כזו". היה לי ידיד מהנדס חשמל, ואמרתי לו: "תוך 90 ימים, כל משרד בארצות הברית יבצע את כל החישובים באופן מכני". |
קטע מהרצאה של פלט בפני קהל אקדמי ב-1916
|
|---|
|
מאת Dorr Felt (ממציא ויצרן הקומפטומטר) "The Fault of the Mechanic"
Earl Stanhope was another fellow who had his machines made by watchmakers, and he also blames the lack of success to the men who made the machines. I guess he is right. There is no doubt it was the fault of the mechanic. The whole thing rests with the mechanic. He deserves all credit and all blame. Anybody, with a little bit of study, can think up a calculating machine; it is no trouble at all. There are any number of ways to go about it, and devise something in the air or on paper; but it is a very difficult proposition to make one that will be simple and produce accurate results in use. There is hardly a week that I don't get a letter from some man who has invented a calculating machine far superior to anything now on the market, and he wants me to give him the money to patent it, and if I don't, he says he will take all the calculating-machine business away from all the rest of us. It looks simple. When I first thought of making a calculating machine, I was working in a machine shop. I was running a planer. A planer has a tool that runs back and forth across one or more notches according to how you adjust it. I said, "Why can't that be used for counting?" I thought about it all night, and pretty soon I said, "I will make such a machine." I had a friend who was an electrical engineer, and I told him what I was going to do, and said : "In ninety days every office in the United States will be doing its calculating by machinery." So I went to the grocery and bought a macaroni box to make the frame of. I went to the butcher and bought skewers to make the keys of, and to the hardware store and bought staples, and to the bookstore and bought rubber bands to use for springs. I went to work to make a calculating machine, expecting to have thousands in use in ninety days. I began on Thanksgiving Day, because that was a holiday, and worked that day, and Christmas and New Year's, but I didn't get it done in three days. It was a long time before I got it done[11].' "אשמתו של המכונאי"
ארל סטנהוף (צ'ארלס סטנהוף, 1753 − 1813. הדוכס השלישי של סטנהוף, מדינאי, מדען וממציא. בנה דגמים של מכונות חישוב במאה ה-18) היה עוד אחד שהמכונה שלו נבנתה על ידי שען, וגם הוא תלה את חוסר ההצלחה של המכונה בשען שבנה אותה. הוא כנראה צדק – אין ספק שכל העניין מונח על כתפי המכונאי, בונה המכונה. גם השבח וגם האשמה מגיעים למכונאי. כל אחד יכול להגות במוחו מכונת חישוב, אחרי לימוד קצר של הנושא. זו לא בעיה בכלל. קל לתכנן משהו באוויר או על נייר. חשבתי על זה כל הלילה, ובמהרה אמרתי: "אני יכול לבנות מכונה כזו". היה לי ידיד מהנדס חשמל, ואמרתי לו: "תוך 90 ימים, כל משרד בארצות הברית יבצע את כל החישובים באופן מכני". |
ב-1916, דור פלט, ממציא הקומפטומטר, נשא הרצאה בפני קהל אקדמי, ובה תיאר סיור שערך באירופה, ובו ניתנה לו הזדמנות לבחון את מכונות החישוב של פסקל ושל לייבניץ, את האריתמומטר, ומכונות חישוב נוספות, הן עתיקות והן מודרניות.
לדברי פלט, רוב המכונות שבחן חסרות ערך מעשי: זה כנראה נכון עבור כל המכונות שנוצרו לפני האריתמומטר, כמו גם לדגמים המוקדמים יותר של האריתמומטר עצמו (פחות או יותר כל הדגמים והמכונות שיוצרו מאז הדגם הראשון ב-1820, ועד הדגם בתכנון המתקדם של 1862). לפלט הייתה ביקורת קשה על כל המכונות, ולמעשה, לדבריו, המכונה האירופית האמינה היחידה היא המכונה של טייט (טייט היה סוכן מכירות של לייטון, היצרן הבריטי הראשון שייצר "תואמי אריתמומטר". מאוחר יותר החל טייט לייצר בעצמו מכונות עם אותו תכנון בסיסי, אבל עם הרבה שיפורים גדולים וקטנים, שפתרו בעיות שונות, חלקן יתוארו להלן). פלט חשב שכל המכונות האירופיות האחרות שראה לא זכאיות לתואר "מכונת חישוב", משום שהן יכולות, בתנאים מסוימים, לייצר תוצאות שגויות.
מובן שמכונת חישוב, שמדי פעם מוציאה תוצאה שגויה אינה שימושית, אפילו אם התוצאות השגויות נדירות.
נשא
אחד האתגרים הראשונים הוא בניית מנגנון נשא אמין. ככל הידוע, המכונות של שיקארד ושל לייבניץ לא פתרו את האתגר הזה בהצלחה. הפסקלין מימשה מנגנון נשא עם תכנון יותר סולידי, אבל הדיוק המוגבל של תהליכי הייצור הידניים של המאה ה-17, הביאו למכונות שדרשו כוונון וכיול מתמיד, וכשיצאו מהכיול המדויק יכלו לייצר תוצאות שגויות. למעשה, הדרך לאפס את הפסקלין משמשת בדיקה שמנגנון הנשא לא יצא מכיול. כל חישוב מתחיל באיפוס המכונה, כך שמנגנון הנשא נבדק בתחילת כל פעולה.
נהוג לדבר על ה"אריתמומטר" כאילו זו מכונה אחת, אבל למעשה, בין 1820, השנה בה הוגש הפטנט הראשון על המכונה, ובין 1862, השנה בה התגבש התיכון הסופי (פחות או יותר), והחל ייצור בקנה מידה גדול יותר (מאה עד מאות ספורות של מכונות בשנה), המכונה עברה מספר שינויי תכנון משמעותיים, כשהמנגנון שעבר את המספר הרב ביותר של שינויים, והשינויים המשמעותיים ביותר הוא מנגנון הנשא. לפי סטיבן ג'והנסון, בין 1820 ל-1860, מנגנון הנשא של האריתמומטר שונה באופן משמעותי לא פחות מחמש פעמים, עד שהגיע לצורתו הסופית[12].
מנגנון הנשא מהווה אתגר מכמה סיבות: הראשונה היא שהעברת הנשא לספרה הבאה יכולה לגרום לנשא לספרה שאחריה (כשערך הספרה הבאה הוא כרגע 9), ולספרה שאחרי זו, וכן הלאה. אם ערך התוצאה כרגע הוא 9,999,999, והפעולה היא הוספת 1, הנשא מהספרה הראשונה יגרום לנשא בשש הספרות הבאות, ואם מנגנון הנשא בנוי בצורה פשוטה, נוצר עומס מכני על פעולת החיבור הזו, משום שקידום הספרה הראשונה מ-9 ל-0 מתבצע על ידי שן יחידה בגלגל השיניים המניע.
אתגר נוסף שעומד בפני מנגנון הנשא הוא הצורך לשלוב הנעה משני מקורות שונים: ספרת המאות של התוצאה מקבלת קלט הן מספרת המאות של צובר הקלט, והן מהנשא של ספרת העשרות. שילוב שני מקורות הקלט הללו הוא אתגר מעניין, ומתכננים שונים פתרו אותו בצורות שונות.
עוד אתגר בנשא הוא פעולת החיסור: במכונות חישוב בהן החיסור מתבצע על ידי סיבוב גלגל הספרות של התוצאה בכיוון הפוך (יש מכונות שמבצעות חיסור על ידי חיבור המשלים. במכונות אלו אין הבדל בפעולת הנשא בין חיבור וחיסור), הנשא צריך לעבוד בכיוון הפוך: הנשא מופעל כשהתוצאה עוברת מ-0 ל-9 (במקום מעבר מ-9 ל-0 בחיבור), והפעולה הנדרשת כשיש נשא היא הפוכה – חיסור אחד מהספרה הבאה במקום חיבור. תכנון נשא שיעבוד נכון בחיסור אינו מורכב או מסובך יותר מתכנון נשא שיעבוד בחיבור – האתגר כאן, הוא בניית מנגנון שעובד נכון גם בחיבור וגם בחיסור. יש מכונות בהן חיסור מתבצע על ידי "חיבור המשלים", ובמכונות אלו גם הנשא פועל רק בכיוון אחד. כמה ממכונות אלו הן הפסקלין, קומפטומטר, מרצדס אוקליד, וקורטה.
אתגר נוסף הוא ההנעה: מימוש הנשא נמצא, לפחות בחלקו, בעגלה, והנעתו מהווה אתגר מכני, בין השאר משום שהעגלה לא מקובעת לגוף בנקודה מסוימת, אלא מוזחת ימינה ושמאלה.
הרוב המכריע של מכונות החישוב של ארבע פעולות משתמשות באחד משני סוגי מנגנון הנעה – גלגל פינים או תוף פסיעות (גלגל לייבניץ). במכונות רבות מופיעות וריאציות מגוונות למימוש המנגנון. לעומת זאת, המכונות השונות מממשות מנגנוני נשא רבים ושונים, המבוססים על עקרונות מכניים מגוונים.
רוב המנגנונים פותרים את שני האתגרים הראשונים בעזרת ביצוע הנשא בשני שלבים שונים: בשלב הראשון צובר התוצאה משולב עם מנגנון הקלט שמקדם כל ספרה במידה הנחוצה. כשנוצר נשא (כלומר כאשר ספרה כלשהי מתקדמת מ-9 ל-0), הנשא "מסומן", על ידי פעולה מכנית כלשהי, כמו דחיפת פין, הסטת מנוף, וכדומה. כאשר הזנת הקלט מסתיימת, צובר הקלט מתנתק מהתוצאה, ומנגנון שני "סורק" את סימוני הנשא, ובכל מקום שמסומן נשא, המנגנון מקדם את הספרה הבאה. יש לבצע את הפעולה הזו באופן סדרתי, החל מספרת היחידות ועד הספרה העליונה של התוצאה, משום שחיבור הנשא לספרה הנוכחית יכול לגרום להופעת נשא חדש בספרה הבאה.
במכונות מטיפוס "אודהנר" פותח מנגנון נשא פשוט ואפקטיבי, שהופיע, בווריאציות קלות, בהרבה מכונות מטיפוס זה[13].
הנעת יתר
אתגר נוסף היא תופעת הנעת היתר (overthrow). תיאור פשטני של הבעיה, הוא כדלקמן: כשגלגל השיניים שמניע את גלגל אחר מתנתק, הגלגל המונע ממשיך להסתובב, כתוצאה מההתמד, ונוצרת שגיאה בחישוב. גם כאן, פותחו שיטות רבות ומגוונות להתגבר על האתגר.
סוף הדרך[עריכת קוד מקור | עריכה]
שנות ה-60 של המאה ה-20, היו העשור הטוב ביותר למכונות החישוב, הן מהבחינה הטכנית: המכונות היו אמינות, מהירות, ונוחות להפעלה יותר מאי פעם, והן מהבחינה המסחרית: עסקים, משרדים, חברות, אקדמיות ומשרדי ממשלה הרחיבו את הדרישה למכונות חישוב, והמכירות הגיעו למספרים גדולים יותר מאי פעם, הן במספר היחידות והן בהכנסות כספיות. עשור זה היה גם העשור האחרון: מכונות חישוב אלקטרוניות, ומאוחר יותר מחשבונים, דחקו את גלגלי מכונות החישוב לערימות הגרוטאות ולמוזיאונים.
הסימן הראשון הגיע בתחילת העשור – החברה הבריטית Bell Punch, שפעלה בתחום מכונות החישוב מאז המחצית הראשונה של המאה, וב-1960 רכשה את הזכויות לשם המסחרי ולתכנון של הקומפטומטר, וייצרה ומכרה קומפטומטרים ומכונות חישוב אחרות באירופה, הציגה באוקטובר 1961 את מכונת החישוב האלקטרונית הראשונה: ANITA (אנ').
האניטה בישרה את תחילת הקץ: המכונה עצמה, הייתה מבוססת על שפופרות, ועדיין הציגה ממשק משתמש כמו של מכונת חישוב מכנית עם לוח מקשים מלא, והייתה גדולה, כבדה, ויקרה יותר ממכונות החישוב המכניות. יתרונותיה, השקט והמהירות לא הספיקו כדי שהאניטה עצמה תהווה איום ממשי על תעשיית מכונות החישוב, אבל מכונות החישוב האלקטרוניות שבאו אחריה נפטרו מהחסרונות הללו זה אחרי זה: חברות נוספות, בתחילה יצרניות מכונות חישוב מכניות כמו מונרו, פרידן ו-SCM האמריקאיות, אוליבטי באיטליה, פסיט השוודית, שארפ היפנית ועוד, ומאוחר יותר חברות נוספות שהגיעו מתחומים אחרים, ביניהן Wang ו-HP האמריקאיות, החלו לייצר מכונות חישוב אלקטרוניות, כשטרנזיסטורים, ומאוחר יותר מעגלים משולבים מחליפים את השפופרות, לוח מקשים של 10 ספרות מחליף את לוח המקשים המלא, ותצוגת דיודות פולטות אור (LED), ומאוחר יותר גם תצוגת גביש נוזלי, מחליפות את התצוגות המגושמות מסוג Nixie (אנ') שאפיינו את מכונות החישוב האלקטרוניות הראשונות. מכונות החישוב של Wang ו-HP הוסיפו פונקציונליות שלא קיימת במכונות מכניות, לבצע חישובים "מדעיים" בנוסף לארבע פעולות החשבון: חישובים טריגונומטריים, ולוגריתמיים. המכונות של וואנג ו-HP, וכמה מהמכונות האלקטרוניות האחרות, הציגו גם יכולת תכנות מוגבלת, ותמיכה בנקודה צפה.
רוב המכונות הללו השתמשו בזיכרון ליבה מגנטית, ועשו שימוש בטרנזיסטורים למימוש יחידת החישוב, שהתבססה על טכנולוגיות מתחום המחשבים.
לקראת סוף העשור, חברות אמריקאיות ויפניות פיתחו מעגלים משולבים שאפשרו לבנות מכונת חישוב בעזרת מספר קטן יחסית של רכיבים – כמה עשרות במקום כמה מאות, ומספר חברות יפניות פיתחו מכונות חישוב שנמכרו תחת שמן, ותחת שמות יצרנים אחרים, כמו פסיט השוודית ואחרות. מכונות חישוב אלו דמו בדרך כלל למחשבונים מודרניים בממשק: לוח ספרות בן עשר ספרות, מקשים לפעולות השונות, ותצוגה בסגנון "שבעה סגמנטים" (Seven-segment display).
חברת בוזיקום (Busicom) היפנית, פנתה ב-1970 לשתי חברות אלקטרוניקה אמריקאיות לפיתוח מעגל משולב למכונת חישוב. אחת החברות הללו הייתה אינטל, שהציעה כפתרון פיתוח מעבד זעיר, ובכך עשתה היסטוריה – המעבד, 4004, נחשב בדרך כלל למיקרו-מעבד הראשון בעולם. החברה השנייה הייתה Mostek (אנ'), שפתרה את הבעיה בצורה שונה – היא פיתחה מכונת חישוב על שבב יחיד. הפיתוח ארך זמן רב יותר, אבל היה פתרון טוב יותר עבור מכונת חישוב: מכונת החישוב שהשתמשה במעבד של אינטל הכילה מספר גדול יחסית של שבבים – כדי שהמעבד יוכל לפעול הוא נזקק לשבב זיכרון, שבב זיכרון קריאה בלבד (ROM), ומספר רכיבים נוספים, כמו בקר קלט/פלט. לעומת זאת, השבב הייעודי הצריך הרבה פחות תמיכה היקפית, ואפשר מכונות חישוב קטנות וזולות יותר, ומאוחר יותר מחשבונים. חברות נוספות, ובראשן טקסס אינסטרומנטס (TI), ייצרו שבבים דומים, ובעקבות מלחמת המחירים שהתפתחה, למכונות החישוב המכניות לא היה מה להציע: תוך זמן קצר הופיעו מכונות אלקטרוניות שהיו קטנות, זולות, מהירות, שקטות, ונוחות להפעלה במידה ששום מכונת חישוב מכנית לא יכלה להתחרות בה. בחברות בהן מכונות החישוב המכניות יוצרו במחלקה (כמו בורוז, למשל), המחלקה נסגרה, וחברות בהן מכונות חישוב מכניות היו המוצר העיקרי או היחיד נסגרו.
חברת Facit השוודית (אנ'), שבתחילת 1970 העסיקה מספר שיא של 14,000 עובדים, עם מחזור מכירות שנתי של כמיליארד קרונות[14], הגיעה תוך פחות משנתיים למצב של פיטורים המוניים, ובסוף 1972 יצאה למעשה מתחום מכונות החישוב לחלוטין. ההתמוטטות המהירה של החברה ידועה עד היום בשוודיה כ"כשל פסיט".
יצרנים רבים של מכונות חישוב מכניות פיתחו וייצרו דגמים של מכונות חישוב אלקטרוניות, אבל הן נעלמו למעשה כגורמים משמעותיים בשוק המחשבונים, אחרי מלחמת מחירים אגרסיבית בתחילת שנות ה-70 של המאה ה-20, שצמצמה למעשה גם את שוק "מכונות החישוב" האלקטרוניות, לטובת מחשבונים.
ראו גם[עריכת קוד מקור | עריכה]
קישורים חיצוניים[עריכת קוד מקור | עריכה]
- אבני דרך, עשרת החידושים הבולטים של מדעי המחשב, באתר ifeel
הערות שוליים[עריכת קוד מקור | עריכה]
- ^ K. Kadokura, סטטיסטיקות מכירת מכונות חישוב ומחשבונים ביפן, בין 1962 ל-1970, באתר www.xnumber.com, מאי 2017
- ^ 1 2 3 ארנסט מרטין, תרגום: (מגרמנית לאנגלית) - Peggy Aldrich Kidwell ו-Michael R. Williams, THE CALCULATING MACHINES (DIE RECHENMASCHINEN), The MIT Press Cambridge, Massachusetts London, England
- ^
 How the Arithmometer Works: אנימציה המציגה ומסבירה את אופן פעולת האריתמומטר, סרטון באתר יוטיוב
How the Arithmometer Works: אנימציה המציגה ומסבירה את אופן פעולת האריתמומטר, סרטון באתר יוטיוב
- ^ מרק גלוסקר, The ternary calculating machine of Thomas Fowler
- ^ ג'והן וולף, Felt & Tarrant - The Comptometer, John Wolff's Web Museum
- ^ John Wolff's Web Museum - Millionaire - Technical Description, www.johnwolff.id.au
- ^ John Wolff's Web Museum - Full-function Ten-key Calculators, www.johnwolff.id.au
- ^ Robert W. Seidel, Evolving from calculators to computers, library.sciencemadness.org, 1995
- ^ ג'והן וולף, Register of Millionaire Calculators, John Wolff's Web Museum
- ^ Erhard Anthes, Die Mercedes Euklid 1910-1970 Wandlungen einer Rechenmaschine (ארכיון)
- ^ Mechanical arithmetic, or The history of the counting machine, archive.org
- ^ Stephen Johnston, Making the arithmometer count, www.mhs.ox.ac.uk (באנגלית)
- ^ John Wolff's Web Museum - Original-Odhner - Technical Description, www.johnwolff.id.au
- ^ מיליארד קרונות שוודיות ב-1970 שווה ערך בערך ל-200 מיליון דולר אמריקאי ב-1970, או 1.7 מיליארד דולר ב-2015



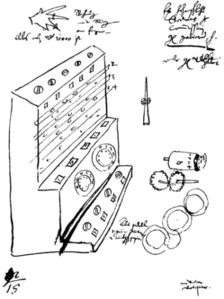



![מכונת חישוב של האן ב-Württemberg State Museum, שטוטגרט. האן וגיסו שוסטר בנו כתריסר או יותר מכונות חישוב לפי התיכון הזה, בין 1774 ו-1820[2].](http://upload.wikimedia.org/wikipedia/commons/thumb/9/95/Rechenmaschine_Philipp_Matth%C3%A4us_Hahn_%282%29.jpg/346px-Rechenmaschine_Philipp_Matth%C3%A4us_Hahn_%282%29.jpg)