מומנט התמד

במכניקה של גוף קשיח, מומנט ההתמד של מסה (ידוע גם בשמות מומנט אינרציה, או מסה זוויתית) מתאר את היחס בין מומנט הכוח המופעל על הגוף לבין התאוצה הזוויתית שאותה יפתח הגוף סביב ציר הסיבוב. בהקבלה לתנועה קווית, שם המסה מהווה את היחס בין הכוח הפועל על הגוף לתאוצת הגוף ובעצם מתארת את רמת ההתנגדות של הגוף אל השינוי בתנועה, כך גם בתנועה זוויתית של גוף קשיח (סיבוב סביב צירו) מומנט ההתמד מתאר את רמת ההתנגדות של הגוף לשינוי בתנועה הזוויתית.

מומנט ההתמד הוא תכונה של גוף עבור ציר סיבוב מסוים - אין משמעות לביטוי "מומנט ההתמד של הגוף" ללא ציון הציר סביבו הוא מחושב או נמדד. ציר הסיבוב יכול לעבור בתוך הגוף ויכול לעבור מחוצה לו, אך לרוב נוח לחשב סביב הצירים הראשיים של הגוף, שעוברים במרכז המסה שלו. בשביל תמונה מלאה של מומנט ההתמד סביב צירים אלה, לא מספיק סקלר, ונזדקק לטנזור התמד. לאחר החישוב סביב הצירים הראשיים, ישנה דרך פשוטה לחישוב מהיר סביב צירים אחרים מקבילים, בשם משפט שטיינר-הויגנס.

הגדרה מתמטית

כדי להגדיר לגוף את מומנט האינרציה שלו, נצטרך תחילה לבחור ציר סיבוב סביבו הוא נע. בתוך הציר הזה נבחר את נקודת ראשית הצירים על מנת לחשב ממנה את כל המרחקים. בחירת הנקודה המדויקת איננה משפיעה על התוצאות כל עוד היא על ציר הסיבוב.

עבור חלקיק נקודתי, נחשב את מומנט האינרציה בהתאם להגדרתו כיחס בין המומנט לתאוצה הזוויתית:

${\vec {\tau }}={\vec {r}}\times {\vec {F}}={\vec {r}}\times m{\vec {a}}=m{\vec {r}}\times \left({\vec {\alpha }}\times {\vec {r}}\right)=m||{\vec {r}}_{\perp }||^{2}\alpha$

כאשר משתי המכפלות הווקטוריות יצא שצריך להשמיט את החלק המקביל לציר הסיבוב ולכן נשאר לנו רק החלק המאונך (כי התאוצה הזוויתית מאונכת לציר הסיבוב). לפי זה אין משמעות לנקודת הראשית שבחרנו אלא רק למרחק מהציר. מה שאומר שאם נסמן $r=||{\vec {r}}_{\perp }||$, נקבל: $I=mr^{2}$

כעת נתבונן על נקודה אינפיניטסימלית בגוף הקשיח, יש לה מסה $dm$ ומרחק $r$ מציר הסיבוב. נוכל לסכום על כל הנקודות שבתוך הגוף ולהגיע למומנט האינרציה של כלל הגוף.

$I\ {\stackrel {\mathrm {def} }{=}}\ \int _{m}r^{2}\,dm=\int _{V}r^{2}(V)\,\rho (V)\,dV=\iiint _{V}r^{2}(x,y,z)\,\rho (x,y,z)\,dx\,dy\,dz\!$

כאשר:

• $\ V$ - הוא נפח הגוף
• $\ r$ - הוא המרחק של יחידת מסה מציר הסיבוב
• $\ m$ - היא מסת הגוף
• $\ \rho$ - הוא פונקציית הצפיפות של הגוף
• $\ x,y,z$ - הן הקואורדינטות של יחידת מסה של הגוף במערכת צירים קרטזית

במקרה הבדיד (מספר סופי של חלקיקים נקודתיים בעלי מסה מוגדרת לכל אחד) ניתן להשתמש בנוסחה:

$\ I=\sum _{i}^{N}m_{i}r_{i}^{2}$

הסבר אינטואיטיבי ודוגמאות להמחשה

ניתן להבין את המשמעות הפיזיקלית של מומנט ההתמד דרך מספר תופעות יומיומיות המדגימות כיצד מסת הגוף ופיזורה במרחב משפיעים על תנועתו הסיבובית:

• כדי להתחיל לסובב כדור כדורסל על קצה האצבע נדרש מאמץ קטן יחסית. לעומת זאת, כדי לסובב כדור באולינג באותו הגודל ובאותה מהירות, נדרש כוח סיבובי (מומנט) גדול בהרבה. הסיבה לכך היא המסה הגדולה של כדור הבאולינג, המגדילה את מומנט ההתמד שלו וגורמת לו "להתנגד" יותר לשינוי במצבו הסיבובי. באותו אופן, הרבה יותר קשה לעצור כדור באולינג שכבר מסתובב מאשר לעצור כדורסל מסתובב.

• מומנט ההתמד תלוי לא רק במסה, אלא בעיקר במרחקה מהציר. אם ניקח מוט ונצמיד שתי משקולות למרכזו, יהיה קל מאוד לסובב אותו מצד לצד סביב המרכז. אך אם נזיז את אותן משקולות לקצות המוט, נגלה שקשה הרבה יותר להתחיל או להפסיק את הסיבוב. למרות שהמסה הכוללת לא השתנתה, העובדה שהיא רחוקה יותר מהציר מגדילה את מומנט ההתמד "בריבוע המרחק"

• לוליין ההולך על חבל דק מחזיק בדרך כלל מוט ארוך מאוד. המוט מגדיל משמעותית את מומנט ההתמד של הלוליין ביחס לציר הנפילה שלו. אם הלוליין מתחיל לאבד שיווי משקל ולנטות הצידה, מומנט ההתמד הגדול של המוט "מתנגד" לסיבוב הנפילה ומאט אותו. האטה זו מעניקה ללוליין זמן יקר לתיקון היציבה לפני שיפול.
• הדוגמה הקלאסית לשינוי מומנט התמד היא רקדנית בלט או מחליקה אמנותית המבצעת סחרור (פירואט). כאשר הרקדנית מצמידה את ידיה לגופה, היא מקטינה את פיזור המסה סביב ציר הסיבוב ובכך מקטינה את מומנט ההתמד שלה. לפי חוק שימור תנע זוויתי (המתואר בפירוט בהמשך), התנע הזוויתי נשמר כל עוד לא פועל מומנט חיצוני. לכן, הקטנת מומנט ההתמד גוררת עלייה מיידית במהירות הזוויתית, כדי לשמור על ערכו של התנע. כלומר, הרקדנית מסתובבת מהר כתוצאה מקירוב הידיים לגופה. מנגד, פרישת הידיים לצדדים תגדיל את מומנט ההתמד ותגרום להאטה במהירות הסיבוב.
• ישנן מכוניות צעצוע בהן מותקן גלגל מתכת כבד (גלגל תנופה). גלגל זה הוא בעל מומנט התמד גדול (יחסית) ולאחר שמתחילים להסיע את המכונית הוא מתחיל להסתובב וכשעוזבים אותה הוא ממשיך להניע. מומנט ההתמד הגבוה שלו מונע ממנו להאט במהירות (האטה שנגרמת תמיד בגלל כוח החיכוך) וכך המכונית ממשיכה לנסוע.

את הקריטריונים של גודל המסה, ההתפלגות שלה ושימור התנע הזוויתי ניתן לראות מתוך ההגדרות.

הסבר איכותי ושימושים

השימוש הבסיסי ביותר במומנט התמד הוא:

$\ \sum {\vec {\tau }}=I\ {\vec {\alpha }}$

כאשר:

• ${\vec {\alpha }}$ - התאוצה הזוויתית של גוף (שקולה לתאוצה קווית בתנועה בקו ישר)
• $\ I$ - מומנט ההתמד של הגוף שהוא גודל סקלרי, לא וקטור (במקרה הפשוט $\ I=mr^{2}$ ובעצם שקול למסה של הגוף בתנועה בקו ישר)
• ${\vec {\tau }}$ - מומנט הכוח. (שקול לכוח בתנועה בקו ישר)

ולכן נוסחת המומנט בתנועה מעגלית שקולה לחוק השני של ניוטון בתנועה בקו ישר: $\ \sum {\vec {F}}=m\ {\vec {a}}$. מכאן רואים שככל שנפעיל מומנט כוח גדול יותר על הגוף כך נקבל תאוצה זוויתית גדולה יותר. תאוצה זוויתית זו תתקבל ביחס ישר כאשר I הוא קבוע היחס.

בכמה מובנים נוספים, מומנט ההתמד משמש כמקבילה הזוויתית למסה, ודרכו אפשר לחשב גדלים רבים:

גודל	תנועה קווית	תנועה זוויתית
החוק השני של ניוטון	${\vec {F}}=m{\vec {a}}$	${\vec {\tau }}=I{\vec {\alpha }}$
תנע	${\vec {P}}=m{\vec {v}}$	${\vec {L}}=I{\vec {\omega }}$
אנרגיה קינטית	$E_{K}={\frac {mv^{2}}{2}}$	$E_{K}={\frac {I\omega ^{2}}{2}}$

חישוב מומנט התמד של גוף מורכב

עבור חישוב מומנט התמד של גוף כללי ("מסובך") המורכב ממספר גופים נדרש לבצע:

• חישוב מומנט ההתמד של כל אחת מן המסות אשר מרכיבות את הגוף סביב הציר בו הגוף מסתובב
  • במקרה של מסה לא נקודתית המרכיבה את הגוף (מלבן, עיגול) נחשב את מומנט ההתמד שלה סביב הציר הרצוי בעזרת משפט שטיינר
• נבצע חיבור של כל מומנטי ההתמד ונקבל את מומנט ההתמד השקול של הגוף הכללי

סכום מומנטי ההתמד

סכום מומנטי ההתמד למערכת צירים ישרת זווית איננו מושפע מהכוון של הצירים אלא רק ממיקום מוצא הצירים.

$\ I_{xx}+I_{yy}+I_{zz}=\iiint _{V}(y_{i}^{2}+z_{i}^{2})\,\rho (v)\,dv+\iiint _{V}(x_{i}^{2}+z_{i}^{2})\,\rho (v)\,dv+\iiint _{V}(x_{i}^{2}+y_{i}^{2})\,\rho (v)\,dv\!$

$\ I_{xx}+I_{yy}+I_{zz}=\iiint _{V}2(x_{i}^{2}+y_{i}^{2}+z_{i}^{2})\,\rho (v)\,dv=\iiint _{V}2r^{2}\,\rho (v)\,dv\!$

כאשר:

• $\ V$ - הוא נפח הגוף
• $\ r$ - הוא המרחק של יחידת מסה מראשית הצירים
• $\ \rho$ - הוא פונקציית הצפיפות של הגוף
• $\ x,y,z$ - הן הקואורדינטות של יחידת מסה של הגוף במערכת צירים קרטזית

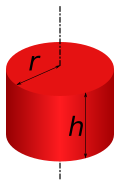
מומנטי התמד של גופים שונים, סביב ציר הסיבוב

	${\frac {1}{2}}Mr^{2}$		${\frac {1}{12}}Ml^{2}$
	${\frac {1}{12}}M(a^{2}+b^{2})$		${\frac {2}{5}}Mr^{2}$		${\frac {1}{2}}M({r_{2}}^{2}+{r_{1}}^{2})$

כאשר:

• $\ M$ - היא מסת הגוף
• $\ r$ - הוא רדיוס הגליל או הכדור ביחידות אורך
• $\ h$ - הוא גובה הגליל ביחידות אורך
• $\ a,b$ - הם ממדי התיבה ביחידות אורך
• $\ l$ - הוא אורך הגליל ביחידות אורך

ראו גם

• טנזור התמד
• משפט שטיינר
• מומנט ההתמד של השטח
• מומנט התמד פולרי של השטח
• מומנט התמד פולרי מנורמל

לקריאה נוספת

• Sybil P. Parker, McGraw Hill Encyclopedia of Engineering, 1983.
• McGraw-Hill Dictionary of Scientific and Technical Terms, 6th ed. by The McGraw-Hill Companies, 2003
• Irving H. Shames, Engineering Mechanics, Prentic - Hill International Inc. 1970

קישורים חיצוניים

מדיה וקבצים בנושא מומנט התמד בוויקישיתוף

• ד"ר אבי סאייג, חולה על כדורגל, באתר של מכון דוידסון לחינוך מדעי, 26 ביוני 2018
• מומנטי אינרציה לגופים שונים, באנגלית
• מומנט האינרציה של המסה, באנגלית efanda.
• מומנט האינרציה, באנגלית
• מומנט התמד, באתר אנציקלופדיה בריטניקה (באנגלית)
• מומנט התמד, באתר MathWorld (באנגלית)

---