משפט וולף וצורת גביש בשיווי משקל

משפט וולף (Wulff theorem), על שם הקריסטלוגרף הרוסי גיאורג וולף , קובע את הצורה של גביש בשיווי משקל (equilibrium crystal shape - ECS). צורה זו ממזערת את האנרגיה החופשית של פני השטח של הגביש בנפח קבוע. לצורך קביעת ה-ECS משתמשים בבניית וולף (Wulff reconstruction).

בניית קירי

בניית קירי לתיבה בעלת נפח קבוע ואנרגיה משטחית מינימלית.

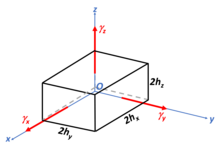
ג'וסיה וילארד גיבס טען במאמר מ-1876, שטיפה או גביש יסדרו את עצמם כך שהאנרגיה החופשית של גיבס שלהם תמוזער על ידי קבלת צורה כזו שלפני השטח שלה יש את האנרגיה החופשית המזערית: ${\mathcal {G}}_{s}=\sum _{i}\gamma _{i}A_{i}$. כאן ${\mathcal {G}}_{s}$ היא האנרגיה החופשית המשטחית של הגוף (טיפה או גביש), $\gamma _{i}$ - האנרגיה החופשית הספיציפית (כלומר ליחידת שטח, במילים אחרות: מתח הפנים) של המשטח ה-i של הגוף, ו-$A_{i}$ השטח של המשטח ה-i הזה. בשנת 1885 פרסם פייר קירי מאמר, שבו הרחיב את קביעתו זו של גיבס. במאמרו, פתר קירי את הבעיה של הצורה של גבישים עבור מנסרה ריבועית ועבור קובוקטהדרון. נְפַתֵּחַ כאן את הגישה שלו לתיבה שמרכזה בראשית הצירים O, ומרחקי פיאותיה מהראשית הם: $h_{x},h_{y},h_{z}$ (כמוראה באיור). השטחים של פאות התיבה בכיוונים $x,y,z$ הם: $4h_{y}h_{z},4h_{x}h_{z},4h_{x}h_{y}$, בהתאמה; ונפח התיבה: $V=8h_{x}h_{y}h_{z}$. האנרגיה המשטחית של התיבה היא סכום האנרגיות החופשיות של כל הפאות של התיבה: ${\mathcal {G}}_{s}=2\cdot \gamma _{x}4h_{y}h_{z}+2\cdot \gamma _{y}4h_{x}h_{z}+2\cdot \gamma _{z}4h_{x}h_{y}={{\gamma _{x}}V \over h_{x}}+{{\gamma _{y}}V \over h_{y}}+8\gamma _{z}{h_{x}}{h_{y}}$, כשבטאנו בשוויון השני את $h_{z}$ באמצעות $V$ ו-$h_{x}$ ו-$h_{y}$.

כדי למצוא את המרחקים $h_{x}$ ו-$h_{y}$ שיתנו את האנרגיה החופשית המשטחית המינימלית צריך שהנגזרות החלקיות המתאימות תתאפסנה. זה ייתן: $\gamma _{x}{h_{y}}{h_{z}}={\gamma _{y}{h_{x}}{h_{z}}}{=\gamma _{z}{h_{x}}{{h}_{y}}}={Constant}$. כלומר, האנרגיות החופשיות של כל הפאות של הגביש בשיווי משקל שוות זו לזו. יש לשים לב, גם, שהשטחים של הפאות תלויים הפוך במרחקים שלהן ממרכז הגביש (למשל, $h_{x}h_{y}={{V} \over {8}{h_{z}}}$). מרחקים אלו פרופורציונליים, לכן, לאנרגיות החופשיות המשטחיות הספציפיות: ${{\gamma }_{x}/{h}_{x}}={{\gamma }_{y}/{h}_{y}}={{\gamma }_{z}/{h}_{z}}\varpropto {\sqrt[{3}]{\operatorname {} \!{{\gamma }_{x}}\!{{\gamma }_{y}}\!{{\gamma }_{z}} \over \operatorname {} \!V}}$.

במילים אחרות: פנים עם אנרגיה חופשית משטחית חופשית ספציפית גבוהה מצויים רחוק יותר ממרכז הגביש, מאשר אלו עם אנרגיה חופשית משטחית ספציפית נמוכה, לראשונים יש שטח פנים נמוך יותר יחסית.

משפט וולף

על סמך תצפיותיו בגבישים שונים, הכליל ג'ורג' וולף את התוצאות של קירי עבור כל גביש בצורת פוליהדרון: אנרגיית פני השטח המינימלית של פוליהדרון בעל נפח נתון תושג כשהמרחקים של פאות הפליהדרון מנקודה נתונה אחת יהיו פרופורציונליים לאנרגיות המשטחיות הספציפיות של הפאות. כלומר, ${{\gamma }_{i}/{h}_{i}}=Constant$ עבור כל פאה $i$ בפוליהדרון.

בניית וולף

באמצעות בניית וולף אפשר לקבל את צורת שיווי המשקל של גביש (equilibrium crystal shape - ECS). העקום האדום מתאר את האנרגיה החופשית של פני השטח, γ, כפונקציה של הכיוון (אורכו של החץ האדום בכל כיוון פרופורציונלי לגודלה של האנרגיה החופשית המשטחית באותו כיוון). הקווים הכחולים t הם המשיקים לעקום האנרגיה החופשית (ניצבים לקווים החומים המחברים את נקודת ההשקה עם הראשית של עקום האנרגיה החופשית המשטחית). צורת שיווי המשקל של הגביש, המתוארת על ידי העקום הכחול המודגש, היא המעטפת הפנימית של כל המשיקים לעקום γ.

בשנת 1951 הכליל קונירס הרינג ממעבדות בל בניו ג'רזי את משפט וולף לכלל הגופים הקמורים (לאו דווקא פוליהדרונים). הוא פיתח בנייה גיאומטרית לקביעת צורת שיווי המשקל (ECS) של גביש - היא בניית וולף: בשלב ראשון בונים את עקום האנרגיה החופשית הספציפית בכל כיוון, $\gamma (\theta ,\phi )$, בקואורדינטות פולריות. עבור גביש דו-ממדי מותחים מהראשית וקטור בכיוון $\theta$ שאורכו פרופורציונלי לגודלה של האנרגיה המשטחית הספציפית באותו כיוון (החץ האדום באיור). אוסף קצות הווקטורים בכל הכיוונים יוצר את עקום $\gamma (\theta )$ של החומר, הנקרא גם עקום וולף. בשלב שני קובעים גרפית את צורת שיווי המשקל של הגביש (ה-ECS) בצורה הבאה: בכל נקודה על עקום וולף מעבירים משיק, $t$, לעקום (ישרים כחולים באיור), כלומר ניצב לקו הרדיאלי המחבר את הנקודה עם מרכז העקום (הישרים החומים באיור). המעטפת הפנימית של משיקים אלו נותנת את צורת שיווי המשקל (מסומנת בעקום כחול מודגש באיור). אם יש חודים בעקום וולף, הבנייה תיתן צורת שיווי משקל שיש בה פאות מישוריות (הקווים הכחולים הישרים, שניצבים לקווים השחורים באיור). אם פאות אלו לא חותכות זו את זו בתוך עקום וולף, יתקבלו ב-ECS "פינות מעוגלות" (מחוספסות, המכילות מספר רב של מישורי שיווי-משקל), המפרידות בין המישורים הראשיים המרכיבים את צורת הגביש בשיווי-משקל (4 הפינות הכחולות המעוגלות באיור). הצורה של הפינות המעוגלות נקבעת על ידי המעטפת הפנימית של המשיקים לעקום וולף משני העברים של כל "פינה".

בניית הרינג

בגלל האזורים המחוספסים ב-ECS, קביעתה של צורת הגביש בשיווי-משקל מעקום וולף אינה תמיד קלה כל כך. הרינג תיאר במאמרו בנייה נוספת - בניית הרינג - האומרת היכן במרחב האמיתי $(x,y,z)$ יופיע מישור בעל כיוון מסוים. הבנייה מקשרת, אם כן, בין נקודות במרחב האנרגיה-כיוון $(\gamma ,\theta ,\phi )$, ובין נקודות במרחב האמיתי $(x,y,z)$. במקרה זה רוצים לדעת האם הכיוון $P$ מיוצג בגביש בצורת שיווי המשקל שלו בנקודה שכיוונה $Q$? במילים אחרות, האם בכיוון כלשהו $Q$ בגביש קיים, בצורת שיווי-המשקל שלו, מישור כלשהו, שכיוונו $P$, כלומר מישור שניצב לווקטור ${\overrightarrow {OP}}$, היכן ש-$O$ היא הראשית של עקום וולף $\gamma (\theta ,\phi )$ [או $\gamma (\theta )$ בדו-ממד]. זה יהיה המצב אם המישור $PQ$ הוא חלק מהמעטפת הפנימית של המשיקים לעקום וולף $\gamma (\theta )$, כך שאין משיק אחר ל-$\gamma (\theta )$ החותך את הכיוון ${\overrightarrow {OQ}}$ קרוב יותר לראשית.

בניית הרינג להסקה האם המישור שכיוונו P מיוצג בצורת שיווי המשקל של הגביש בנקודה שכיוונה Q. עבור העקום γ(θ) (באדום) ב-א' הכיוון P מיוצג, מפני שבכל הכיוונים (למשל בכיוון R) העקום γ(θ) נמצא מחוץ לכדור המשיק (בחום). לעומת זאת, ב-ב' המישור שכיוונו P, אינו מיוצג, מפני שבכיוון אחר, T, העקום γ(θ) נמצא בתוך הכדור המשיק. צורת שיווי המשקל (ECS) של מקרה א' מוראית בכחול ב-ג', והיא מכילה פינות מעוגלות (מחוספסות). לעומת זאת, ה-ECS של מקרה ב', המוראית ב-ד', מכילה רק מישורים שטוחים ופינות חדות.

הבנייה (ראו איור) מורכבת מציור עיגול שקוטרו עובר בראשית של עקום וולף ($O$) ובנקודה הנדונה $Q$, כך שישיק לעקום וולף, $\gamma (\theta )$ (בדו-ממד), בנקודה $P$. הזווית $\angle OPQ=90^{\circ }$ כי היא נשענת על קוטר, ולכן כיוון המישור $PQ$ הוא ${\overrightarrow {OP}}$ (כלומר, הוא אמנם משיק לעקום וולף).

קריטריון הרינג

אם העיגול של הרינג מצוי כולו בתוך העקום $\gamma (\theta )$ אז המישור $PQ$ (שכיוונו: ${\overrightarrow {OP}}$) יופיע ב-ECS בנקודה $Q$. אם, לעומת זאת, חלק מעקום וולף חודר לתוך עיגול הרינג, אז המישור שכיוונו ${\overrightarrow {OP}}$ אינו קיים ב-ECS בנקודה $Q$.

צורת שיווי המשקל של הגביש היא, אם כן, המקום הגיאומטרי של כל הנקודות $Q$ על הכדורים המשיקים שאינם נחתכים על ידי חלקים אחרים של עקום $\gamma (\theta )$.

הוכחה

נניח שהעיגול של הרינג מצוי כולו בתוך העקום $\gamma (\theta )$ (חלק א' באיור). עבור כל נקודה $R$ על עקום $\gamma (\theta )$, שונה מ-$P$, חייבת להימצא נקודה אחרת כלשהי, $S$ בין $R$ ו-$O$, שנמצאת על העיגול המשיק, כך ש‑$\angle OSQ=90^{\circ }$. המישור המקביל ל-$SQ$ והעובר ב-$R$ (כלומר המשיק ל-$\gamma (\theta )$ ב-$R$) חייב לחתוך את הכיוון ${\overrightarrow {OQ}}$ מחוץ לעיגול המשיק. זאת אומרת, רחוק יותר מהראשית מאשר המשיק $PQ$. לכן, בכיוון ${\overrightarrow {OQ}}$ המשיק $PQ$ ל-$\gamma (\theta )$ נמצא על המעטפת הפנימית של המשיקים ל-$\gamma (\theta )$, ומכאן שהוא מצוי ב-ECS.

כעת נניח שחלק מעקום וולף $\gamma (\theta )$ חודר לתוך עיגול הרינג (חלק ב' באיור). במקרה כזה קיימת לפחות נקודה אחת על עקום וולף, למשל הנקודה $T$, שמצויה בין $O$ ובין נקודה אחרת $U$ שעל העיגול המשיק. כעת $\angle OUQ=90^{\circ }$ (כי היא נשענת על קוטר). הישר העובר דרך $T$ ומקביל ל-${U}Q$ הוא המשיק ל-$\gamma (\theta )$ ב-$T$. הוא חותך את $OQ$ בנקודה $Q'$ בתוך העיגול. כלומר, קרוב יותר לראשית בכיוון ${\overrightarrow {OQ}}$ מאשר המשיק ל-$\gamma (\theta )$ ב-$P$. לכן, המישור $PQ$ אינו יכול להיות חלק מהמעטפת הפנימית של המשיקים, ולא יימצא ב-ECS.

צורות שיווי המשקל של המקרים א' ו-ב' מוראות בכחול ב-ג' ו-ד', בהתאמה.

התלות בטמפרטורה של צורת שיווי-המשקל של הגביש - טמפרטורת חספוס

תיאור סכמתי של ההתחספסות של גביש של מלח בישול בטמפרטורה גבוהה. האיור מתאר שמינית של הגביש בשתי טמפרטורות שונות. בטמפרטורה הנמוכה (משמאל) לגביש צורת קובייה. בטמפרטורה הגבוהה (מימין) התחילה התחספסות בצלעות ובקודקוד שלה (האזורים שבתוך הצורה המעוגלת בכחול בהיר קמורים).

האנרגיה החופשית המשטחית הספציפית תלויה בטמפרטורה, ולכן עקום וולף וצורת שיווי המשקל של הגביש משתנים עם הטמפרטורה. תופעה מעניינת הקשורה בכך היא מעבר החספוס (roughening transition). מעבר זה מאופיין בהיעלמות הפאות בצורת שיווי המשקל של הגביש, כאשר הטמפרטורה עולה מגיעה לערך מסוים, הקרוי טמפרטורת החספוס. בטמפרטורות נמוכות מטמפרטורת מעבר זו מתחילות להופיע פאות בצורת הגביש, אבל ישנם בה אזורים מעוגלים (מחוספסים), קמורים. אזורי החספוס הללו הולכים וקטנים עם הורדת הטמפרטורה, עד שבסופו של דבר יופיעו בצורה צלעות וקודקודים. זה מודגם סכמתית באיור עבור המקרה של גבישים של מלח בישול. בטמפרטורה נמוכה מ-620 מעלות צלזיוס יש לגבישים הללו את צורת הקובייה האופיינית להם. זה מתאים, בהצגה דו-ממדית, ל-ECS ולעקום וולף שבחלק ד' של האיור למעלה. ב-650 מעלות מתחילים להתעגל הקודקודים של הקובייה, ובטמפרטורה גבוהה יותר גם הצלעות, כמוראה באיור עבור 700 מעלות בערך. מצב זה מתאים ל-ECS ולעקום וולף שבחלק ג' באיור למעלה. ההתעגלות (החספוס) של כיוונים מסוימים בגביש נובעת מכך שעם העלאת הטמפרטורה גדלות האנרגיות החופשיות המשטחיות הספציפיות בגלל תרומת האיבר האנטרופי לאנרגיה החופשית. כתוצאה מכך החודים בעקום וולף בולטים פחות (פנימה) וצורת העקום מתעגלת (השוו, באיור למעלה, בין עקום וולף בחלק ב' - טמפרטורה נמוכה, והעקום בחלק א' - טמפרטורה גבוהה).

שימוש ב-ECS לקביעת אנרגיות משטחיות ספציפיות

צריך לשים לב שבדרך כלל הצורה של גבישים (בעיקר בטבע) אינה צורת שיווי המשקל שלהם. במקרים אלו הצורה של הגביש נקבעת על ידי שבירתו במישורים מסוימים, או ליטושו במישורים מסוימים, למשל בהכנת אבני חן כמו יהלומים; או על ידי קצב הגידול של המישורים השונים של הגביש. מעשית, גבישים מגיעים לצורת שיווי המשקל שלהם אם האטומים יכולים לפעפע על פני השטח שלהם במהירות גבוהה מספיק כדי להגיע לאתרים המעודפים אנרגטית (כלומר שהאנרגיה החופשית שלהם מינימלית) על פני השטח. זה אפשרי, למשל, בגבישים קטנים של מתכות בטמפרטורות גבוהות מספיק.

כאשר גבישים מקבלים באמת את צורת שיווי המשקל שלהם, אפשר, תוך הסתמכות על משפט וולף, למדוד באמצעותה את האנרגיות המשטחיות של החומר בכיוונים השונים. זאת, אם ידועה, לפחות בכיוון אחד, האנרגיה המשטחית של החומר באותם תנאים. או, לכל הפחות, אפשר למצוא את היחסים בין האנרגיות המשטחיות הספציפיות של החומר בכיוונים השונים הקיימים ב-ECS. שכן, לפי משפט וולף, היחסים בין המרחקים לפאות ב-ECS ממרכזו שווים ליחסי האנרגיות המשטחיות הספציפיות בכיוונים אלו, וליחסים ההפוכים של שטחי הפאות: ${\gamma _{i} \over {\gamma }_{j}}={r_{i} \over {r}_{j}}={{A}_{j} \over {A}_{i}}$. במשוואה זו $A$ מציין את שטח הפאה, והאינדקסים $i,j$ מציינים את הכיוונים המתאימים בגביש.

בניית וולף קינטית

אף שמשפט וולף מתייחס לצורת הגבישים בשיווי משקל תרמודינמי, בעבודתו של וולף נעשו רוב התצפיות לגבי הגידול של גבישים, קרי המצב הקינטי ולא התרומדינמי. הוא אף ביטא זאת בשם המאמר שפרסם: על "השאלה של מהירות הגידול וההמסה של משטחים גבישיים". הוא הניח שקיים קשר ישיר בין האנרגיה החופשית של המישורים הגבישיים ובין קצב הגידול שלהם, אך זה לא תמיד המצב. כך התפתחה "בניית וולף קינטית" (kinetic Wulff construction), שבה מוחלפות האנרגיות המשטחיות הספציפיות עבור הכיוונים הגבישיים השונים במהירויות הגידול של הגביש בכיוונים אלו. גישה זו זוכה לתשומת לב רבה בפענוח וחיזוי הצורה של ננוחלקיקים חופשיים או על משטחים, וכן כאלו עם גבולות תאום. היא שימושית גם באפיטקסיה על מישורים גבישיים לא שכיחים.

קישורים חיצוניים

• S. Miracle-Sole, Wulff shape of crystals, Scholarpedia, ‏Retrieved October 23, 2023
• משפט וולף וצורת גביש בשיווי משקל, באתר MathWorld (באנגלית)