קואורדינטות קוטביות

מתוך ויקיפדיה, האנציקלופדיה החופשית

מערכות צירים וקואורדינטות

מערכות צירים נפוצות

ראו גם

מערכת קוארדינטות קוטבית. המעגלים הם $\ r=1, r=2, r=3$ . הקווים הישרים הם הקווים $\ \theta = 30^\circ,\ \theta=60^\circ$ וכן הלאה.

קואורדינטות קוטביות או קואורדינטות פולריות הן תיאור של המישור באמצעות שני משתנים:

r - המרחק מראשית הצירים.
θ - הזווית שיוצר הוקטור המחבר בין הנקודה לראשית הצירים, עם הכיוון החיובי של ציר ה-x.

קואורדינטות פולריות הן מקרה פרטי של קואורדינטות גליליות עבור גובה = 0, ומקרה פרטי של קואורדינטות כדוריות עבור זווית לטידיוד = 90 מעלות.

תוכן עניינים

1 המרה בין קואורדינטות פולריות לקואורדינטות קרטזיות
- 1.1 מציאת הזווית
2 וקטורי היחידה
3 קואורדינטות פולריות ומספרים מרוכבים
4 עקומות בקואורדינטות פולריות
5 ראו גם

[עריכה] המרה בין קואורדינטות פולריות לקואורדינטות קרטזיות

עבור נקודה כללית (x,y) ניתן להמיר לקואורדינטות פולריות על ידי

$\ r = \sqrt{x^2 + y^2}$

$\ \theta = \arctan{(y/x)}$ (להמרה מדויקת יותר, ראו בהמשך)

לחילופין, כאשר נתונים (r,θ) אפשר להמיר לקואורדינטות קרטזיות על ידי

$\ x = r \cos \theta$

$\ y = r \sin \theta$

[עריכה] מציאת הזווית

קל למצוא את הזווית באופן גרפי, אך חישובה באופן אלגברי מסובך יותר. ראשית, יש לקבוע איזה ערכים הזווית יכולה לקבל, כאשר עלינו לזכור שיש מחזוריות של $\ 2 \pi$ מכיוון ש-θ מייצגת זווית.

בדרך כלל בוחרים לעבוד באינטרוול [0, 2π), כלומר, הזווית מקבלת ערכים בין 0 ל-2π (לא כולל 2π). אזי ניתן למצוא את הזווית לפי הנוסחה הבאה:

$\ \theta = \begin{cases} \arctan(\frac{y}{x}) & \mbox{if } x > 0 \mbox{ and } y \ge 0\\ \arctan(\frac{y}{x}) + 2 \pi & \mbox{if } x > 0 \mbox{ and } y < 0\\ \arctan(\frac{y}{x}) + \pi & \mbox{if } x < 0\\ \frac{\pi}{2} & \mbox{if } x = 0 \mbox{ and } y > 0\\ \frac{3\pi}{2} & \mbox{if } x = 0 \mbox{ and } y < 0 \end{cases}$

כאשר arctan היא הפונקציה ההופכית לפונקציה הטריגונומטרית טנגנס.

אם עובדים באינטרוול (−π, π], יש להשתמש בנוסחה הבאה:

$\ \theta = \begin{cases} \arctan(\frac{y}{x}) & \mbox{if } x > 0\\ \arctan(\frac{y}{x}) + \pi & \mbox{if } x < 0 \mbox{ and } y \ge 0\\ \arctan(\frac{y}{x}) - \pi & \mbox{if } x < 0 \mbox{ and } y < 0\\ \frac{\pi}{2} & \mbox{if } x = 0 \mbox{ and } y > 0\\ -\frac{\pi}{2} & \mbox{if } x = 0 \mbox{ and } y < 0 \end{cases}$

[עריכה] וקטורי היחידה

בקואורדינטות קרטזיות אפשר לרשום את מיקומה של כל נקודה או וקטור כ

$\ \vec{A} = A_x \hat{e}_x + A_y \hat{e}_y + A_z \hat{e}_z = A_x \hat{x} + A_y \hat{y}$

כאשר $\ \hat{e}_i \ , \ i = \{ x, y \}$ הם וקטורי היחידה הקרטזיים (וקטורים אלה קבועים). באופן גאומטרי, וקטור היחידה x הוא וקטור הצביע בכיוון החיובי של ציר x ואורכו הוא 1 (ליתר דיוק נכון לומר שהנורמה שלו שווה ל 1), באותו אופן לגבי וקטורי היחידה בציר y.

אנו נרצה להציג באותה צורה את הנקודה שלנו גם בקואורדינטות פולריות:

$\ \vec{A} = A_r \hat{e}_r + A_\theta \hat{e}_\theta$

כאשר לוקטורים $\ \hat{e}_j \ , \ j = \{ r , \theta \}$ נקרא "וקטורי היחידה הפולריים".

אפשר לחשבם בכל נקודה במרחב ולקבל שהם נתונים על ידי

$\ \begin{matrix} \hat{r} = \hat{e}_r & = & ( \cos\theta ) \hat{x} & + ( \sin\theta) \hat{y} \\ \hat{\theta} = \hat{e}_\theta & = & ( - \sin\theta) \hat{x} & + ( \cos\theta ) \hat{y} \\ \end{matrix}$

כלומר: וקטורים אלה אינם קבועים במרחב, אלא כיוונם משתנה בהתאם לנקודה.

[עריכה] קואורדינטות פולריות ומספרים מרוכבים

איור של מספר מרוכב z המשורטט על המישור המרוכב

איור של מספר מרוכב המשורטט בעזרת נוסחת אוילר.

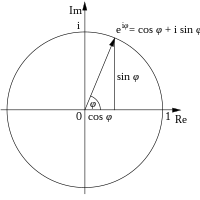
כל מספר מרוכב ניתן לייצג כנקודה במישור המרוכב ולכן ניתן לבטאו או באמצעות קואורדינטות קרטזיות

$\ z = x + i y$

או באמצעות קואורדינטות פולריות

$\ z = r \cos \theta + i r \sin \theta = r e^{i \theta}$

כאשר המעבר האחרון נעשה לפי נוסחת אוילר: $\ e^{i \theta} = \cos \theta + i \sin \theta$ והזווית נמדדת ברדיאנים.

באמצעות ההצגה הפולרית קל לבצע כפל, חילוק וחזקות של מספרים מרוכבים.

כפל:

$\ r_0 e^{i\theta_0} \cdot r_1 e^{i\theta_1}=r_0 r_1 e^{i(\theta_0 + \theta_1)} \,$

חילוק:

$\ \frac{r_0 e^{i\theta_0}}{r_1 e^{i\theta_1}}=\frac{r_0}{r_1}e^{i(\theta_0 - \theta_1)} \,$

חזקה (נוסחת דה-מואבר):

$\ (re^{i\theta})^n=r^ne^{in\theta} \,$

[עריכה] עקומות בקואורדינטות פולריות

המשוואה המגדירה עקומה אלגברית המבוטאת בקואורדינטות פולריות נקראת "משוואה פולרית" (Polar equation). במקרים רבים, ניתן לתארה בפשטות על ידי הגדרת $\ r$ כפונקציה של הזווית θ. העקומה המתקבלת מורכבת מנקודות מהצורה $\ \left( r \left( \theta \right), \theta \right)$ ואפשר להתייחס אליה כאל הגרף של הפונקציה הפולרית $\ r$ .

ניתן להסיק צורות שונות של סימטריה מהמשוואה של הפונקציה הפולרית $\ r$ . אם $\ r(\theta) = r(-\theta)$ אזי העקומה תהיה סימטרית סביב ציר-x (הקרן (0°/180°)). אם $\ r(\pi - \theta) = r(\theta)$ אזי העקומה תהיה סימטרית סביב ציר y (הקרן (90°/270°)). אם $\ r$ (θ−α°) = $\ r$ (θ) העקומה תהיה סימטרית סביב הציר בזווית °α כנגד כיוון השעון.

בגלל הטבע הציקלי-מעגלי של מערכת קואורדינטות פולריות, עקומות רבות ניתן לתאר באמצעות משוואה פולרית די פשוטה, כאשר הצורה הקרטזית היא הרבה יותר מסובכת. בין העקומות הידועות מסוג זה נמנות הספירלה הארכימדית, השושן הפולרי, הלמניסקייט של ברנולי, הלימצון והקרדיואיד.

עבור מעגל, קו ושושן פופולרי, אין הגבלה על התחום והטווח של העקומה.

[עריכה] מעגל

מעגל עם המשוואה $\ r(\theta) = 1$

המשוואה הכללית עבור מעגל שמרכזו נמצא ב( $\ r$ ₀, φ) ורדיוסו a היא

$\ r^2 - 2 r r_0 \cos(\theta - \varphi) + r_0^2 = a^2.\,$

ניתן לפשט משוואה זו עבור מקרים פרטיים, כמו למשל

$\ r(\theta)=a \,$

עבור מעגל בראשית הצרים ורדיוס a.

[עריכה] קו ישר

קווים ישרים רדיאלים שקורנים החוצה מראשית הצירים מיוצגים בידי המשוואה

$\ \theta = \varphi \,$ ,

כאשר φ היא זווית השיפוע של הקו (בנוסחה φ = arctan $\ m$ where $\ m$ כאשר m הוא השיפוע בקואורדינטות קרטזיות).

המשוואה של קו לא רדיאלי שניצב לקו הרדיאלי θ = φ בנקודה ( $\ r$ ₀, φ) היא

$\ r(\theta) = {r_0}\sec(\theta-\varphi). \,$

[עריכה] שושן פולרי

שושן פולרי עם המשוואה $\ r(\theta) = 2 \sin (4 \theta)$

שושן פולרי הוא עקומה מתמטית מפורסמת שנראית כמו עלי כותרת של פרח, וניתן לבטאה באמצעות משוואה פולרית פשוטה

$\ r(\theta) = a \cos (k\theta + \phi_0)\,$

לכל קבוע $\ \phi_0$ , כולל 0. אם k הוא מספר טבעי, המשוואה תיצור פרח עם k עלי כותרת כאשר k אי-זוגי ופרח עם 2k עלי כותרת כאשר k זוגי. אם k מספר רציונלי לא שלם, יווצר פרח דמוי ורד שבו עלי הכותרת חופפים זה את זה. יש לציין שהמשוואות לעולם לא מגדירות ורד עם 2, 6, 10, 14 וכו' עלי כותרת. המשתנה a מייצג את אורך עלי הכותרת של השושן.

[עריכה] ספירלת ארכימדס

זרוע אחת ספירלת ארכימדס של הממשוואה $\ r(\theta) = \theta$ עבור $\ 0 < \theta < 6 \pi$

הספירלה הארכימדית היא ספירלה מפורסמת שגולתה בידי ארכימדס, אותה ניתן לבטא באמצעות משוואה פולרית פשוטה. היא מתוארת על ידי המשוואה

$\ r(\theta) = a+b\theta. \,$

שינוי הפרמטר a יסובב את הספירלה ואילו שינוי הפרמטר b ישנה את המרחק בין הזרועות, שעבור ספירלה נתונה הוא תמיד קבוע. לספירלת ארכימדס יש 2 זרועות, אחת עבור θ > 0 ואחת עבור θ < 0. שני הזרועות מתחברות באופן חלק בחלק. לקיחת תמונת המראה של זרוע אחת מעבר לקו תיצור את הזרוע השנייה.

עקומה זו נחשבת לאחת העקומות החשובות שמבוטאת בפשטות רבה בזכות משוואה פולרית.

[עריכה] חתכי חרוט

ערך מורחב – חתכי חרוט

אליפסה, ומראה החצי לטוס-רקטום

חתך חרוטי עם מוקד אחד על ראשית הצירים והשני במקום אחר על הקרן 0° (כך שחצי הציר הראשי נמצא על ציר ה-x) מתוארת על ידי המשוואה

$\ r = { \ell\over {1 + e \cos \theta}}$

כאשר e היא האקסצנטריות ו- $\ \ell$ הוא חצי הלטוס רקטום (המרחק בציר y מהמוקד שנמצא על הציר הראשי אל העקומה). אם If e > 1, המשוואה מגדירה היפרבולה, אם if e = 1, היא מגדירה פרבולה, ואם e < 1 היא מגדירה אליפסה. המקרה הפרטי שבו e = 0 מגדיר מעגל עם רדיוס $\ \ell$ .

[עריכה] ראו גם

קואורדינטות קוטביות

מתוך ויקיפדיה, האנציקלופדיה החופשית

תוכן עניינים

[עריכה] המרה בין קואורדינטות פולריות לקואורדינטות קרטזיות

[עריכה] מציאת הזווית

[עריכה] וקטורי היחידה

[עריכה] קואורדינטות פולריות ומספרים מרוכבים

[עריכה] עקומות בקואורדינטות פולריות

[עריכה] מעגל

[עריכה] קו ישר

[עריכה] שושן פולרי

[עריכה] ספירלת ארכימדס

[עריכה] חתכי חרוט

[עריכה] ראו גם

צפיות

כלים אישיים

ניווט

קהילה

חיפוש

תיבת כלים

שפות אחרות